MATLAB | 我用MATLAB制作了一款伪3D第一视角迷宫小游戏

游戏效果

• 使用键盘上方向键↑向前移动
• 使用键盘左右方向键调整← →朝向

游戏原理说明

原理很简单，如效果图所示，主要就是以角色视角方向发射大量的直线模拟视线，并计算直线与墙壁交点，获取每一条视线方向下，角色到墙壁的距离，然后根据近大远小的原理绘制不同长度的竖向直线模拟墙壁。

第一代程序计算交点方法

第一代程序是使用的polyshape对象(二维多边形对象)制作墙壁，polyshape对象重载了函数intersect，可以直接求出直线与多边形的交集，程序编写更加简洁方便，给个检测直线和多边形交点的官方例子：

创建一个矩形多边形和一个线段：

poly1=polyshape([0 0 1 1],[1 0 0 1]);
lineseg=[-1 -1;1.5 1.5];

计算该多边形与线段的交集，并确定线段的哪些部分在多边形的内部，哪些在其外部。

[in,out] = intersect(poly1,lineseg);
plot(poly1)
hold on
plot(in(:,1),in(:,2),'b',out(:,1),out(:,2),'r')
legend('Polygon','Inside','Outside','Location','NorthWest')

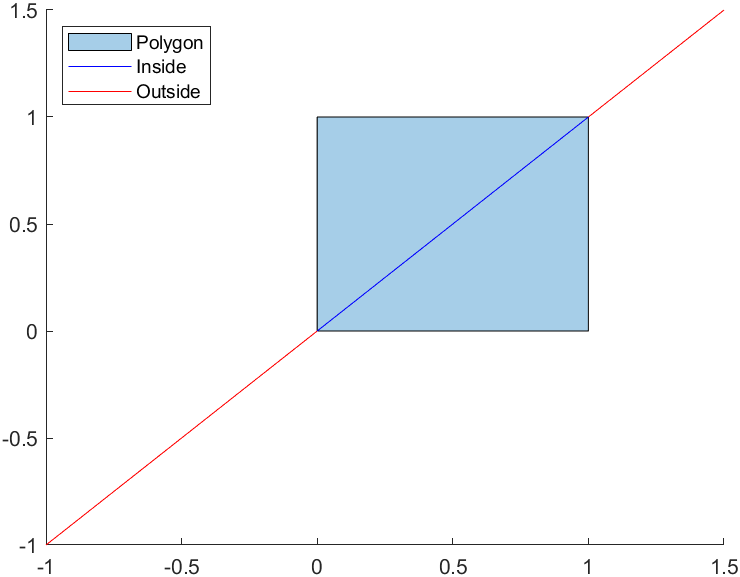
我们可以把内部第一个点和最后一个点看作与多边形边缘的交点：

intersectPnt=[in(1,:);in(end,:)]

intersectPnt = 0 0 1 1

但是！：这样的计算方法较缓慢，而且polyshape对象推出时间较晚(至少需要R2017B)， 于是该方案被舍弃！！ 于是该方案被舍弃！！ 于是该方案被舍弃！！

第二代程序计算交点方法

假设角色当前位置为 p 0 = ( x 0 , y 0 ) p_0=(x_0,y_0) p0​=(x0​,y0​)，角色当前面向方向为 θ 0 \theta_0 θ0​，将所有的墙壁边缘离散成点集合，其点到角色位置方向向量为： V = [ x 1 − x 0 y 1 − y 0 x 2 − x 0 y 2 − y 0 ⋮ ⋮ x N − x 0 y N − y 0 ] V=\left[\begin{array}{cc}x_1-x_0&y_1-y_0\\x_2-x_0&y_2-y_0\\\vdots&\vdots\\x_N-x_0&y_N-y_0\end{array}\right] V=⎣⎢⎢⎢⎡​x1​−x0​x2​−x0​⋮xN​−x0​​y1​−y0​y2​−y0​⋮yN​−y0​​⎦⎥⎥⎥⎤​

每个视线方向向量 T = [ cos ⁡ ( θ 1 + θ 0 ) sin ⁡ ( θ 1 + θ 0 ) cos ⁡ ( θ 2 + θ 0 ) sin ⁡ ( θ 3 + θ 0 ) ⋮ ⋮ cos ⁡ ( θ M + θ 0 ) sin ⁡ ( θ M + θ 0 ) ] T=\left[\begin{array}{cc}\cos(\theta_1+\theta_0)&\sin(\theta_1+\theta_0)\\\cos(\theta_2+\theta_0)&\sin(\theta_3+\theta_0)\\\vdots&\vdots\\\cos(\theta_M+\theta_0)&\sin(\theta_M+\theta_0)\end{array}\right] T=⎣⎢⎢⎢⎡​cos(θ1​+θ0​)cos(θ2​+θ0​)⋮cos(θM​+θ0​)​sin(θ1​+θ0​)sin(θ3​+θ0​)⋮sin(θM​+θ0​)​⎦⎥⎥⎥⎤​

做内积: I N N = V T ′ INN=VT' INN=VT′ 那么INN矩阵的每个数值都是角色到一个墙壁点方向向量与角色某一视线方向做内积，要考虑到视线为单方向射线，因此将内积为负数的值置为无穷大:INN(INN10)=10; PLINE.plotLine3(i).Color=[1,1,1]./10.*tLen; PLINE.plotLine3(i).YData=[5-tLen/2,5+tLen/2]; PLINE.plotLine2(i).XData=[RP.xpos,RP.xpos+cos(thetaList(i))*abs(minList(i))]; PLINE.plotLine2(i).YData=[RP.ypos,RP.ypos+sin(thetaList(i))*abs(minList(i))]; end end %% ======================================================================== % 数据旋转角度 function [X,Y]=rotateData(X,Y,theta) rotateMat=[cos(theta),-sin(theta);sin(theta),cos(theta)]; XY=rotateMat*[X;Y]; X=XY(1,:);Y=XY(2,:); end end

目前还没有加检测碰到墙的设置，所以是可以穿墙的，碰撞设置请自行编写，另外视角有点鱼眼的感觉是因为为了方便编写并没有考虑各个竖线的横向分布,如果考虑横向分布的话代码是这样的：

function maze2_5D_v3
% @author : slandarer
% @公众号 : slandarer随笔
% @知乎   : hikari
help maze2_5D_v3

%% ========================================================================
% figure窗口创建
fig=figure();
fig.Position=[50,60,1200,600];
fig.Name='maze 2.5D by slandarer';
fig.NumberTitle='off';
fig.MenuBar='none';
% 俯视图axes坐标区域
ax2D=axes('Parent',fig);
ax2D.XTick=[];ax2D.XColor='none';
ax2D.YTick=[];ax2D.YColor='none';
ax2D.XLim=[0,15];
ax2D.YLim=[0,15];
ax2D.Color=[0,0,0];
ax2D.Position=[0,0,1/2,1];
hold(ax2D,'on')
% 伪3D图axes坐标区域
ax3D=axes('Parent',fig);
ax3D.XTick=[];ax2D.XColor='none';
ax3D.YTick=[];ax2D.YColor='none';
ax3D.XLim=[0,10];
ax3D.YLim=[0,10];
ax3D.Color=[0,0,0];
ax3D.Position=[1/2,0,1/2,1];
hold(ax3D,'on')
%% ========================================================================
% 左侧俯视地图初始化
mazeMat=[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1;
         1 0 0 0 0 0 1 0 1 0 1 0 0 0 1;
         1 1 1 1 1 0 1 0 0 0 1 1 1 0 1;
         1 0 0 0 1 0 1 0 1 0 1 0 0 0 1;
         1 0 1 1 1 0 0 0 1 0 0 0 1 1 1;
         1 0 0 0 0 2 1 1 1 0 1 1 1 0 1;
         1 0 1 0 1 1 1 0 1 0 0 0 1 0 1;
         1 0 1 0 0 0 0 0 1 1 1 0 1 0 1;
         1 0 1 1 1 1 1 1 1 0 1 0 0 0 1;
         1 0 1 0 0 0 0 0 0 0 1 0 1 0 1;
         1 0 1 1 1 1 1 0 1 0 1 0 1 0 1;
         1 0 1 0 1 0 1 0 1 0 0 0 1 0 1;
         1 0 1 0 1 0 1 0 1 1 1 1 1 0 1;
         1 0 0 0 0 0 0 0 1 0 0 0 0 0 1;
         1 1 1 1 1 1 1 1 1 1 1 1 1 1 1];
[rowList,colList]=find(mazeMat==1);
sqX=[-1;0;0;-1];sqY=[-1;-1;0;0];
LSList=linspace(-1,0,250)';
NMList=-ones(size(LSList));
FLList=[[LSList,NMList];[LSList,NMList.*0];[NMList,LSList];[NMList.*0,LSList]];

BLOCK.pntSet=zeros(2,0);
for n=1:length(rowList) 
    fill(ax2D,sqX+colList(n),sqY+size(mazeMat,1)+1-rowList(n),[1,1,1].*0.9);
    BLOCK.pntSet=[BLOCK.pntSet;FLList+repmat([colList(n),size(mazeMat,1)+1-rowList(n)],[size(FLList,1),1])];
end
% -------------------------------------------------------------------------
% 角色创建
[trow,tcol]=find(mazeMat==2);
ROLEP.xpos=tcol-0.5;
ROLEP.ypos=size(mazeMat,1)+0.5-trow;
ROLEP.theta=pi/2;
ROLEP.triX=cos([pi/3,pi,-pi/3]).*0.15;
ROLEP.triY=sin([pi/3,pi,-pi/3]).*0.15;
[tX,tY]=rotateData(ROLEP.triX,ROLEP.triY,ROLEP.theta);
ROLEP.pfill=fill(ax2D,tX+ROLEP.xpos,tY+ROLEP.ypos,[1,1,1]);
ROLEP.pshape=polyshape(tX+ROLEP.xpos,tY+ROLEP.ypos);
ROLEP.viewRange=size(mazeMat,1)*sqrt(2);
%% ========================================================================
% 线条创建
% plot(ax3D,[1,1].*10.*i./length(thetaListV),[5-tLen/2,5+tLen/2],...
% 'LineWidth',1.5,'Color',[1,1,1]./10.*tLen,'Tag','blockLine');
% plot(ax2D,[RP.xpos,RP.xpos+cos(thetaList(i))*abs(minList(i))],[RP.ypos,RP.ypos+sin(thetaList(i))*abs(minList(i))])
lineNum=300;

ttV=linspace(pi/3,-pi/3,lineNum);
for n=1:lineNum
    PLINE.plotLine3(n)=plot(ax3D,-[1,1].*sin(ttV(n)).*10+5,[-1,-1],'LineWidth',3.5);
    PLINE.plotLine2(n)=plot(ax2D,[-1,-1],[-1,-1],'Color',lines(1));
end


draw3D(ROLEP,BLOCK,PLINE,lineNum)
%% ========================================================================
% 角色移动函数
set(fig,'KeyPressFcn',@key)
function key(~,event)
    %按键函数
    switch event.Key
        case 'uparrow'
            ROLEP.xpos=ROLEP.xpos+cos(ROLEP.theta).*.2;
            ROLEP.ypos=ROLEP.ypos+sin(ROLEP.theta).*.2;
        case 'leftarrow'
            ROLEP.theta=ROLEP.theta+pi/20;
        case 'rightarrow'
            ROLEP.theta=ROLEP.theta-pi/20;
    end
    [tX,tY]=rotateData(ROLEP.triX,ROLEP.triY,ROLEP.theta);
    ROLEP.pfill.XData=tX+ROLEP.xpos;
    ROLEP.pfill.YData=tY+ROLEP.ypos;
    ROLEP.pshape=polyshape(tX+ROLEP.xpos,tY+ROLEP.ypos);
    draw3D(ROLEP,BLOCK,PLINE,lineNum)
end
%% ========================================================================
% 视角检测及伪3D图绘制
    function draw3D(RP,BK,PLINE,LN)
    % delete(findobj('Tag','blockLine'))
    thetaListV=linspace(pi/3,-pi/3,LN);
    thetaList=thetaListV+RP.theta;
    % 内积法计算距离
    cutoff=1e-5;
    cosList=cos(thetaList);
    sinList=sin(thetaList);
    vecList=BK.pntSet-[RP.xpos,RP.ypos];
    disMat=vecList*[cosList;sinList];
    disMat(disMatcutoff)=inf;
    minList=min(abs(disMat));
    % 图像重绘
    for i=1:length(thetaList)
        tLen=10/abs(minList(i))/abs(cos(thetaListV(i))).*1;tLen(tLen>10)=10;
        PLINE.plotLine3(i).Color=[1,1,1]./10.*tLen;
        PLINE.plotLine3(i).YData=[5-tLen/2,5+tLen/2];
        PLINE.plotLine2(i).XData=[RP.xpos,RP.xpos+cos(thetaList(i))*abs(minList(i))];
        PLINE.plotLine2(i).YData=[RP.ypos,RP.ypos+sin(thetaList(i))*abs(minList(i))];
    end
end
%% ========================================================================
% 数据旋转角度
function [X,Y]=rotateData(X,Y,theta)
    rotateMat=[cos(theta),-sin(theta);sin(theta),cos(theta)];
    XY=rotateMat*[X;Y];
    X=XY(1,:);Y=XY(2,:);
end
end