MATLAB | MATLAB地形生成：矩形迭代法 · 傅里叶逆变换法 · 分形柏林噪声法

1:矩形迭代法

这个非常简单，就是将矩阵的四个角分别定下初值，之后进行如下形式的迭代就好： [ w x y z ] ⟶ [ w w + x 2 x w + y 2 w + x + y + z 4 x + z 2 y y + z 2 z ] + n o i s e . \begin{bmatrix} w& &x\\ & & \\ y& &z \end{bmatrix}\longrightarrow \begin{bmatrix} w&\frac{w+x}{2} &x\\ \frac{w+y}{2}& \frac{w+x+y+z}{4} &\frac{x+z}{2}\\ y&\frac{y+z}{2}&z \end{bmatrix}+\mathrm{noise}. ⎣ ⎡​wy​​xz​⎦ ⎤​⟶⎣ ⎡​w2w+y​y​2w+x​4w+x+y+z​2y+z​​x2x+z​z​⎦ ⎤​+noise. 迭代过程示意图：

此方法的迭代法来自公众号Aki君，的如下推送(点击下方图片跳转链接)，此迭代法程序已经写的非常简练，并没有什么优化的必要，可以去自行查看：

function B = land(A)
% @author :aki
% @公众号 :Aki君

N = size(A,1);
d = (N+1)/2;   % dimension
level = log2(N-1);           % noise
scalef = 0.05*(2^(0.9*level));     

B = A;
B(d,d) = mean([A(1,1),A(1,N),A(N,1)]) + scalef*randn;   
B(1,d) = mean([A(1,1),A(1,N)]) + scalef*randn;           
B(d,1) = mean([A(1,1),A(N,1)]) + scalef*randn;            
B(d,N) = mean([A(1,N),A(N,N)]) + scalef*randn;
B(N,d) = mean([A(N,1),A(N,N)]) + scalef*randn;

if N>3
    B(1:d,1:d) = land(B(1:d,1:d));
    B(1:d,d:N) = land(B(1:d,d:N));
    B(d:N,1:d) = land(B(d:N,1:d));
    B(d:N,d:N) = land(B(d:N,d:N));
end
end

但是，迭代运算毕竟不是MATLAB的强项，当矩阵尺度逐渐增大时，迭代法运算速度会变慢的很快，毕竟创建进程会非常多，因此在这补充一个循环法，只有核心代码只有十行，不过可能确实不如迭代法容易理解：

function A=sqLand(A)
% @author :slandarer
% @公众号 :slandarer随笔

% 获取矩阵大小 N=2^k+1
N=size(A,1);
tcyc=log2(N-1);
% 循环数值填充
for i=tcyc:-1:1
    s=2^(i-1);scalef=0.05*(2^(0.9*i));
    A(s+1:2*s:N,1:s:N)=(A(1:2*s:N-1,1:s:N)+A(2*s+1:2*s:N,1:s:N))/2;
    A(1:s:N,s+1:2*s:N)=(A(1:s:N,1:2*s:N-1)+A(1:s:N,2*s+1:2*s:N))/2;
    A(s+1:2*s:N,1:s:N)=A(s+1:2*s:N,1:s:N)+scalef.*randn(2^(tcyc-i),2^(tcyc-i+1)+1);
    A(1:2*s:N,s+1:2*s:N)=A(1:2*s:N,s+1:2*s:N)+scalef.*randn(2^(tcyc-i)+1,2^(tcyc-i));
end
end

不过虽然不易理解但速度确实是快了很多，做个测试哈：

k=2^11+1;
A=zeros(k);
A([1 k],[1 k])=[1,1.25;1.1,2.0];

tic
B1=land(A);
toc

tic
B2=sqLand(A);
toc

历时 8.315744 秒。 历时 0.098721 秒。

调用函数绘图：

k=2^5+1;
A=zeros(k);
A([1 k],[1 k]) = [1,1.25;1.1,2.0];
% B=land(A);
B=sqLand(A);

colormap('copper')
strCell={'FontSize',12,'FontName','Cambria'};
Bisland=max(B,mean(B));
Bmax=max(max(Bisland));
Bmin=min(min(Bisland));

subplot(221),meshz(B)
axis([0 k 0 k min(min(B)) Bmax])
title('Default view',strCell{:})

subplot(222), meshz(Bisland)
axis([0 k 0 k Bmin Bmax])
title('Default view',strCell{:})

subplot(223), meshz(Bisland)
view([-75,40])
axis([0 k 0 k Bmin Bmax])
title('view([-75 40])',strCell{:})

subplot(224), meshz(Bisland)
view([240 55])
axis([0 k 0 k Bmin Bmax])
title('view([240 55])',strCell{:})

2:傅里叶逆变换法

来自公众号好玩的MATLAB这篇推送，微调了一下代码(点击下方图片跳转链接)，其实就是生成满足一定条件的随机系数矩阵，再做个二维傅里叶逆变换就好：

X=linspace(0,1,200)';
CL=(-cos(X*2*pi)+1).^.2;
r=(X-.5)'.^2+(X-.5).^2;
surf(X,X',abs(ifftn(exp(7i*rand(a))./r.^.9)).*(CL*CL')*30)

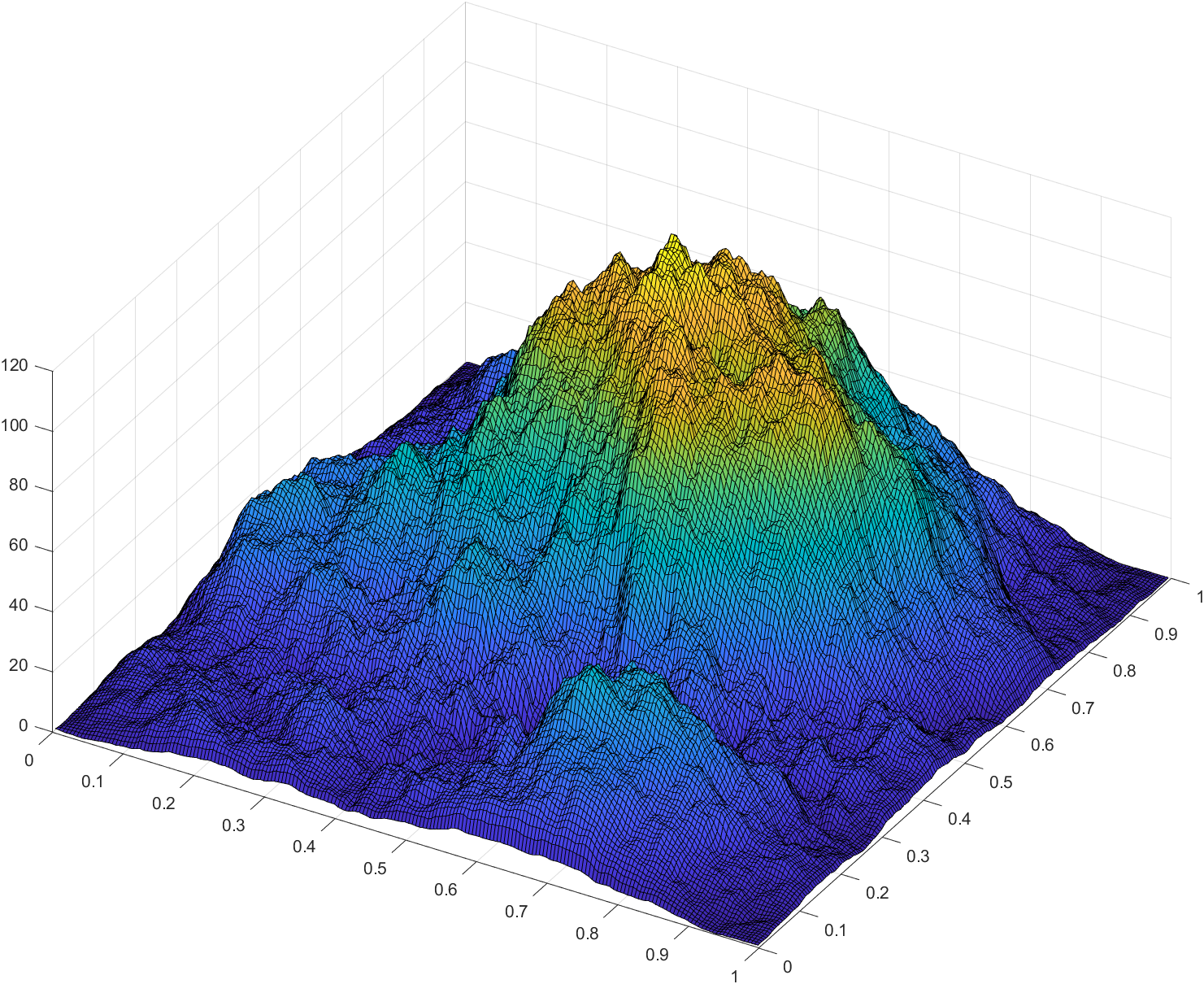不过该算法比较适合生成单体景观，比较难做成多山峰的大型连续景观。

分形柏林噪声法

首先构造基本网格，再构造细分网格，基本网格上每一格点上都含有一个梯度向量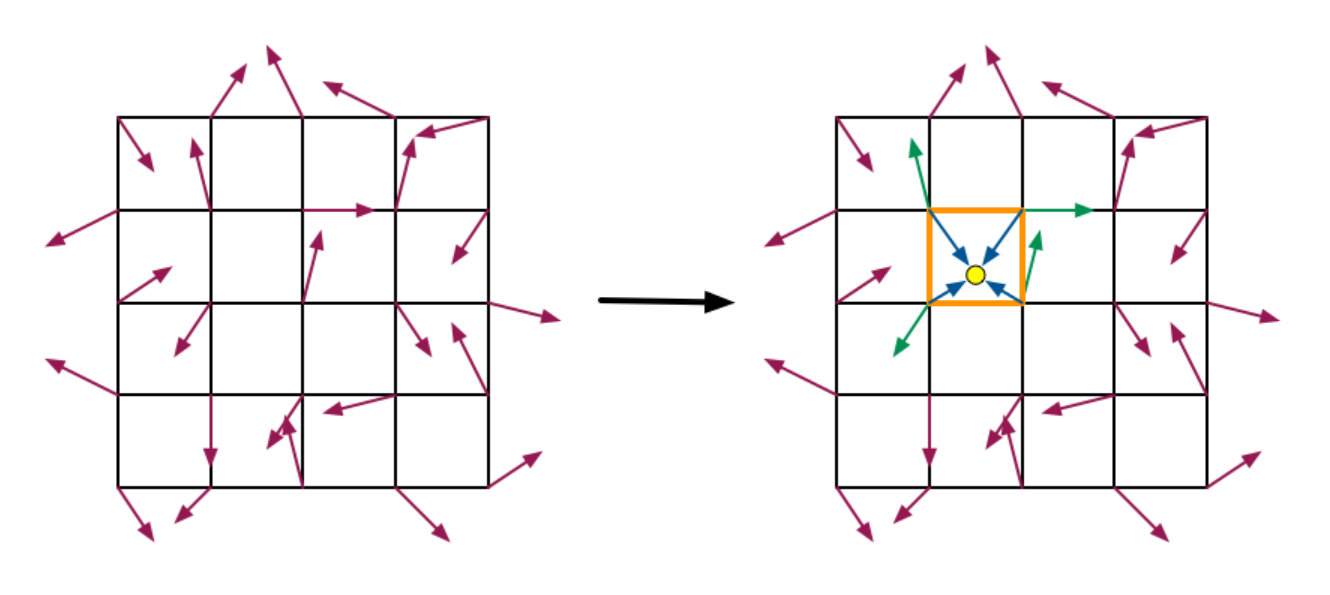： 细分网格上每一点都要与离其最近的四个基本网格上的梯度向量做内积。再将内积值乘以权重再相加即可获得噪声矩阵。

理论上这就是个二维插值，直接线性插值用上就完事：

但是，这样插值出来并不平滑，为了保证平滑性，我们需要将上述p,q值通过平滑的函数映射为其他值，常用的平滑函数有俩，一个是Smoothstep函数，此函数在x=0、x=0.5、x=1处分别等于0、0.5和1，0到1区间内整体也很平滑(f’(0)与f’(1)等于0)：

S m o o t h s t e p ( x ) = { 0 x ≤ 0 3 x 2 − 2 x 3 0 <   x < 1 1 x ≥ 0 \mathrm{Smoothstep} (x)=\left\{\begin{array}{ccc} 0 &x\le 0\\ 3x^{2}-2 x^{3} & 0