强化学习之SARSA

1. 准备内容 1.1 基于动态规划(DP)方法的强化学习 介绍

动态规划(DP)方法主要包含2个步骤：

• 策略评估 即给定任意一个策略 π ( a ∣ s ) \pi(a \mid s) π(a∣s)计算出对应的状态价值函数 V π ( s ) V_\pi(s) Vπ​(s)或状态-动作价值函数 q π ( s , a ) q_\pi(s,a) qπ​(s,a)
• 策略改进(策略迭代) 针对策略评估得到的价值函数 V π ( s ) V_\pi(s) Vπ​(s)、 q π ( s , a ) q_\pi(s,a) qπ​(s,a)使用贪心策略选择最优价值函数对应的策略 π ′ \pi^\prime π′,对上一时间点的策略 π \pi π进行迭代更新；

DP方法的迭代思路是贝尔曼期望方程： V k + 1 ( s ) = ∑ a ∈ A π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ R t + 1 + γ V k ( s ′ ) ] V_{k+1}(s)=\displaystyle\sum_{a\in A}\pi(a \mid s) \displaystyle\sum_{s^\prime,r}p(s^\prime,r\mid s,a)[R_{t+1}+\gamma V_k(s^\prime)] Vk+1​(s)=a∈A∑​π(a∣s)s′,r∑​p(s′,r∣s,a)[Rt+1​+γVk​(s′)]

贝尔曼期望方程本身属于不动点方程，满足不动点定理特性，根据不动点定理，(已被证明)该方程在迭代过程种产生的一系列结果 V ( S ) = [ V 1 ( s ) , V 2 ( s ) , . . . , V k ( s ) , V k + 1 ( s ) , . . . ] V(S)=[V_1(s),V_2(s),...,V_k(s),V_{k+1}(s),...] V(S)=[V1​(s),V2​(s),...,Vk​(s),Vk+1​(s),...]必然会收敛到最优解。

动态规划方法(DP)的局限性：

如果要使用DP方法进行策略改进，必要要提前知道动态特性函数 P ( s ′ , r ∣ s , a ) P(s^\prime,r \mid s,a) P(s′,r∣s,a)的具体结果，否则无法进行迭代计算；

1.2 基于蒙特卡洛(MC)方法的强化学习 介绍

MC的底层逻辑：大数定律 核心：通过对 G t G_t Gt​进行采样取均值以对某状态 s s s在策略 π \pi π的状态价值函数 V π ( s ) V_\pi(s) Vπ​(s)进行近似； G t G_t Gt​的计算公式如下： G t = R t + 1 + γ R t + 2 + γ 2 R T + 3 + . . . + γ T − 1 R t + T G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2R_{T+3} + ... + \gamma^{T-1}R_{t+T} Gt​=Rt+1​+γRt+2​+γ2RT+3​+...+γT−1Rt+T​ 数学符号表达： V π ( s ) = E π [ G t ∣ S t = s ] ≈ 1 N ∑ i = 1 N G t ( i ) V_\pi(s)=E_\pi[G_t \mid S_t=s] \approx\dfrac{1}{N}\displaystyle\sum_{i=1}^NG_t^{(i)} Vπ​(s)=Eπ​[Gt​∣St​=s]≈N1​i=1∑N​Gt(i)​

蒙特卡洛(MC)方法的局限性：

对 G t G_t Gt​采样的过程中，样本必须在一幕(从 t t t时刻开始， T T T时刻结束)全部执行结束的状态下，才能获取 R t + 1 , R t + 2 , . . . , R t + T R_{t+1},R_{t+2},...,R_{t+T} Rt+1​,Rt+2​,...,Rt+T​的具体结果，并最终获得1个 G t G_t Gt​结果；最终需要获取足够量的 G t G_t Gt​结果才能够执行均值操作，整个过程绝大部分时间浪费在了采样过程,时间利用率极低；

2. 基于MC的增量更新方式 2.1 增量更新和全量更新

以取均值为例： 已知一个数列中包含3个数值： [ 3 , 4 , 5 ] [3,4,5] [3,4,5] 使用全量更新的方法进行均值操作返回的结果： 3 + 4 + 5 3 = 4 \dfrac{3 + 4 + 5}{3} = 4 33+4+5​=4 使用增量更新的方法进行均值操作返回的结果：

• step 1 → \to → 输入第一个元素： 3 3 3，此时数列中只包含1个元素： [ 3 ] [3] [3]。当前均值结果： u 1 = 1 1 ∑ i = 1 1 x i = 3 u_1 = \frac{1}{1} \sum_{i=1}^1x_i = 3 u1​=11​i=1∑1​xi​=3
• step 2 → \to → 在step 1基础上，输入第二个元素： 4 4 4，此时数列中包含2个元素： [ 3 , 4 ] [3,4] [3,4]，当前均值结果计算如下： u 2 = 1 2 ∑ i = 1 2 x i = 3 + 4 2 = 3.5 u 2 = u 1 + 1 2 ( 4 − u 1 ) = 3 + 1 2 = 3.5 \begin{aligned} u_2 & = \frac{1}{2}\sum_{i=1}^2x_i = \frac{3 + 4}{2} = 3.5 \\ u_2 & = u_1 + \frac{1}{2}(4 - u_1) = 3 + \frac{1}{2} = 3.5 \end{aligned} u2​u2​​=21​i=1∑2​xi​=23+4​=3.5=u1​+21​(4−u1​)=3+21​=3.5​
• step 3 → \to → 在step 2基础上，输入第三个元素： 5 5 5,此时数列中包含3个元素： [ 3 , 4 , 5 ] [3,4,5] [3,4,5]，当前均值结果计算如下： u 3 = 1 3 ∑ i = 1 3 x i = 3 + 4 + 5 2 = 4 u 3 = u 2 + 1 3 ( 5 − u 2 ) = 3.5 + 1 2 = 4 \begin{aligned} u_3 & = \frac{1}{3}\sum_{i=1}^3x_i = \frac{3 + 4 +5}{2} = 4 \\ u_3 & = u_2 + \frac{1}{3}(5 - u_2) = 3.5 + \frac{1}{2} = 4 \end{aligned} u3​u3​​=31​i=1∑3​xi​=23+4+5​=4=u2​+31​(5−u2​)=3.5+21​=4​

2.2 基于MC的全量更新方法和增量更新方法

基于MC的增量更新方法作用公式如下：

V ( S t ) ← V ( S t ) + α ( G t − V ( S t ) ) ) V(S_t) \gets V(S_t) + \alpha(G_t - V(S_t))) V(St​)←V(St​)+α(Gt​−V(St​)))

解释： 全量更新方法相当于常规蒙特卡洛方法(MC)的学习方式： 若想要得到当前状态下的状态价值函数 V π ( s ) V_\pi(s) Vπ​(s)的近似结果 -> 需要采样采出若干个 G t G_t Gt​结果 -> 需要执行完若干个幕再执行均值操作才能实现(MC方法时间利用率低的局限性) 增量更新的方式： 每加入一个 G t G_t Gt​样本,就执行一次更新 -> 即便和真正的均值存在差异，但更新时间更短，更容易观察到收敛结果；

2.3 基于MC的增量更新方法的局限性

相比于常规MC全量更新的更新方法，增量更新方法有效提高了时间的利用率。但实际应用中，走1幕 -> 得到1个 G t G_t Gt​ -> 更新1次 V ( S t ) V(S_t) V(St​)这种更新方法的时间利用率仍然较低，希望能够找到比1个 G t G_t Gt​更小的单位对 V ( S t ) V(S_t) V(St​)进行更新。

3. 时序差分方法(Temporal Difference,TD)

时序差分作用公式： V ( S t ) ← V ( S t ) + α ( R t + 1 + γ V ( S t + 1 ) − V ( S t ) ) ) V(S_t) \gets V(S_t) + \alpha(R_{t+1} + \gamma V(S_{t+1}) - V(S_t))) V(St​)←V(St​)+α(Rt+1​+γV(St+1​)−V(St​))) 和基于MC的增量更新方法相比，TD方法将 G t G_t Gt​用贝尔曼期望方程的方式展开了； 这种方法的优势在于，相比于MC的增量方法，不需要将整个一幕走完，而是只需走一步( S t → S t + 1 S_t \to S_{t+1} St​→St+1​)即可执行一次状态价值函数 V ( S t ) V(S_t) V(St​)进行迭代。

该方法本质上将蒙特卡洛方法(MC)和动态规划方法(DP)相结合的思路

1. DP角度：该方法仍然是一个”自举“(Boostrapping)过程。

• 根据上个时间点状态的价值函数 V ( S t − 1 ) V(S_{t-1}) V(St−1​)的结果更新本时间点状态的价值函数信息 V ( S t ) V(S_t) V(St​)；
• 同理，下个时间点状态的价值函数结果 V ( S t + 1 ) V(S_{t+1}) V(St+1​)依赖本时间点状态的价值函数信息 V ( S t ) V(S_t) V(St​)；
• 时序差分方法的作用公式仍然是不动点方程。根据不动点定理，在迭代过程中所有状态对应的价值函数 V ( S ( 1 ) ) V(S^{(1)}) V(S(1)), V ( S ( 2 ) ) V(S^{(2)}) V(S(2)),…, V ( S ( m ) ) V(S^{(m)}) V(S(m))(m表示状态的数量，有多少种状态)都能收敛到最优结果。

2. MC角度：在步骤1参与迭代更新的过程中仍然在采样，只是之前MC方法采样的是 G t G_t Gt​，现在只是采样 R t + 1 R_{t+1} Rt+1​, V ( S t + 1 ) V(S_{t+1}) V(St+1​)。

上述过程中需要有行为(Action)的参与才能够执行策略改进； 接下来引入SARSA方法 -> 使用基于同轨方式的时序差分进行策略改进；

4. SARSA 4.1 SARSA作用公式

SARSA作用公式： Q ( S t , A t ) ← Q ( S t , A t ) + α ( R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ) Q(S_t,A_t) \gets Q(S_t,A_t) + \alpha (R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)) Q(St​,At​)←Q(St​,At​)+α(Rt+1​+γQ(St+1​,At+1​)−Q(St​,At​)) 该公式相比于时序差分的作用公式 -> 只是将 V ( S t ) → Q ( S t , A t ) V(S_t) \to Q(S_t,A_t) V(St​)→Q(St​,At​),但它的执行过程存在一些区别：

4.2 SARSA算法的执行过程

由于SARSA是基于同轨策略的时序差分控制 -> 需要行为策略必须是软策略 软策略 -> 当某行为 a a a在当前状态 s s s有意义的前提下，该行为发生的概率 >0恒成立，即该行为必然存在概率会发生。 数学符号表达： a ∈ A ( s ) → π ( a ∣ s ) > 0 a \in A(s) \to \pi(a \mid s)>0 a∈A(s)→π(a∣s)>0 具体执行过程如下：

• 使用 ϵ \epsilon ϵ-贪心方法(针对软策略 π ( a ∣ s ) \pi(a \mid s) π(a∣s))在 S t S_t St​状态下从满足条件的行为集合中选择一个行为 A t A_t At​ ；
• 选择完 A t A_t At​后，执行 A t A_t At​，系统必然将状态从 S t S_t St​状态更新到 S t + 1 S_{t+1} St+1​状态，并得到回馈结果 R t + 1 R_{t+1} Rt+1​;
• 再次使用策略 π ( a ∣ s ) \pi(a \mid s) π(a∣s)在 S t + 1 S_{t+1} St+1​状态下选择动作 A t + 1 A_{t+1} At+1​(该动作的选择方式同样是 ϵ \epsilon ϵ-贪心方法)，但不执行；而是通过 A t + 1 A_{t+1} At+1​和 S t + 1 S_{t+1} St+1​计算 Q ( S t + 1 , A t + 1 ) Q(S_{t+1},A_{t+1}) Q(St+1​,At+1​);
• 将3中的结果对 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)进行迭代： Q ( S t , A t ) ← Q ( S t , A t ) + α ( R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ) Q(S_t,A_t) \gets Q(S_t,A_t) + \alpha (R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)) Q(St​,At​)←Q(St​,At​)+α(Rt+1​+γQ(St+1​,At+1​)−Q(St​,At​))
• 将更新完的 Q ( S t , A t ) Q(S_t,A_t) Q(St​,At​)中选出一个最优Action -> A ∗ A^* A∗,使得： A ∗ = a r g m a x a Q ( S t , A t )    ⟺    Q ( S t , A ∗ ) = m a x Q ( S t , A t ) A^*= \underset {a}{argmax}Q(S_t,A_t)\iff Q(S_t,A^*)=maxQ(S_t,A_t) A∗=aargmax​Q(St​,At​)⟺Q(St​,A∗)=maxQ(St​,At​)
• 最后将 A ∗ A^* A∗使用 ϵ \epsilon ϵ-贪心方法对 π ( a ∣ s ) \pi(a \mid s) π(a∣s)进行迭代，算法结束；

注意：上述步骤只是更新了t时刻的状态St下各行为对应的概率分布，其他状态行为的概率分布没有变化； 执行过程分析：

1. π ( a ∣ s ) \pi(a \mid s) π(a∣s)是如何更新的； 通过 Q ( S t , A ∗ ) Q(S_t,A^*) Q(St​,A∗)获取最大值的行为 A ∗ A^* A∗通过 ϵ \epsilon ϵ-贪心方法对 π ( a ∣ s ) \pi(a \mid s) π(a∣s)进行迭代(程序开始时需要出始化 π ( a ∣ s ) \pi(a \mid s) π(a∣s))
2. 状态-动作价值函数是1个2维表格( Q t a b l e Q_{table} Qtable​) -> 每走一步，状态-动作价值函数和策略均会更新一次；

5.从代码角度认识SARSA

代码链接 具体了解一下代码任务 -> 机器人在不同位置下的路径选择问题； 共包含6个位置点(6种State)(离散型随机变量) -> 0,1,2,3,4,5; 共包含6种行为(Action)(离散型随机变量) -> 0,1,2,3,4,5（朝着0,1,2,3,4,5位置去） 回馈(Reward)(离散型随机变量) -> 三种情况[-1,0,100] 不同回馈情况表示的信息如下： -1 表示2个位置之间没有通路； 0 表示2个位置之间存在通路； 100 表示2个位置之间存在通路，并指向终点； 将回馈矩阵进行绘图，如下图所示： 绿色线表示回馈 -> 0 红色线表示回馈 -> 100 蓝色线表示回馈 -> -1 任务是在不同的位置点 -> 走向终点的路径 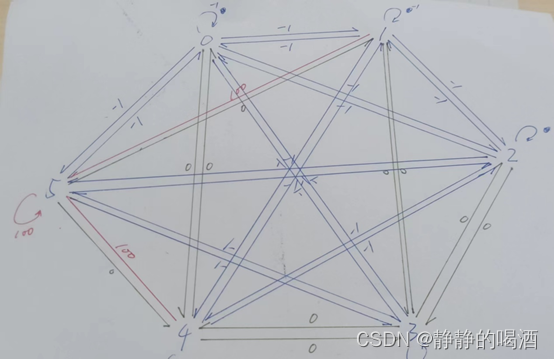代码及代码分析如下：

import numpy as np
import random

# get Q_table:
# 创建并初始化Q_table
Q_table = np.zeros((6,6))
Q_table = np.matrix(Q_table)

# get reward_table:
# 创建回馈矩阵(6*6)
r = np.array([[-1, -1, -1, -1, 0, -1], 
			[-1, -1, -1, 0, -1, 100], 
			[-1, -1, -1, 0, -1, -1], 
			[-1, 0, 0, -1, 0, -1],
            [0, -1, -1, 0, -1, 100], 
            [-1, 0, -1, -1, 0, 100]])
r = np.matrix(r)

#Q(S_t,A_t )←Q(S_t,A_t )+α(R_(t+1)+γQ(S_(t+1),A_(t+1) )-Q(S_t,A_t ))
# γ超参数-> 增量更新的变化量；
gamma = 0.8

# train_opera:
for i in range(2000):
    # 随机选取其中一个位置(状态)：
    state = random.randint(0,5)
    if state == 5:
        # print("The robot is at the end..")
        pass
    # 随机到5状态意味着直接到达终点，没有任何操作必要；
    while state != 5:
    	# 注意该位置 -> 并不是所有的行为Action在该状态的策略中，需要将无效行为剔除(回馈结果=-1的行为属于无效行为)，将剩余满足条件行为使用软策略；
        actions = []
        for a in range(6):
            if r[state,a] >= 0:
                actions.append(a)
		
		# 由于该示例比较简单，并没有使用ε-贪心方法，而是直接将选择概率平均分给所有满足条件的行为；
		# random.randint -> 服从概率均匀分布策略；
        action = actions[random.randint(0,len(actions) - 1)]

        R = r[state,action]
        # 根据上述选择得到的行为Action -> 从之前的位置走到当前位置；
        next_state = action

		# 重复之前的动作-> 剔除无效行为；
        actions = []
        for a in range(6):
            if r[next_state,a] >= 0:
                actions.append(a)
		
		# 核心操作 -> 依旧使用random.randint概率平均策略(同轨策略)
		# 该策略和第一次选择Action时的策略完全相同
        next_action = actions[random.randint(0,len(actions) - 1)]
		
		# 执行SARSA迭代公式
        Q_table[state,action] = R + gamma * Q_table[next_state,next_action]
		
		# 更新状态
        state = next_state
        # 更新行为
        action = next_action

    print(Q_table)
    print("---" * 30)

    # test_opera:

    for i in range(20):
        # print("第{}次验证".format(i + 1))

        state = random.randint(0,5)
        # print("机器人处于{}状态".format(state))
        count = 0
        while state != 5:
            if count > 20:
                # print("fail")
                break
            # 选择最大的Q:
            q_max = Q_table[state].max()

            q_max_action = []
            for action in range(6):
                if Q_table[state,action] == q_max:
                    q_max_action.append(action)

            next_state = q_max_action[random.randint(0,len(q_max_action) - 1)]
            # print("机器人将去{}状态".format(str(next_state)))
            state = next_state
            count += 1

需要注意的点： 该代码中不存在策略更新的部分 -> random.randint在没有其他参数的情况下，就是概率平均分布并从中随机选择一个行为，无论怎么迭代都不会发生变化。