机器学习笔记之降维(二)样本均值与样本方差的矩阵表示

引言

上一节介绍了维数灾难，随着维数增加对计算量与样本稀疏性造成的影响。本节将介绍降维的预备知识——对样本均值和样本方差进行矩阵表示。

场景介绍

已知数据集合 X \mathcal X X由 N N N个样本构成： X = { x ( 1 ) , x ( 2 ) , ⋯   , x ( N ) } \mathcal X = \{x^{(1)},x^{(2)},\cdots,x^{(N)}\} X={x(1),x(2),⋯,x(N)} 任意样本 x ( i ) ( i = 1 , 2 , ⋯   , N ) x^{(i)}(i=1,2,\cdots,N) x(i)(i=1,2,⋯,N)均包含 p p p维特征： x ( i ) = ( x 1 ( i ) x 2 ( i ) ⋮ x p ( i ) ) x ( i ) ∈ R p , i = 1 , 2 , ⋯   , N x^{(i)} = \begin{pmatrix}x_1^{(i)} \\ x_2^{(i)} \\ \vdots \\ x_p^{(i)}\end{pmatrix} \quad x^{(i)} \in \mathbb R^p,i=1,2,\cdots,N x(i)=⎝ ⎛​x1(i)​x2(i)​⋮xp(i)​​⎠ ⎞​x(i)∈Rp,i=1,2,⋯,N 至此，数据集合 X \mathcal X X可表示为 N × p N \times p N×p的矩阵形式： X = ( x ( 1 ) , x ( 2 ) , ⋯   , x ( N ) ) T = ( x 1 ( 1 ) , x 2 ( 1 ) , ⋯   , x p ( 1 ) x 1 ( 2 ) , x 2 ( 2 ) , ⋯   , x p ( 2 ) ⋮ x 1 ( N ) , x 2 ( N ) , ⋯   , x p ( N ) ) N × p \mathcal X = \begin{pmatrix}x^{(1)},x^{(2)},\cdots,x^{(N)}\end{pmatrix}^{T} = \begin{pmatrix} x_1^{(1)},x_2^{(1)},\cdots,x_p^{(1)} \\ x_1^{(2)},x_2^{(2)},\cdots,x_p^{(2)} \\ \vdots \\ x_1^{(N)},x_2^{(N)},\cdots,x_p^{(N)}\end{pmatrix}_{N \times p} X=(x(1),x(2),⋯,x(N)​)T=⎝ ⎛​x1(1)​,x2(1)​,⋯,xp(1)​x1(2)​,x2(2)​,⋯,xp(2)​⋮x1(N)​,x2(N)​,⋯,xp(N)​​⎠ ⎞​N×p​

样本均值与样本方差

假设数据集合 X \mathcal X X是 一维数据集合：

• 其样本均值(Sample Mean) X ˉ \bar {\mathcal X} Xˉ表示具体如下： X ˉ = 1 N ∑ i = 1 N x ( i ) \bar {\mathcal X} = \frac{1}{N} \sum_{i=1}^{N} x^{(i)} Xˉ=N1​i=1∑N​x(i)
• 样本方差(Sample Convariance) S \mathcal S S具体表示如下： S = 1 N ∑ i = 1 N ( x ( i ) − X ˉ ) 2 \mathcal S = \frac{1}{N} \sum_{i=1}^N (x^{(i)} - \bar{\mathcal X})^2 S=N1​i=1∑N​(x(i)−Xˉ)2

对应地，如果数据集合 X \mathcal X X中的样本 x ( i ) ( i = 1 , 2 , ⋯   , N ) x^{(i)}(i=1,2,\cdots,N) x(i)(i=1,2,⋯,N)是 p p p维向量。这样一个集合，它的 样本均值和样本方差如何表示呢？

• 样本均值： X ˉ = 1 N ∑ i = 1 N x ( i ) \bar {\mathcal X} = \frac{1}{N} \sum_{i=1}^{N} x^{(i)} Xˉ=N1​i=1∑N​x(i)

• 样本方差： S = 1 N ∑ i = 1 N ( x ( i ) − X ˉ ) ( x ( i ) − X ˉ ) T \mathcal S = \frac{1}{N} \sum_{i=1}^N (x^{(i)} - \bar {\mathcal X})(x^{(i)} - \bar {\mathcal X})^{T} S=N1​i=1∑N​(x(i)−Xˉ)(x(i)−Xˉ)T

由于 x ( i ) x^{(i)} x(i)是一个 p p p维向量，因而样本均值 X ˉ \bar {\mathcal X} Xˉ同样是一个 p p p维向量形式： X ˉ = ( 1 N ∑ i = 1 N x 1 ( i ) 1 N ∑ i = 1 N x 2 ( i ) ⋮ 1 N ∑ i = 1 N x p ( i ) ) p × 1 \bar {\mathcal X} = \begin{pmatrix} \frac{1}{N} \sum_{i=1}^{N} x_1^{(i)} \\ \frac{1}{N} \sum_{i=1}^{N} x_2^{(i)} \\ \vdots \\ \frac{1}{N} \sum_{i=1}^{N} x_p^{(i)}\end{pmatrix}_{p \times 1} Xˉ=⎝ ⎛​N1​∑i=1N​x1(i)​N1​∑i=1N​x2(i)​⋮N1​∑i=1N​xp(i)​​⎠ ⎞​p×1​

对应的样本方差是一个 p × p p\times p p×p的方阵形式： S p × p = 1 N ∑ i = 1 N ( x ( i ) − X ˉ ) p × 1 ⋅ ( x ( i ) − X ˉ ) 1 × p T \mathcal S_{p \times p} = \frac{1}{N} \sum_{i=1}^N (x^{(i)} - \bar {\mathcal X})_{p \times 1} \cdot (x^{(i)} - \bar {\mathcal X})_{1 \times p}^{T} Sp×p​=N1​i=1∑N​(x(i)−Xˉ)p×1​⋅(x(i)−Xˉ)1×pT​

样本均值与样本方差的矩阵表示 样本均值的矩阵表达

将样本均值公式展开，写成如下向量乘法形式： X ˉ = 1 N ∑ i = 1 N x ( i ) = 1 N ( x ( 1 ) , x ( 2 ) , ⋯   , x ( N ) ) p × N ⋅ ( 1 1 ⋮ 1 ) N × 1 \bar {\mathcal X} = \frac{1}{N} \sum_{i=1}^N x^{(i)} = \frac{1}{N}\begin{pmatrix}x^{(1)},x^{(2)},\cdots,x^{(N)}\end{pmatrix}_{p \times N} \cdot \begin{pmatrix}1 \\ 1\\ \vdots \\1\end{pmatrix}_{N \times 1} Xˉ=N1​i=1∑N​x(i)=N1​(x(1),x(2),⋯,x(N)​)p×N​⋅⎝ ⎛​11⋮1​⎠ ⎞​N×1​ 定义如下符号： 元素均为1的 N N N维列向量。 ( 1 1 ⋮ 1 ) N × 1 = I N \begin{pmatrix}1 \\ 1\\ \vdots \\1\end{pmatrix}_{N \times 1} = \mathcal I_N ⎝ ⎛​11⋮1​⎠ ⎞​N×1​=IN​ 样本均值 X ˉ \bar {\mathcal X} Xˉ可表示为如下形式： X ˉ = 1 N ( x ( 1 ) , x ( 2 ) , ⋯   , x ( N ) ) ⋅ I N = 1 N X T ⋅ I N \begin{aligned} \bar{\mathcal X} & = \frac{1}{N} \begin{pmatrix}x^{(1)},x^{(2)},\cdots,x^{(N)}\end{pmatrix} \cdot \mathcal I_N \\ & = \frac{1}{N} \mathcal X^{T} \cdot \mathcal I_N \end{aligned} Xˉ​=N1​(x(1),x(2),⋯,x(N)​)⋅IN​=N1​XT⋅IN​​

样本方差的矩阵表达

同样本均值，将样本方差公式进行展开： S = 1 N ∑ i = 1 N ( x ( i ) − X ˉ ) ( x ( i ) − X ˉ ) T = 1 N [ ( x ( 1 ) − X ˉ ) ( x ( 1 ) − X ˉ ) T + ⋯ + ( x ( N ) − X ˉ ) ( x ( N ) − X ˉ ) T ] \begin{aligned} \mathcal S & = \frac{1}{N} \sum_{i=1}^N (x^{(i)} - \bar {\mathcal X})(x^{(i)} - \bar {\mathcal X})^{T} \\ & = \frac{1}{N} \left[ (x^{(1)} - \bar{\mathcal X})(x^{(1)} - \bar{\mathcal X})^{T} + \cdots + (x^{(N)} - \bar{\mathcal X})(x^{(N)} - \bar{\mathcal X})^{T}\right] \end{aligned} S​=N1​i=1∑N​(x(i)−Xˉ)(x(i)−Xˉ)T=N1​[(x(1)−Xˉ)(x(1)−Xˉ)T+⋯+(x(N)−Xˉ)(x(N)−Xˉ)T]​ 将上述中括号中的元素表示为向量乘积的形式： S = 1 N ( x ( 1 ) − X ˉ , ⋯   , x ( N ) − X ˉ ) ⋅ [ ( x ( 1 ) − X ˉ ) T ( x ( 2 ) − X ˉ ) T ⋮ ( x ( N ) − X ˉ ) T ] \mathcal S = \frac{1}{N} \left(x^{(1)} - \bar {\mathcal X} , \cdots, x^{(N)} - \bar{\mathcal X}\right) \cdot \begin{bmatrix} \left(x^{(1)} - \bar {\mathcal X}\right)^{T} \\ \left(x^{(2)} - \bar {\mathcal X}\right)^{T} \\ \vdots \\ \left(x^{(N)} - \bar {\mathcal X}\right)^{T}\end{bmatrix} S=N1​(x(1)−Xˉ,⋯,x(N)−Xˉ)⋅⎣ ⎡​(x(1)−Xˉ)T(x(2)−Xˉ)T⋮(x(N)−Xˉ)T​⎦ ⎤​ 其中， ( x ( 1 ) − X ˉ , ⋯   , x ( N ) − X ˉ ) \left(x^{(1)} - \bar {\mathcal X} , \cdots, x^{(N)} - \bar{\mathcal X}\right) (x(1)−Xˉ,⋯,x(N)−Xˉ)可拆成两个行向量的差值： ( x ( 1 ) − X ˉ , ⋯   , x ( N ) − X ˉ ) = ( x ( 1 ) , ⋯   , x ( N ) ) − ( X ˉ , ⋯   , X ˉ ) = X T − X ˉ ⋅ ( 1 , 1 , ⋯   , 1 ) 1 × N = X T − X ˉ ⋅ I N T \begin{aligned} \left(x^{(1)} - \bar {\mathcal X} , \cdots, x^{(N)} - \bar{\mathcal X}\right) & = \left(x^{(1)}, \cdots ,x^{(N)}\right) - \left(\bar {\mathcal X},\cdots, \bar {\mathcal X}\right) \\ & = \mathcal X^{T} - \bar {\mathcal X} \cdot (1,1, \cdots,1)_{1 \times N} \\ & = \mathcal X^{T} - \bar {\mathcal X} \cdot \mathcal I_N^{T} \end{aligned} (x(1)−Xˉ,⋯,x(N)−Xˉ)​=(x(1),⋯,x(N))−(Xˉ,⋯,Xˉ)=XT−Xˉ⋅(1,1,⋯,1)1×N​=XT−Xˉ⋅INT​​ 将样本均值 X ˉ \bar {\mathcal X} Xˉ的矩阵表示结果代入上式，并将 X T \mathcal X^{T} XT提出来： 注意该位置提取公因式的时候, X T \mathcal X^{T} XT对应的公因式结果是 E N \mathcal E_N EN​而不是单纯的1。其中 E N \mathcal E_N EN​是N维单位矩阵。即： X T E N = X T \mathcal X^{T}\mathcal E_N = \mathcal X^{T} XTEN​=XT

X T − 1 N X T ⋅ I N ⋅ I N T = X T ( E N − 1 N I N I N T ) \mathcal X^{T} - \frac{1}{N} \mathcal X^{T}\cdot \mathcal I_N \cdot \mathcal I_N^{T} = \mathcal X^{T} \left(\mathcal E_N - \frac{1}{N} \mathcal I_N\mathcal I_N^{T}\right) XT−N1​XT⋅IN​⋅INT​=XT(EN​−N1​IN​INT​)

由于 [ ( x ( 1 ) − X ˉ ) T ( x ( 2 ) − X ˉ ) T ⋮ ( x ( N ) − X ˉ ) T ] \begin{bmatrix} \left(x^{(1)} - \bar {\mathcal X}\right)^{T} \\ \left(x^{(2)} - \bar {\mathcal X}\right)^{T} \\ \vdots \\ \left(x^{(N)} - \bar {\mathcal X}\right)^{T}\end{bmatrix} ⎣ ⎡​(x(1)−Xˉ)T(x(2)−Xˉ)T⋮(x(N)−Xˉ)T​⎦ ⎤​是 ( x ( 1 ) − X ˉ , ⋯   , x ( N ) − X ˉ ) \left(x^{(1)} - \bar {\mathcal X} , \cdots, x^{(N)} - \bar{\mathcal X}\right) (x(1)−Xˉ,⋯,x(N)−Xˉ)的转置形式，则有： [ ( x ( 1 ) − X ˉ ) T ( x ( 2 ) − X ˉ ) T ⋮ ( x ( N ) − X ˉ ) T ] = [ X T ( E N − 1 N I N I N T ) ] T = ( E N − 1 N I N I N T ) T ⋅ X \begin{bmatrix} \left(x^{(1)} - \bar {\mathcal X}\right)^{T} \\ \left(x^{(2)} - \bar {\mathcal X}\right)^{T} \\ \vdots \\ \left(x^{(N)} - \bar {\mathcal X}\right)^{T}\end{bmatrix} = \left[\mathcal X^{T} \left(\mathcal E_N - \frac{1}{N} \mathcal I_N\mathcal I_N^{T}\right)\right]^{T} = \left(\mathcal E_N - \frac{1}{N} \mathcal I_N\mathcal I_N^{T}\right)^{T} \cdot \mathcal X ⎣ ⎡​(x(1)−Xˉ)T(x(2)−Xˉ)T⋮(x(N)−Xˉ)T​⎦ ⎤​=[XT(EN​−N1​IN​INT​)]T=(EN​−N1​IN​INT​)T⋅X

至此，样本方差 S \mathcal S S的矩阵结果表示如下： S = 1 N X T ( E N − 1 N I N I N T ) ⋅ ( E N − 1 N I N I N T ) T ⋅ X \mathcal S = \frac{1}{N} \mathcal X^{T} (\mathcal E_N - \frac{1}{N} \mathcal I_N \mathcal I_N^{T}) \cdot (\mathcal E_N - \frac{1}{N} \mathcal I_N \mathcal I_N^{T})^{T} \cdot \mathcal X S=N1​XT(EN​−N1​IN​INT​)⋅(EN​−N1​IN​INT​)T⋅X

我们将 E N − 1 N I N I N T \mathcal E_N - \frac{1}{N} \mathcal I_N \mathcal I_N^{T} EN​−N1​IN​INT​称作中心矩阵(Centering Matrix)，用 H N \mathcal H_N HN​表示。至此，样本方差 S \mathcal S S的矩阵表示可化简为： S = 1 N X T H ⋅ H T X \mathcal S = \frac{1}{N} \mathcal X^{T} \mathcal H \cdot \mathcal H^{T} \mathcal X S=N1​XTH⋅HTX

中心矩阵的性质

中心矩阵的物理意义相当于对样本空间中的样本点进行平移，平移至样本空间的原点位置。

示例： 已知 K \mathcal K K是由两个2维样本组成的样本集合，具体表示如下： K = ( 1 2 3 4 ) \mathcal K = \begin{pmatrix} 1 \quad 2 \\ 3 \quad 4 \end{pmatrix} K=(1234​) 此时，数据集合中仅包含两个样本： A : ( 1 , 3 ) \mathcal A:(1,3) A:(1,3)， B : ( 2 , 4 ) \mathcal B:(2,4) B:(2,4)。其对应的中心矩阵 H 2 \mathcal H_2 H2​表示如下： H 2 = E 2 − 1 2 I 2 ⋅ I 2 T = ( 1 0 0 1 ) − 1 2 ( 1 1 1 1 ) = ( 1 2 − 1 2 − 1 2 1 2 ) \begin{aligned} \mathcal H_2 & = \mathcal E_2 - \frac{1}{2} \mathcal I_2 \cdot \mathcal I_2^{T} \\ & = \begin{pmatrix}1 \quad 0 \\ 0 \quad 1\end{pmatrix} - \frac{1}{2}\begin{pmatrix}1 \quad 1 \\ 1 \quad 1\end{pmatrix} \\ & = \begin{pmatrix}\frac{1}{2} \quad -\frac{1}{2} \\ -\frac{1}{2} \quad \frac{1}{2}\end{pmatrix} \end{aligned} H2​​=E2​−21​I2​⋅I2T​=(1001​)−21​(1111​)=(21​−21​−21​21​​)​ 此时，样本 K \mathcal K K左乘中心矩阵 H 2 \mathcal H_2 H2​，具体结果如下： K ⋅ H 2 = ( − 1 2 1 2 − 1 2 1 2 ) \mathcal K \cdot \mathcal H_2 = \begin{pmatrix}-\frac{1}{2} \quad \frac{1}{2} \\ -\frac{1}{2} \quad \frac{1}{2}\end{pmatrix} K⋅H2​=(−21​21​−21​21​​) 此时得到两个新的样本点： A ′ : ( − 1 2 , − 1 2 ) \mathcal A':(-\frac{1}{2},-\frac{1}{2}) A′:(−21​,−21​)， B ′ : ( 1 2 , 1 2 ) \mathcal B':(\frac{1}{2},\frac{1}{2}) B′:(21​,21​)。原始样本点与新样本点在样本空间中的表示如下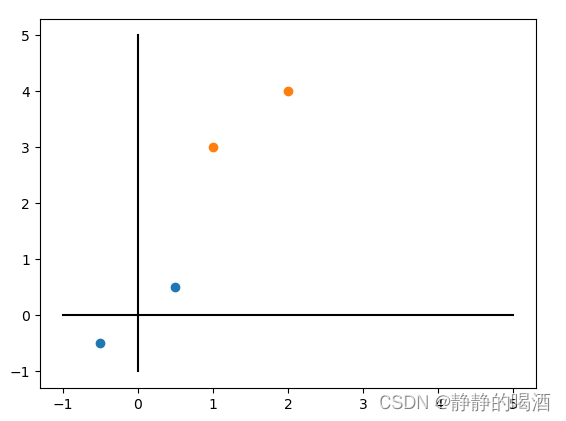： 其中橙色点是原始样本点；蓝色点是左乘中心矩阵后的新样本点。可以观察得到相比于原始样本点，新样本点向原点位置偏移，但样本点之间的相对位置没有变化。

观察中心矩阵 H \mathcal H H： H N × N = E N − 1 N I N I N T \mathcal H_{N \times N} = \mathcal E_N - \frac{1}{N} \mathcal I_N\mathcal I_N^{T} HN×N​=EN​−N1​IN​INT​

• 中心矩阵的转置 H T \mathcal H^{T} HT： 由于 E \mathcal E E是单位矩阵，因此有： E T = E \mathcal E^{T} = \mathcal E ET=E H T = ( E N − 1 N I N I N T ) T = ( E N ) T − 1 N ⋅ ( I N T ) T ⋅ I N T = E N − 1 N I N I N T = H \begin{aligned} \mathcal H^{T} & = (\mathcal E_N - \frac{1}{N} \mathcal I_N \mathcal I_N^{T})^{T} \\ & = (\mathcal E_N)^{T} - \frac{1}{N} \cdot (\mathcal I_N^{T})^{T} \cdot \mathcal I_N^{T} \\ & = \mathcal E_N - \frac{1}{N} \mathcal I_N \mathcal I_N^{T} \\ & = \mathcal H \end{aligned} HT​=(EN​−N1​IN​INT​)T=(EN​)T−N1​⋅(INT​)T⋅INT​=EN​−N1​IN​INT​=H​ 由此可知，中心矩阵 H \mathcal H H是一个对称矩阵；

• 中心矩阵的平方 H 2 \mathcal H^2 H2： H 2 = H ⋅ H = ( E N − 1 N I N I N T ) ⋅ ( E N − 1 N I N I N T ) = E N − 2 N I N I N T + 1 N 2 I N I N T ⋅ I N I N T \begin{aligned} \mathcal H^2 & = \mathcal H \cdot \mathcal H \\ & = (\mathcal E_N - \frac{1}{N} \mathcal I_N \mathcal I_N^{T})\cdot (\mathcal E_N - \frac{1}{N} \mathcal I_N \mathcal I_N^{T}) \\ & = \mathcal E_N - \frac{2}{N}\mathcal I_N\mathcal I_N^{T} + \frac{1}{N^2} \mathcal I_N\mathcal I_N^{T}\cdot \mathcal I_N\mathcal I_N^{T} \end{aligned} H2​=H⋅H=(EN​−N1​IN​INT​)⋅(EN​−N1​IN​INT​)=EN​−N2​IN​INT​+N21​IN​INT​⋅IN​INT​​ 因为 I N I N T \mathcal I_N\mathcal I_N^{T} IN​INT​它的结果是一个各元素均为1的 N × N N\times N N×N的方阵，因而 I N I N T ⋅ I N I N T \mathcal I_N\mathcal I_N^{T}\cdot \mathcal I_N\mathcal I_N^{T} IN​INT​⋅IN​INT​结果是一个各元素均为 N N N的 N × N N \times N N×N的方阵。即： I N I N T ⋅ I N I N T = N ⋅ I N I N T \mathcal I_N\mathcal I_N^{T}\cdot \mathcal I_N\mathcal I_N^{T} = N \cdot \mathcal I_N\mathcal I_N^{T} IN​INT​⋅IN​INT​=N⋅IN​INT​ 将该结果带入上式： H 2 = E N − 2 N I N I N T + 1 N I N I N T = E N − 1 N I N I N T = H \begin{aligned} \mathcal H^2 & = \mathcal E_N - \frac{2}{N}\mathcal I_N\mathcal I_N^{T} + \frac{1}{N}\mathcal I_N\mathcal I_N^{T} \\ & = \mathcal E_N - \frac{1}{N} \mathcal I_N \mathcal I_N^{T} \\ & = \mathcal H \end{aligned} H2​=EN​−N2​IN​INT​+N1​IN​INT​=EN​−N1​IN​INT​=H​

综上，因而有： H 2 = H ⋅ H = H T ⋅ H = H ⋅ H T = H \mathcal H^2 = \mathcal H \cdot \mathcal H = \mathcal H^{T} \cdot \mathcal H = \mathcal H \cdot \mathcal H^{T} = \mathcal H H2=H⋅H=HT⋅H=H⋅HT=H

回顾样本方差的矩阵表示，可以继续化简为如下形式： S = 1 N X T H ⋅ H T X = 1 N X T H ⋅ X \begin{aligned} \mathcal S & = \frac{1}{N} \mathcal X^{T} \mathcal H \cdot \mathcal H^{T}\mathcal X \\ & = \frac{1}{N} \mathcal X^{T} \mathcal H \cdot \mathcal X \end{aligned} S​=N1​XTH⋅HTX=N1​XTH⋅X​

至此，我们介绍了样本均值与样本方差的矩阵表达，以及中心矩阵的相关性质。下一节将介绍PCA降维。

相关参考： 机器学习-降维2-样本均值&样本方差的矩阵表示