机器学习笔记之降维(一)维数灾难

引言

本节将介绍降维算法，并介绍降维算法的相关背景。

回顾：过拟合

我们在正则化介绍与岭回归一节中介绍了正则化的基本思想，正则化操作通过约束模型参数 W \mathcal W W的取值来处理过拟合现象。在线性回归任务中，基于岭回归的最小二乘估计公式表示如下： L ( W ) = ∑ i = 1 N ∣ ∣ W T x ( i ) − y ( i ) ∣ ∣ 2 + λ ∣ ∣ W ∣ ∣ 2 2 \mathcal L(\mathcal W) = \sum_{i=1}^{N} ||\mathcal W^{T}x^{(i)} - y^{(i)}||^2 + \lambda ||\mathcal W||_2^2 L(W)=i=1∑N​∣∣WTx(i)−y(i)∣∣2+λ∣∣W∣∣22​ 从本节开始，将介绍从降维角度去处理过拟合问题。

维度灾难 从数值角度观察维数灾难

如果我们使用线性回归或者线性分类 处理相关任务时，样本自身维度过高会给机器学习过程带来什么样的影响？

收到最直接影响的是维度灾难(Curse of Dimensionality)：在涉及向量计算的问题时，随着维数的增加，计算量呈指数倍增长的现象。

• 这种现象在样本数据充足的情况下，通常表现为机器学习过程中，由于计算机的算力和内存有限，从而需要更长的时间去执行任务。

• 其次，在样本有限的情况下，较高的样本维度可能导致 样本空间内的样本分布过于稀疏。实际上，每增加一个维度，需要增加指数倍的样本数量来维持样本分布不稀疏 的状态。

• 相反，如果针对稀疏样本执行机器学习任务，最终可能导致过拟合的产生。

为什么每增加一个维度，就需要增加指数倍的样本数量？举一个简单例子：

假设存在一组样本数据，该数据共包含2个特征，并且每个特征均服从伯努利分布，此时的样本可能存在如下几种情况：

样本编号特征1特征2100201310411

此时，我们至少需要4个样本才能描述完整特征空间。此时，若增加一个维度，增加的维度同样满足伯努利分布，那么我们 需要多少样本才能完整描述特征空间？ 自然是： 2 3 = 8 2^3 = 8 23=8个样本：

样本编号特征特征2特征310002001301040115100610171108111

此时，相比于2个特征的样本空间，3个特征的样本空间需要比之前多整整一倍的样本，才能完整描述特征空间。

同理，如果再次增加特征空间的维度，我们不得不再次使用 至少比上一次多一倍的样本数量来描述样本空间。但实际情况，样本特征可能是离散，也可能是连续，特征空间的复杂程度更加复杂，因而 需要的样本数量只多不少。

从几何角度观察维度灾难 示例1

在2维特征空间中存在一个特殊的特征空间，该特征空间的形状是边长为1的正方形，在该特征空间中包含两类样本：

• 在正方形中内嵌一个直径为1的圆，第一类样本在圆围成区域的内部；
• 而第二类样本在圆围成区域的外部；

具体描述如下图所示：

• 假设样本在该正方形区域中均匀分布，从该特征空间中进行采样，采样结果属于红色区域的概率 表示如下： P r e d = S c i r c u l a r S s q u a r e = π × ( 0.5 ) 2 1 2 = π 4 \mathcal P_{red} = \frac{\mathcal S_{circular}}{\mathcal S_{square}} = \frac{\pi \times (0.5)^2}{1^2} = \frac{\pi}{4} Pred​=Ssquare​Scircular​​=12π×(0.5)2​=4π​ 同理，采样结果属于橙色区域的概率 表示如下： P o r a n g e = S s q u a r e − S c i r c u l a r S s q u a r e = 1 − π 4 \mathcal P_{orange} = \frac{\mathcal S_{square} - \mathcal S_{circular}}{\mathcal S_{square}} = 1 - \frac{\pi}{4} Porange​=Ssquare​Ssquare​−Scircular​​=1−4π​

• 如果样本数量依然是均匀分布，但是将维度增加一维——意味着特征空间由正方形变成了正方体，圆也变成了球，此时我们再次对增加一维后的特征空间进行采样，采样结果属于 红色区域的概率 表示如下： P r e d ′ = V s p h e r o m e V c u b e = 4 3 × π ( 0.5 ) 3 1 3 = π 6 \mathcal P'_{red} = \frac{\mathcal V_{spherome}}{\mathcal V_{cube}} =\frac{\frac{4}{3} \times \pi(0.5)^3}{1^3} = \frac{\pi}{6} Pred′​=Vcube​Vspherome​​=1334​×π(0.5)3​=6π​

  发现一个问题：红色区域的部分随着维度的增加，它的比重越来越小 ( π 4 → π 6 ) \left(\frac{\pi}{4} \to \frac{\pi}{6}\right) (4π​→6π​)。如果继续增加维度，增加至维度 k k k，此时特征空间可理解为一个超立方体(Hypercube)，而红色区域可理解为一个超球体(hypersphere)，此时继续对该特征空间进行采样，采样结果属于 红色区域的概率 表示如下： P r e d ( k ) = V h y p e r s p h e r e V H y p e r c u b e = M × π ( 0.5 ) k 1 k \mathcal P^{(k)}_{red} = \frac{\mathcal V_{hypersphere}}{\mathcal V_{Hypercube}} = \frac{\mathcal M \times \pi (0.5)^k}{1^k} Pred(k)​=VHypercube​Vhypersphere​​=1kM×π(0.5)k​ 其中， M \mathcal M M表示常数，当维度 k k k趋于无穷大时， P r e d ( k ) \mathcal P^{(k)}_{red} Pred(k)​趋近于0： l i m k → ∞ M × π ( 0.5 ) k = 0 \mathop{lim}\limits_{k \to \infty} \mathcal M \times \pi(0.5)^k = 0 k→∞lim​M×π(0.5)k=0 换句话说，在维度足够大的条件下，我们是 极难采样到红色区域的样本。

• 继续假设，如果只增加特征空间的维度，而对应的样本数量不发生变化，此时随着维度的增高，红色区域中最终不存在任何样本(从中采集样本的概率是0)，所有样本均位于橙色区域部分。 此时造成了数据的‘稀疏性’。

  此时，特征空间的样本分布呈现一种中空状态，样本分布极不均匀。 随着维度的增加，红色区域(超球体的体积)在坍缩，而特征空间的数值(超立方体的体积不发生任何变化) 红色区域具体是如何坍缩的？仍然以2维提升到3维为例，如果2维提升到3维想要保证概率结果不变，可以想象成立方体内部嵌入一个‘圆柱’，而圆柱体积与球体积的差值就是红色区域坍缩的部分。

示例2

在2维特征空间中存在一个特殊的特征空间，该特征空间的形状是 半径为1的圆围成的空间。 此时存在一个区域，形状也为圆形，与特征空间共用同一个圆心，其半径为 1 − ϵ ( 1 > ϵ > 0 ) 1 - \epsilon(1> \epsilon > 0) 1−ϵ(1>ϵ>0)。具体图像表示如下： ε是一个极小的正值。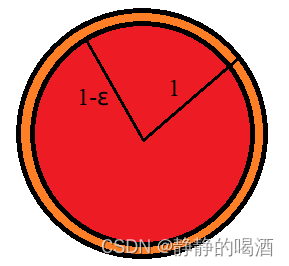

• 同示例1，假设样本在特征空间中均匀分布，从该特征空间中进行采样，采样到红色区域样本的概率表示如下： P r e d = π × ( 1 − ϵ ) 2 π × 1 2 = ( 1 − ϵ ) 2 \mathcal P_{red} = \frac{\pi \times (1 - \epsilon)^2}{\pi \times 1^2} = (1 - \epsilon)^2 Pred​=π×12π×(1−ϵ)2​=(1−ϵ)2 此时，如果 ϵ \epsilon ϵ较小时，如 ϵ = 0.01 \epsilon = 0.01 ϵ=0.01，此时选中红色区域样本的概率是较高的： P r e d = ( 1 − 0.01 ) 2 = 0.9801 \mathcal P_{red} = (1 - 0.01)^2 = 0.9801 Pred​=(1−0.01)2=0.9801
• 如果将特征空间的维度由二维增加到三维，固定 ϵ = 0.01 \epsilon=0.01 ϵ=0.01，继续对特征空间进行采样，采样到红色区域样本的概率表示如下： P r e d ′ = 4 3 π × ( 1 − ϵ ) 3 4 3 π × 1 3 = ( 1 − ϵ ) 3 \mathcal P'_{red} = \frac{\frac{4}{3} \pi \times (1 - \epsilon)^3}{\frac{4}{3} \pi \times 1^3} = (1 - \epsilon)^3 Pred′​=34​π×1334​π×(1−ϵ)3​=(1−ϵ)3 ϵ = 0.01 \epsilon = 0.01 ϵ=0.01时，对应概率结果为： P r e d ′ = ( 1 − 0.01 ) 3 = 0.970299 \mathcal P'_{red} = (1 - 0.01)^3 = 0.970299 Pred′​=(1−0.01)3=0.970299 和示例1一样，随着维度的增加，红色区域的概率比重，坍缩了。 如果维度继续增加，增加到100维，500维，对应的概率结果表示为： P r e d ( 100 ) ≈ 0.3660 P r e d ( 500 ) ≈ 0.0066 \mathcal P^{(100)}_{red} \approx 0.3660\quad \mathcal P^{(500)}_{red} \approx 0.0066 Pred(100)​≈0.3660Pred(500)​≈0.0066 随着维度的增加，我们在红色区域采出样本的概率越来越小，最终概率无限趋近于0。此时的样本点全部分布于高维球空间的橙色区域，而红色区域的样本点分布几乎不存在，两者分布极不均匀。

相关参考： 维数灾难——百度百科 机器学习-降维1-背景介绍