机器学习笔记之降维(四)从最小重构代价角度观察主成分分析

引言

上一节介绍了主成分分析以及最大投影方差角度对表示主成分的特征方向进行求解，本节将从最小重构代价角度观察主成分分析，并从最小重构代价角度求解表示主成分的特征方向。

回顾：主成分分析与最大投影方差

主成分分析(Principle Component Analysis)的本质是对原始特征空间的重构，具体动机是针对原始特征空间中可能存在线性相关的特征，使用一系列正交变换将其转化为一组两两相互正交的正交基。

而最大投影方差的思想是：以原始样本点到某一特征方向的投影结果方差达到最大的特征方向作为第一个主成分，从而找到一组相互正交的正交基。

投影方差结果对应数学符号表达如下： J = u ⃗ T ⋅ [ 1 N ∑ i = 1 N ( x ( i ) − X ˉ ) ( x ( i ) − X ˉ ) T ] ⋅ u ⃗ = u ⃗ T ⋅ S ⋅ u ⃗ \begin{aligned} \mathcal J & = \vec u^{T} \cdot \left[\frac{1}{N} \sum_{i=1}^N \left(x^{(i)} - \bar {\mathcal X}\right)\left(x^{(i)} - \bar {\mathcal X}\right)^{T}\right] \cdot \vec u \\ & = \vec u^{T} \cdot \mathcal S \cdot \vec u \end{aligned} J​=u T⋅[N1​i=1∑N​(x(i)−Xˉ)(x(i)−Xˉ)T]⋅u =u T⋅S⋅u ​

其中， u ⃗ \vec u u 表示要求解的最优特征方向的正交基， S \mathcal S S表示中心化后样本点的协方差矩阵；通常设 ∣ u ⃗ ∣ = 1 |\vec u| = 1 ∣u ∣=1，即正交基 ∣ u ⃗ ∣ |\vec u| ∣u ∣是一组单位向量。

至此，最大投影方差思想对应的数学符号表示如下： { arg ⁡ max ⁡ u ⃗ J s . t . ∣ u ⃗ ∣ = 1 \begin{cases} \mathop{\arg\max}\limits_{\vec u} \mathcal J \\ s.t. \quad |\vec u| = 1 \end{cases} ⎩ ⎨ ⎧​u argmax​Js.t.∣u ∣=1​

通过拉格朗日乘数法对上述带约束条件的优化问题进行求解： L ( u ⃗ , λ ) = u ⃗ T ⋅ S ⋅ u ⃗ + λ ( 1 − u ⃗ T ⋅ u ⃗ ) ∂ L ( u ⃗ , λ ) ∂ u ⃗ ≜ 0 → S ⋅ u ⃗ = λ ⋅ u ⃗ \mathcal L(\vec u,\lambda) = \vec u^{T} \cdot \mathcal S \cdot \vec u + \lambda(1 - \vec u^{T} \cdot \vec u) \\ \frac{\partial \mathcal L(\vec u,\lambda)}{\partial \vec u} \triangleq 0 \to \mathcal S \cdot \vec u = \lambda \cdot \vec u L(u ,λ)=u T⋅S⋅u +λ(1−u T⋅u )∂u ∂L(u ,λ)​≜0→S⋅u =λ⋅u 至此，待求解的最优特征方向的正交基就是中心化后样本的协方差矩阵 S \mathcal S S对应特征值的特征向量。

最终，按照特征值的大小顺序分别求解出第一、第二、……第 p p p主成分。

从最小重构代价角度观察主成分分析 重构代价

在主成分分析的介绍中提到了 特征空间的重构，那么如何理解重构代价？ 以2维特征空间为例，已知某样本 x ( i ) = ( x 1 ( i ) , x 2 ( i ) ) T x^{(i)}=\left(x_1^{(i)},x_2^{(i)}\right)^{T} x(i)=(x1(i)​,x2(i)​)T在特征空间重构之后得到的新的向量结果 x ( i ) = ( u 1 ⃗ ( i ) , u 2 ⃗ ( i ) ) T x^{(i)} = \left(\vec{u_1}^{(i)},\vec{u_2}^{(i)}\right)^{T} x(i)=(u1​ ​(i),u2​ ​(i))T图像表示如下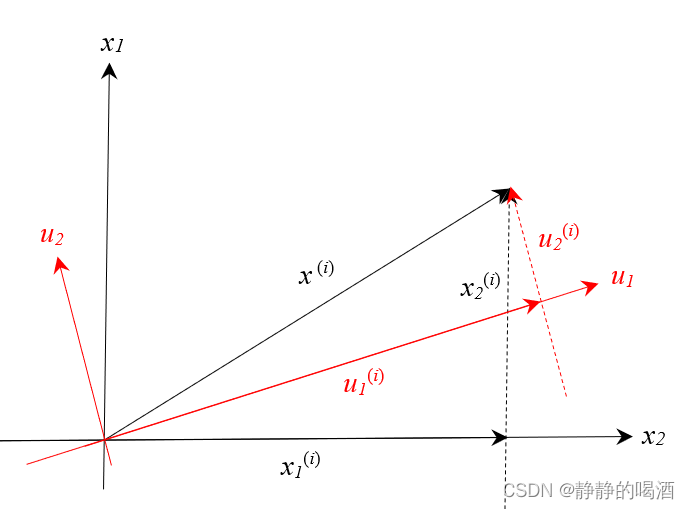： 根据向量的加法公式，样本点 x ( i ) x^{(i)} x(i)表示的向量基于 u 1 ⃗ , u 2 ⃗ \vec{u_1},\vec{u_2} u1​ ​,u2​ ​正交基表示如下： 该表示方法的推导过程详见上一节传送门 u 1 ⃗ ( i ) = [ x ( i ) ] T ⋅ u 1 ⃗ u 2 ⃗ ( i ) = [ x ( i ) ] T ⋅ u 2 ⃗ x ( i ) = [ ( x ( i ) ) T ⋅ u 1 ⃗ , ( x ( i ) ) T ⋅ u 2 ⃗ ] T = [ ( x ( i ) ) T ⋅ u 1 ⃗ ] ⋅ u 1 ⃗ + [ ( x ( i ) ) T ⋅ u 2 ⃗ ] ⋅ u 2 ⃗ \begin{aligned} \vec{u_1}^{(i)} & = \left[x^{(i)}\right]^{T}\cdot \vec{u_1} \\ \vec{u_2}^{(i)} & = \left[x^{(i)}\right]^{T}\cdot \vec{u_2} \\ x^{(i)} & = \left[\left(x^{(i)}\right)^{T}\cdot \vec{u_1},\left(x^{(i)}\right)^{T}\cdot \vec{u_2}\right]^{T} \\ & = \left[\left(x^{(i)}\right)^{T}\cdot \vec{u_1}\right] \cdot \vec{u_1} + \left[\left(x^{(i)}\right)^{T}\cdot \vec {u_2} \right] \cdot \vec{u_2} \end{aligned} u1​ ​(i)u2​ ​(i)x(i)​=[x(i)]T⋅u1​ ​=[x(i)]T⋅u2​ ​=[(x(i))T⋅u1​ ​,(x(i))T⋅u2​ ​]T=[(x(i))T⋅u1​ ​]⋅u1​ ​+[(x(i))T⋅u2​ ​]⋅u2​ ​​ 注意：写成上述格式的原因：

• [ ( x ( i ) ) T ⋅ u 1 ⃗ ] \left[\left(x^{(i)}\right)^{T}\cdot \vec{u_1}\right] [(x(i))T⋅u1​ ​]中 ( x ( i ) ) T \left(x^{(i)}\right)^{T} (x(i))T是 1 × p 1 \times p 1×p的向量，而 u 2 u_2 u2​是一个模为1的单位向量 p × 1 p \times 1 p×1，因而 [ ( x ( i ) ) T ⋅ u 1 ⃗ ] \left[\left(x^{(i)}\right)^{T}\cdot \vec{u_1}\right] [(x(i))T⋅u1​ ​]的结果是一个标量或者看成一个系数。对应的 [ ( x ( i ) ) T ⋅ u 1 ⃗ ] ⋅ u 1 ⃗ \left[\left(x^{(i)}\right)^{T}\cdot \vec{u_1}\right] \cdot \vec{u_1} [(x(i))T⋅u1​ ​]⋅u1​ ​可表示为如下二维向量： [ ( x ( i ) ) T ⋅ u 1 ⃗ ] ⋅ u 1 ⃗ = [ [ x ( i ) ] T ⋅ u 1 ⃗ 0 ] \left[\left(x^{(i)}\right)^{T}\cdot \vec{u_1}\right] \cdot \vec{u_1} = \begin{bmatrix}\left[x^{(i)}\right]^{T}\cdot \vec{u_1} \\ 0\end{bmatrix} [(x(i))T⋅u1​ ​]⋅u1​ ​=[[x(i)]T⋅u1​ ​0​]
• 同理， [ ( x ( i ) ) T ⋅ u 2 ⃗ ] ⋅ u 2 ⃗ \left[\left(x^{(i)}\right)^{T}\cdot \vec{u_2}\right] \cdot \vec{u_2} [(x(i))T⋅u2​ ​]⋅u2​ ​也可表示为如下二维向量格式： [ ( x ( i ) ) T ⋅ u 2 ⃗ ] ⋅ u 2 ⃗ = [ 0 [ x ( i ) ] T ⋅ u 2 ⃗ ] \left[\left(x^{(i)}\right)^{T}\cdot \vec{u_2}\right] \cdot \vec{u_2} = \begin{bmatrix}0 \\\left[x^{(i)}\right]^{T}\cdot \vec{u_2}\end{bmatrix} [(x(i))T⋅u2​ ​]⋅u2​ ​=[0[x(i)]T⋅u2​ ​​]
• 因而两向量相加结果为： [ [ x ( i ) ] T ⋅ u 1 ⃗ 0 ] + [ 0 [ x ( i ) ] T ⋅ u 2 ⃗ ] = [ [ x ( i ) ] T ⋅ u 1 ⃗ [ x ( i ) ] T ⋅ u 2 ⃗ ] = x ( i ) \begin{bmatrix}\left[x^{(i)}\right]^{T}\cdot \vec{u_1} \\ 0\end{bmatrix} + \begin{bmatrix}0 \\\left[x^{(i)}\right]^{T}\cdot \vec{u_2}\end{bmatrix} = \begin{bmatrix}\left[x^{(i)}\right]^{T}\cdot \vec{u_1} \\ \left[x^{(i)}\right]^{T}\cdot \vec{u_2}\end{bmatrix} = x^{(i)} [[x(i)]T⋅u1​ ​0​]+[0[x(i)]T⋅u2​ ​​]=[[x(i)]T⋅u1​ ​[x(i)]T⋅u2​ ​​]=x(i)

同理，将上述二维特征空间延伸至高维特征空间，假设基于原始样本 x ( i ) ∈ X x^{(i)} \in \mathcal X x(i)∈X的 p p p维特征表示如下： x ( i ) = ( x 1 ( i ) , x 2 ( i ) , ⋯   , x p ( i ) ) T x^{(i)} = \left(x_1^{(i)},x_2^{(i)},\cdots,x_p^{(i)}\right)^{T} x(i)=(x1(i)​,x2(i)​,⋯,xp(i)​)T 我们通过特征空间重构(如最大投影方差)的方式得到了这样一组正交基。正交基内部的特征向量与对应的特征值结果 表示如下：

特征值 λ 1 \lambda_1 λ1​ λ 2 \lambda_2 λ2​ ⋯ \cdots ⋯ λ p \lambda_p λp​特征向量 u 1 ⃗ \vec {u_1} u1​ ​ u 2 ⃗ \vec {u_2} u2​ ​ ⋯ \cdots ⋯ u p ⃗ \vec {u_p} up​ ​

如果特征重构过程中没有丢失信息，那么特征空间重构条件下样本点 x ( i ) x^{(i)} x(i)结果表达如下： x ( i ) = [ ( x ( i ) ) T ⋅ u 1 ⃗ ] ⋅ u 1 ⃗ + [ ( x ( i ) ) T ⋅ u 2 ⃗ ] ⋅ u 2 ⃗ + ⋯ + [ ( x ( i ) ) T ⋅ u p ⃗ ] ⋅ u p ⃗ = ∑ k = 1 p [ ( x ( i ) ) T ⋅ u k ⃗ ] ⋅ u k ⃗ \begin{aligned} x^{(i)} & = \left[\left(x^{(i)}\right)^{T} \cdot \vec{u_1}\right] \cdot \vec{u_1} + \left[\left(x^{(i)}\right)^{T} \cdot \vec{u_2}\right] \cdot \vec{u_2} + \cdots + \left[\left(x^{(i)}\right)^{T} \cdot \vec{u_p}\right] \cdot \vec{u_p} \\ & = \sum_{k=1}^{p} \left[\left(x^{(i)}\right)^{T} \cdot \vec{u_k}\right] \cdot \vec{u_k} \end{aligned} x(i)​=[(x(i))T⋅u1​ ​]⋅u1​ ​+[(x(i))T⋅u2​ ​]⋅u2​ ​+⋯+[(x(i))T⋅up​ ​]⋅up​ ​=k=1∑p​[(x(i))T⋅uk​ ​]⋅uk​ ​​

但执行特征重构的核心出发点是降维，我们希望以较小的信息损失为代价，降低特征空间的维度，使其避免出现维数灾难的现象。

因此，基于上述特征重构结果，选择 最大的 q q q个特征值对应的特征向量，其余特征值结果忽略不计。

这种操作极大概率导致样本点的特征信息造成损失，为区别于 x ( i ) x^{(i)} x(i)，执行降维操作后 的样本点 x ^ ( i ) \hat {x}^{(i)} x^(i)结果表达如下： x ^ ( i ) = ∑ k = 1 q [ ( x ( i ) ) T ⋅ u k ⃗ ] ⋅ u k ⃗ \hat x^{(i)} = \sum_{k=1}^q \left[\left(x^{(i)}\right)^{T} \cdot \vec{u_k}\right] \cdot \vec{u_k} x^(i)=k=1∑q​[(x(i))T⋅uk​ ​]⋅uk​ ​

那么重构代价表示样本点重构前与重构后之间差值的模： ∣ x ( i ) − x ^ ( i ) ∣ = ∣ ∣ x ( i ) − x ^ ( i ) ∣ ∣ 2 |x^{(i)} - \hat {x}^{(i)}| = \sqrt{||x^{(i)} - \hat {x}^{(i)}||^2} ∣x(i)−x^(i)∣=∣∣x(i)−x^(i)∣∣2 ​ 由于根号操作在 ∣ ∣ x ( i ) − x ^ ( i ) ∣ ∣ 2 ||x^{(i)} - \hat {x}^{(i)}||^2 ∣∣x(i)−x^(i)∣∣2的值域中单调递增，因而不影响最值的取值结果。因此为了方便运算，去掉根号。那么样本点 x ( i ) x^{(i)} x(i)的重构代价表示如下： ∣ ∣ x ( i ) − x ^ ( i ) ∣ ∣ 2 ||x^{(i)} - \hat {x}^{(i)}||^2 ∣∣x(i)−x^(i)∣∣2 因此，数据集合 X \mathcal X X中的 N N N个样本点的重构总代价表示如下： ∑ i = 1 N ∣ ∣ x ( i ) − x ^ ( i ) ∣ ∣ 2 \sum_{i=1}^{N} ||x^{(i)} - \hat x^{(i)}||^2 i=1∑N​∣∣x(i)−x^(i)∣∣2 为了方便运算，我们添加一个系数 1 N \frac{1}{N} N1​，最终样本集合的重构代价结果 J \mathcal J J表示如下： 与上面的根号相似，常数 1 N \frac{1}{N} N1​并不影响最值的取值结果。 J = 1 N ∑ i = 1 N ∣ ∣ x ( i ) − x ^ ( i ) ∣ ∣ 2 \mathcal J = \frac{1}{N} \sum_{i=1}^N ||x^{(i)} - \hat {x}^{(i)}||^2 J=N1​i=1∑N​∣∣x(i)−x^(i)∣∣2

重构代价的整理过程

我们将 x ( i ) x^{(i)} x(i)和 x ^ ( i ) \hat x^{(i)} x^(i)分别代入： 基于降维的条件下， q < p q < p q