29.CF1149C [Tree Generator™](httpswww.luogu.com.cnproblemCF1149C) 区间合并线段树

29.CF1149C Tree Generator™ 区间合并线段树

个人Limitの线段树题单题解主目录：Limitの线段树题单 题解目录_HeartFireY的博客-CSDN博客

给定一棵树的括号序列，要求支持单点修改、查询树直径

考虑区间合并线段树，每个子树的括号序列是按照先序遍历进行的，因此考虑合并两个区间的括号序列时的情况 若从序列中任取一段连续子序列，从中去掉所有匹配括号后，剩下的括号组成的路径一定为一条链，链长为剩下的子序列 树上直径长度即为任意区间去掉匹配括号后的长度的最大值。 最长去匹配区间 = 最大的（将区间分成两段）后面的权值和 - 前面的权值和

洛谷传送门：Tree Generator™

CF传送门：C. Tree Generator™ (codeforces.com)

题目分析

给定一棵树的括号序列，要求支持单点修改、查询树直径。

区间合并线段树，只是要合并的信息有点多。

如上图所示，是一颗树，其直径由红线构成，其括号序列为 ( ( ) ( ) ) ( ( ) ( ) ) (()())(()()) (()())(()())。可以发现 ( ( (即为递归搜索 ) ) )为回溯。我们可以发现：

若从序列中任取一段连续子序列，从中去掉所有匹配括号后，剩下的括号组成的路径一定为一条链，链长为剩下的子序列长。

那么不难想到树上两点间最长的简单路径就是所有区间中去匹配括号长度的最大值，例如上面就可以是 ) ) ( ( ))(( ))((。长度为 4 4 4 。

我们不难发现，由于已经匹配的括号带有回溯步骤，对最终答案没有贡献。因此最终直径的序列一定是下列三种之一：

• … ( ( ( ( ( ( … \dots (((((( \dots …((((((…
• …   ) ) ) ) ) ) … \dots )))))) \dots …))))))…
• …   ) ) ) ( ( ( … \dots )))((( \dots …)))(((…

不难发现，前两种都是第三种的极端情况，我们设反转的位置叫序列中点，那么第一种中点在头部，第二种中点在尾部。

那么按照括号序列的经典处理套路，我们令 ′ ( ′ = 1 '(' = 1 ′(′=1, ′ ) ′ = − 1 ')' = -1 ′)′=−1，那么我们可以得到最长去匹配区间的计算方法：我们可以将这种序列表达为连续左括号(一堆1) − - −连续右括号(一堆-1)，也就是最大的后半段权值和-前半段权值和。

那么我们考虑如何维护这个东西，发现类似区间最大子段和，很有区间合并线段树的感觉。那么就考虑如何用区间合并线段树解决。

我们首先需要维护区间和：

res.val = a.val + b.val;

接下来可以维护最大子段和，也就是左右连续选取最大值、无限制连续选取最大值，这个是很经典的套路：

分别讨论跨区间取值即可：

res.lmax = max(a.lmax, b.lmax + a.val), res.lmin = min(a.lmin, b.lmin + a.val);
res.rmax = max(b.lmax, a.rmax + b.val), res.rmin = min(b.rmin, a.rmin + b.val);

维护完了最大子段和，我们需要维护左右起连续选取最大的权值和(去匹配权值和)差值：

考虑序列中点(见前文描述)跨区间问题，以下为左起选取序列的情况，我们分别枚举序列中点在左右时的情况

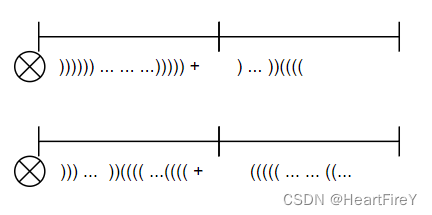
右起的选取与左侧类似，那么我们可以得到合并左右区间的序列选取

res.lcmax = max({a.lcmax, b.lcmax - a.val, a.amax + b.lmax});
res.rcmax = max({b.rcmax, a.rcmax + b.val, b.amax - a.rmin});

接下来就可以维护选取整个区间下的去匹配最大值，这与上面的选取方式是相同的：

res.amax = max(a.amax + b.val, b.amax - a.val);

有了上面的值，我们就可以计算合并后的无限制去匹配最大差值，这仍采用枚举中心点的方式合并计算：

res.ans = max({a.ans, b.ans, b.lcmax - a.rmin, a.rcmax + b.lmax});

至此，区间合并得到了最终答案。

确实是一道非常好的区间合并练习题！

Code

#include 
#define int long long 
#define endl '\n'
using namespace std;

const int N = 2e5 + 10;

string str;

namespace SegTree{
    #define ls rt  n >> m, n = (n - 1)  str, str = '@' + str;
    SegTree::build(SEGRG);
    cout  r;
        if(str[l] != str[r]){
            swap(str[l], str[r]);
            SegTree::update(SEGRG, l);
            SegTree::update(SEGRG, r);
        }
        cout