##点斜式求直线交点: m0 = (y1 - y0) / (x1 - x0);
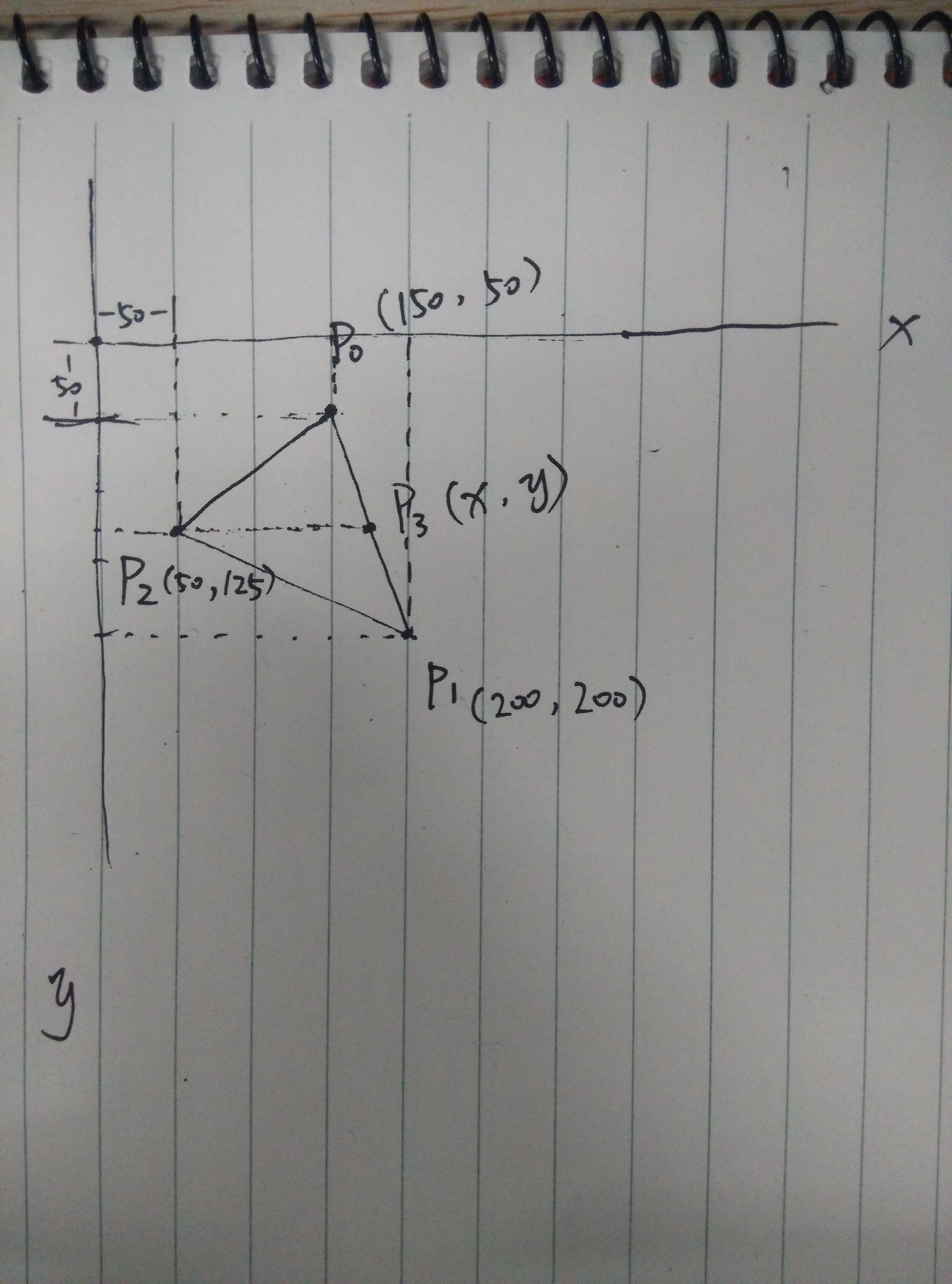
####已知: P0=(X:150, Y:50); P1=(X:200, Y:200); P2=(X:50, Y:125); P3=(X:?, Y:?);
####直线: L1 = P0-P1; L2 = P2-P3;
P3点是:从P2作平行于X轴的直线L2,直到与L1相交的点;
两线相交于:P3 因此L1可以写成:L1 = P0-P3;
求P3的坐标:#
m1 = (P0.Y-P1.Y) / (P0.X-P1.X); m1 = (50-200) / (150-200) = 150 / 50 = 3; m1 = 3;
m2 = 0;因平行于X轴;
再列出L1,L2的点斜率式: L1的斜率:m1 = (P0.Y-P1.Y) / (P0.X-P1.X); 之前这里写错,P3写成P1,(P0.Y-P3.Y) / (P0.X-P3.X),感谢 问道江湖 网友指正 L2的斜率:m2 = (P2.Y-P3.Y) / (P2.X-P3.X);
由于:m1 = 3, m2 = 0; 代入m1, m3后,再代入P0, P2三点对应的X,Y值后,L1, L2分别为: L1: 3 = (50 - Y) / (150 - X);
L2: 0 = (125 - Y) / (50 - X);
L2代简,可得Y或X,我们选Y先: 先:两边乘以(50 - X) 0 * (50 - X) = (125 - Y) / (50 - X) * (50 - X); 0 = (125 - Y); 两点再-125; 0 - 125; = 125 - Y - 125; -125 = -Y; 125 = Y; 最终得: Y = 125;
再Y代入L1中 3 = (50 - 125) / (150 - X); 可求出X 先:两边乘以(150 - X),(我们把过程加速,不用写得太详细) 3 * (150 - X) = 50 - 125; 450 - 3X = -75; -3X = -75 - 450; X = (75 + 450) / 3; X = 525 / 3; X = 175;
最终得: P3的X,Y为分别是: X = 175; Y = 125;
另外附加信息 斜截式,求交点: Y = K * X + B; K = 斜率; B = 截距; 在已知:的两条线的K,B,就可以求出对应交点的X,Y;
其它的两点式、一般式,等基本是一样的,只是推导转换后的关系;(实质是不同已知条件的处理方式)



