- Gouraud
- dot - 点积的作用
- 图形了解顶点点积的作用
- 漫反射
- 纯漫反射效果
- Diffuse - Shader
- GLSL 的中奇怪的问题
- 高光
- reflect - 反射高光方向
- GLSL 中的公式的不同
- view - 观察方向
- 纯高光效果
- Specular - Shader
- 实践
- Normal - 法线
- 关于法线从对象空间转换到世界空间
- diffuse effect - 漫反射效果
- Shader - 着色器
- Shader 中的 uniform
- 网格模型
- Assimp Lib
- .obj file format - .obj 文件格式
- References
前一篇:LearnGL - 11 - 光与颜色前置篇 了解了光与颜色的基本概念。
这篇:我们将对 Gouraud 光照模型实现一个简单的实现
因为一年前在 Unity 写过 Gouraud 与 Phong 的文章,时隔一年我又忘记了他们的叫法,之前把它们又搞混了名字,QAQ,所以下面有些图片显示:Phong 描述
本人才疏学浅,如有什么错误,望不吝指出。
GouraudGouraud Shading,也叫:高洛德着色模型,该光照模型是很简单的光照模型,只有:环境光、漫反射、高光。
- 环境光 用于模拟物体反射周围的物体颜色,在 Gouraud 中,只是纯颜色值作为环境光直接叠加。
- 漫反射 用于模拟光入射到物体后的各种散射后,最后又从物体射出的光,在 Gouraud 中,使用的是 lambert(兰伯特,或是half lambert半兰伯特) 漫反射模型,计算的是灯光方向与物体表面法线方向的夹角的余弦值。
- 高光 用于模拟物体对射入光按物体表现法线方向做反射出去的光,一般有 Gouraud 高光与 Blinn-Phong 高光模型。
计算公式,光照模型 I = i l l u m i n a t i o n I=illumination I=illumination: I = I a ⋅ K a + ∑ i = 0 n ( I d ⋅ K d ⋅ d o t ( N , L i ) + I s ⋅ K s ⋅ p o w ( d o t ( r e f l e c t ( − L i , N ) , V ) , G l o s s y ) ) I=I_a\cdot K_a+\sum_{i=0}^n(I_d\cdot K_d\cdot dot(N,L_i) + I_s\cdot K_s\cdot pow(dot(reflect(-L_i,N),V),Glossy)) I=Ia⋅Ka+∑i=0n(Id⋅Kd⋅dot(N,Li)+Is⋅Ks⋅pow(dot(reflect(−Li,N),V),Glossy))
其中:
- I a I_a Ia 是环境光,Gouraud 中这里就一个颜色值, K a K_a Ka 是环境光强度系数
- I d I_d Id 是漫反射颜色值, K d K_d Kd 是漫反射强度系数, d o t ( N , L ) dot(N,L) dot(N,L)是lambert 漫反射模型,其中 N N N是物体表面法线单温方向, L i L_i Li 是物体表面指向第 i i i个灯光的一个方向,也叫灯光方向,也是个单位向量。
- I s I_s Is 是高光颜色, K s K_s Ks 是高光强度系数, − L i -L_i −Li 是灯光方向的反方向,即:灯光入射方向, r e f l e c t ( − L i , N ) reflect(-L_i,N) reflect(−Li,N)求的是入射方向在根据法线方向反弹的高光反射反向,再用该用 V V V视角方向(从顶点到相机/镜头/观察者的方向),再用反射向量于 V V V视角方向求点积值,最后 G l o s s y Glossy Glossy是控制点积值的幂次。
上面的公式中,一般有些 Gouraud 光照是有限制 K d + K s = 1 K_d + K_s = 1 Kd+Ks=1,但我也看到过很多例子都不使用这个限制,我们可以在外部控制是否要有这个系数限制:只要 K d K_d Kd 和 K s K_s Ks 都是1的分量系数即可。
这里头值得说明一下的是, d o t dot dot的作用,在以前刚接触 shader 时,我根本不懂这个函数的作用,通过自己试验与网上资料查询后,才有所了解。
dot - 点积的作用在图形学中, d o t dot dot 的作用一定要了解,这里为了完善 LearnGL 系列笔记,我将以前学习理解的 d o t dot dot 特性、本质才简单的描述一下。
百度百科:点积
这里面我不想太多抄袭其他的专业的公式来表达,我只想表达我在图形学中什么情况下我会去用 d o t dot dot,这样才能更好理解它的作用。如果你喜欢看公式,你可以点击上面的链接,如果还是不满足你的求知欲,就 google 或是 wiki 中了解。
图形了解顶点点积的作用
如上图,有两个单位向量 u → \overrightarrow u u 和 v → \overrightarrow v v ,它们之前的夹角为 4 5 o 45^o 45o,然后 : d o t ( u , v ) = u ⋅ v = cos ( a ) = U d o t V = 0.71 dot(u,v)=u\cdot v=\cos(a)=UdotV=0.71 dot(u,v)=u⋅v=cos(a)=UdotV=0.71
为何也等于 cos ( a ) \cos(a) cos(a) 呢?
我们可以在上面说的百度百科中的公司: u → ⋅ v → = ∣ u → ∣ ⋅ ∣ v → ∣ ⋅ cos ( a ) \overrightarrow u\cdot \overrightarrow v=|\overrightarrow u|\cdot |\overrightarrow v|\cdot \cos(a) u ⋅v =∣u ∣⋅∣v ∣⋅cos(a)
如果我们两个都是单位向量 u → \overrightarrow u u 和 v → \overrightarrow v v ,它意味着向量长度为 1,即: ∣ u → ∣ = 1 , ∣ v → ∣ = 1 |\overrightarrow u| =1, |\overrightarrow v| =1 ∣u ∣=1,∣v ∣=1
那么上面的公式就变成: u → ⋅ v → = ∣ u → ∣ ⋅ ∣ v → ∣ ⋅ cos ( a ) ⟶ u → ⋅ v → = 1 ⋅ 1 ⋅ cos ( a ) ⟶ u → ⋅ v → = cos ( a ) \overrightarrow u\cdot \overrightarrow v=|\overrightarrow u|\cdot |\overrightarrow v|\cdot \cos(a) \longrightarrow \overrightarrow u\cdot \overrightarrow v=1 \cdot 1\cdot \cos(a) \longrightarrow \overrightarrow u\cdot \overrightarrow v=\cos(a) u ⋅v =∣u ∣⋅∣v ∣⋅cos(a)⟶u ⋅v =1⋅1⋅cos(a)⟶u ⋅v =cos(a)
而 cos ( a ) \cos(a) cos(a) 可以理解为初中学的 余 弦 函 数 = 邻 边 斜 边 余弦函数=\frac{邻边}{斜边} 余弦函数=斜边邻边
在下图就可以理解为是 c o s ( a ) = ∣ A D ∣ ∣ v → ∣ cos(a)=\frac{|AD|}{|\overrightarrow v|} cos(a)=∣v ∣∣AD∣, ∣ A D ∣ |AD| ∣AD∣ 就是邻边, ∣ v → ∣ |\overrightarrow v| ∣v ∣就是斜边,而 ∣ v → ∣ = 1 |\overrightarrow v|=1 ∣v ∣=1,所以 c o s ( a ) = ∣ A D ∣ 1 = ∣ A D ∣ cos(a)=\frac{|AD|}{1}=|AD| cos(a)=1∣AD∣=∣AD∣

这个值有什么用呢?
我们通过GIF动态图了解一下这个值的规律: 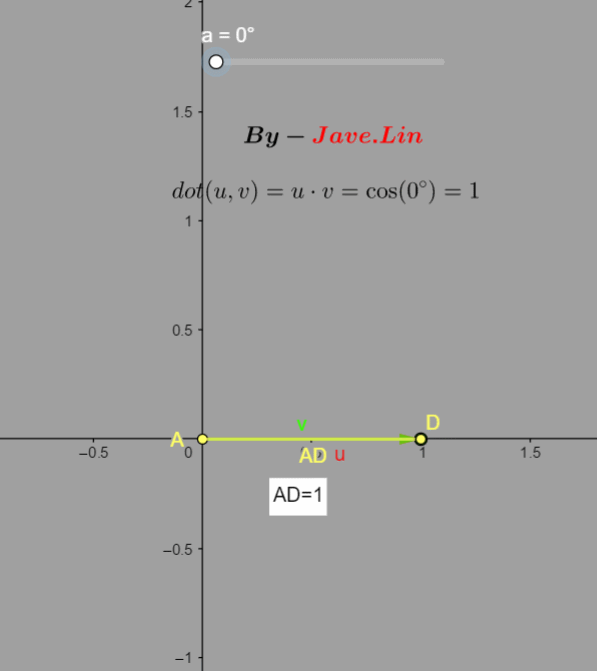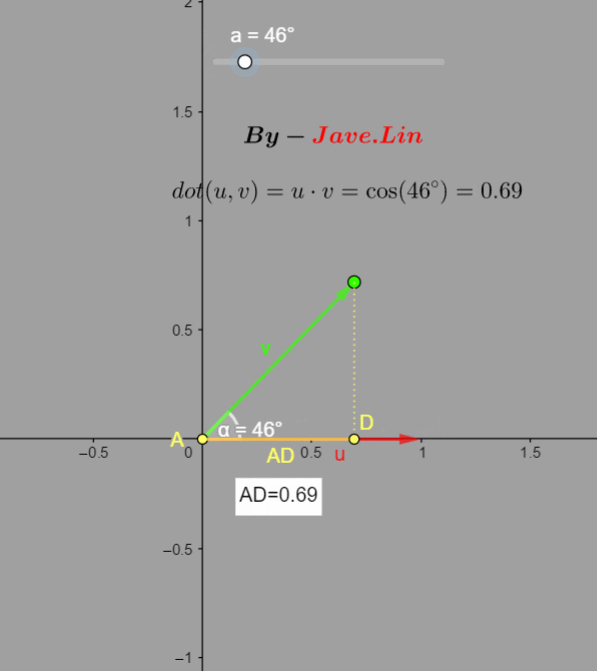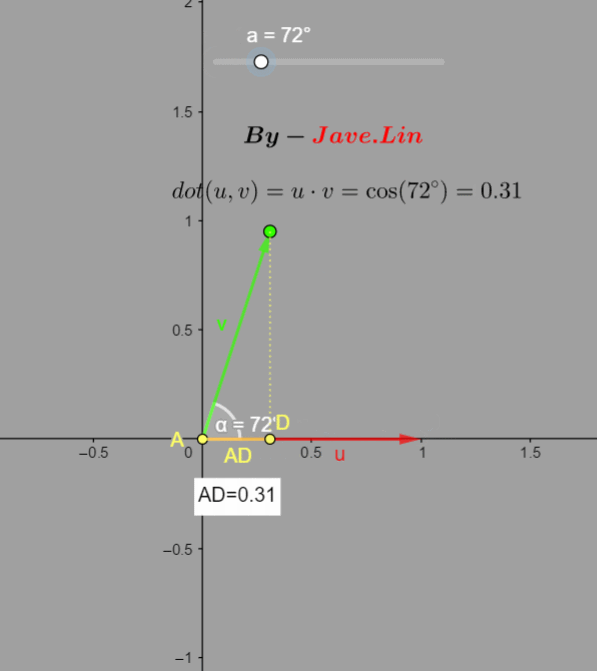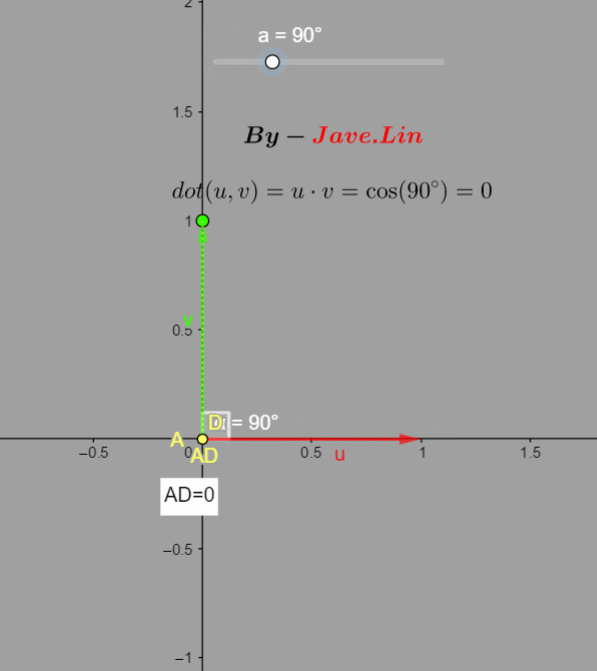 可以看到:
a
=
0
o
a=0^o
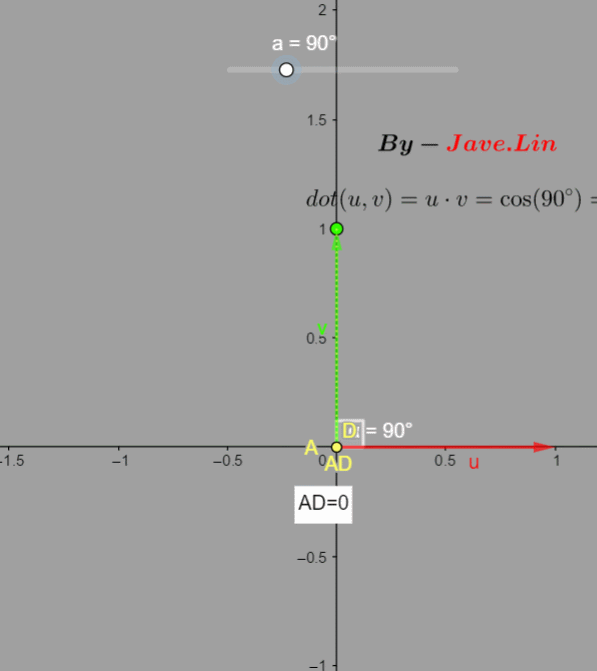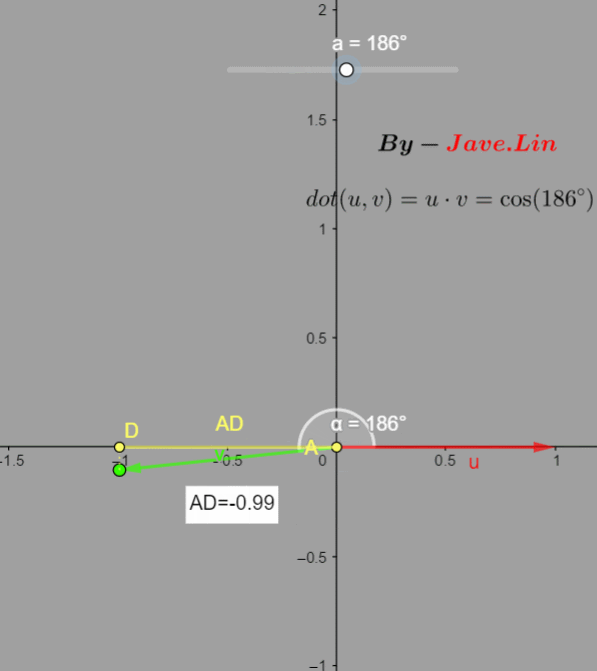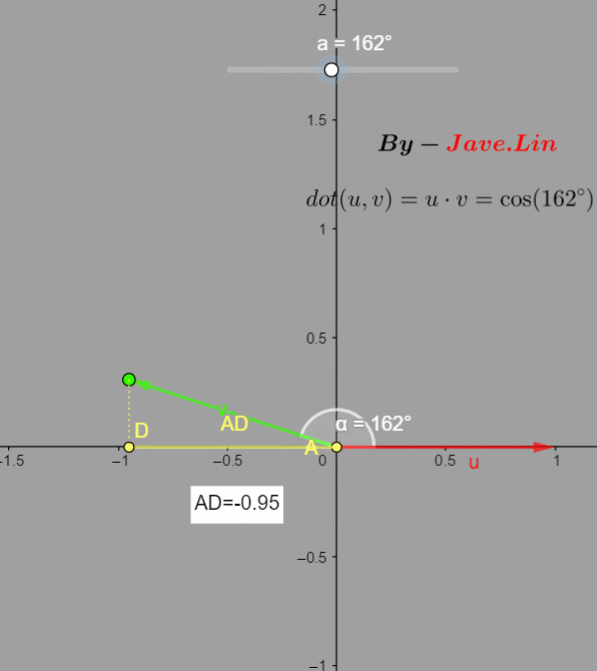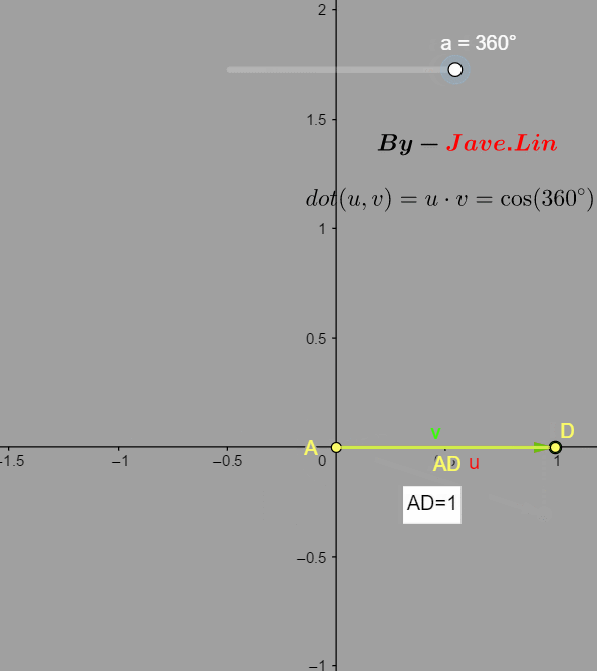
a=0o,点积值1,
a
=
9
0
p
a=90^p
a=90p,点积值0。
可以看到:
a
=
0
o
a=0^o
a=0o,点积值1,
a
=
9
0
p
a=90^p
a=90p,点积值0。
 a
=
18
0
o
a=180^o
a=180o,点积值-1。
a
=
18
0
o
a=180^o
a=180o,点积值-1。
通过这两点,可以总结: d o t dot dot可以用于判断两个向量的方向相似程度,越相似值越接近1,垂直为0,越反向值接近-1。
这在我们计算 漫反射 与 高光都会用到: I = I a ⋅ K a + ∑ i = 0 n ( I d ⋅ K d ⋅ d o t ( N , L i ) + I s ⋅ K s ⋅ p o w ( d o t ( r e f l e c t ( − L i , N ) , V ) , G l o s s y ) ) I=I_a\cdot K_a+\sum_{i=0}^n(I_d\cdot K_d\cdot \red{dot(N,L_i)} + I_s\cdot K_s\cdot pow(\red{dot(reflect(-L_i,N),V)},Glossy)) I=Ia⋅Ka+∑i=0n(Id⋅Kd⋅dot(N,Li)+Is⋅Ks⋅pow(dot(reflect(−Li,N),V),Glossy))
漫反射
d
o
t
(
N
,
L
i
)
\red{dot(N,L_i)}
dot(N,Li) 说明,
N
N
N 法线 与 第
i
i
i 个
L
i
L_i
Li 灯光方向 越相似,那么漫反射就越大 
如,上图,
N
N
N 是法线方向,
L
L
L 是灯光方向,如果这两个向量反向越是相似,那么交点
I
I
I 的漫反射值就越大。 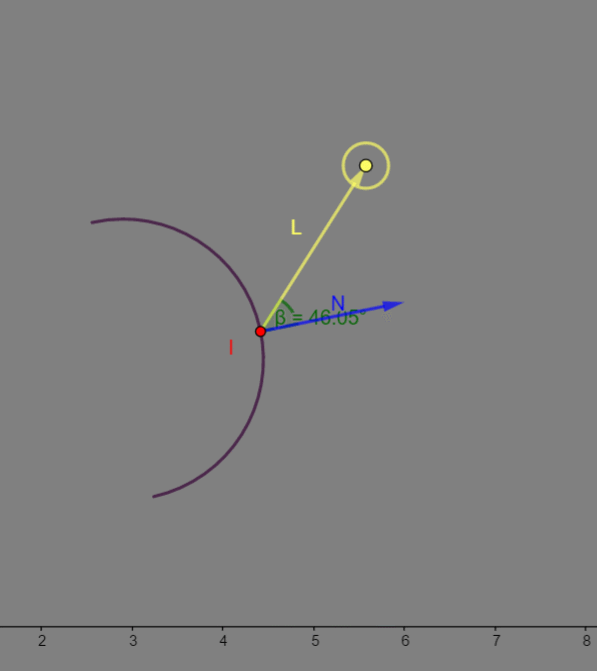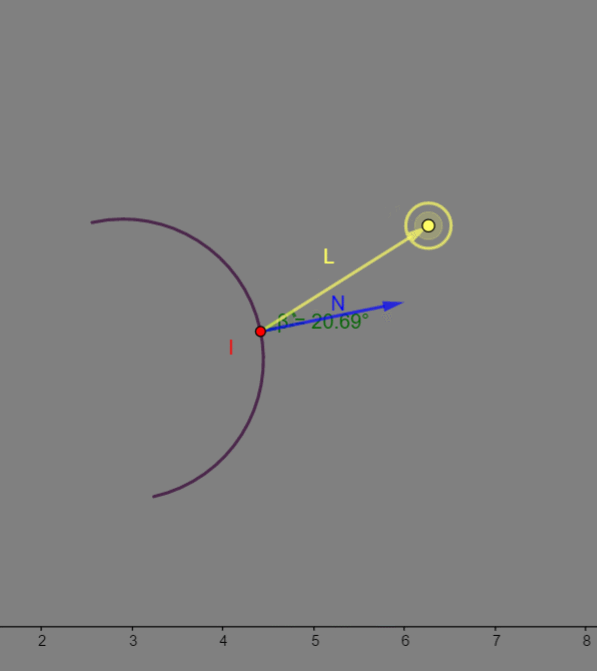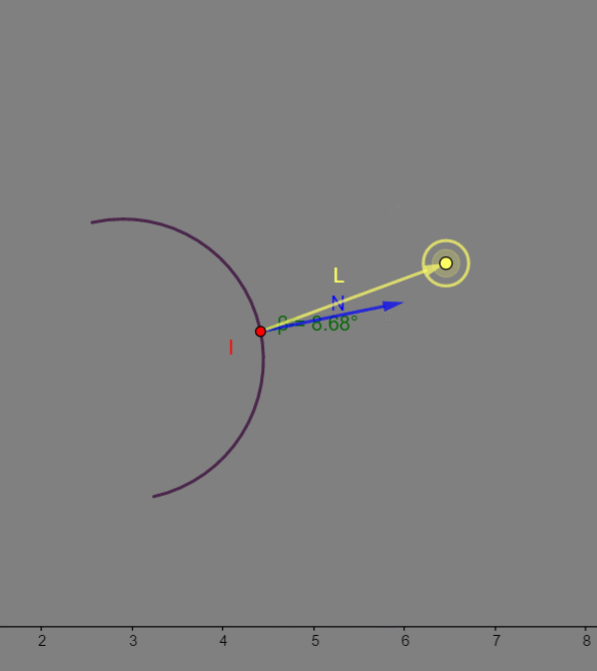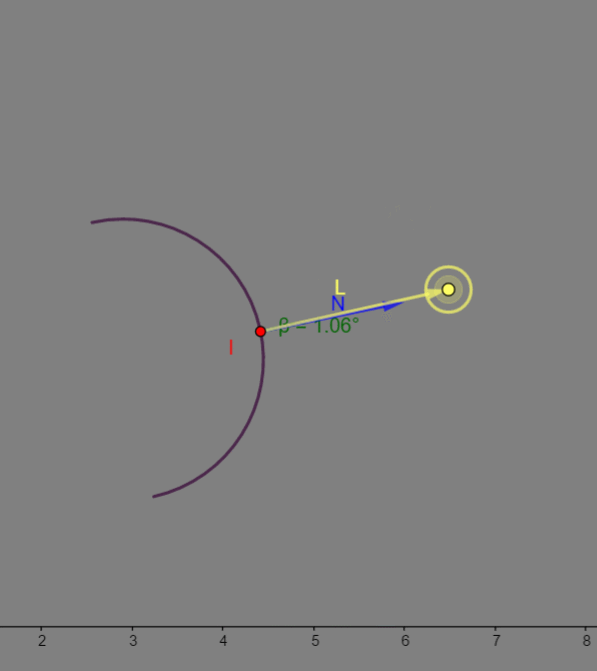 如上图GIF,如果我把
L
L
L 拉倒接近
N
N
N 法线,那么
I
I
I 交点就肯定越亮,这个是漫反射的特性,不过这里这么做都是 Gouraud-Phong 的经验模型,真正显示生活中的漫反射是非常复杂的,它是光输入物体内再各种吸收、折射、反射后又从物体内反射出来的光子,非常的复杂,我们只能模拟看起来比较像的效果。
如上图GIF,如果我把
L
L
L 拉倒接近
N
N
N 法线,那么
I
I
I 交点就肯定越亮,这个是漫反射的特性,不过这里这么做都是 Gouraud-Phong 的经验模型,真正显示生活中的漫反射是非常复杂的,它是光输入物体内再各种吸收、折射、反射后又从物体内反射出来的光子,非常的复杂,我们只能模拟看起来比较像的效果。
所以漫反射我自己总结是:迎面的光,就是表面的法线方向越是靠近光源的方向,则该表面越亮。
纯漫反射效果
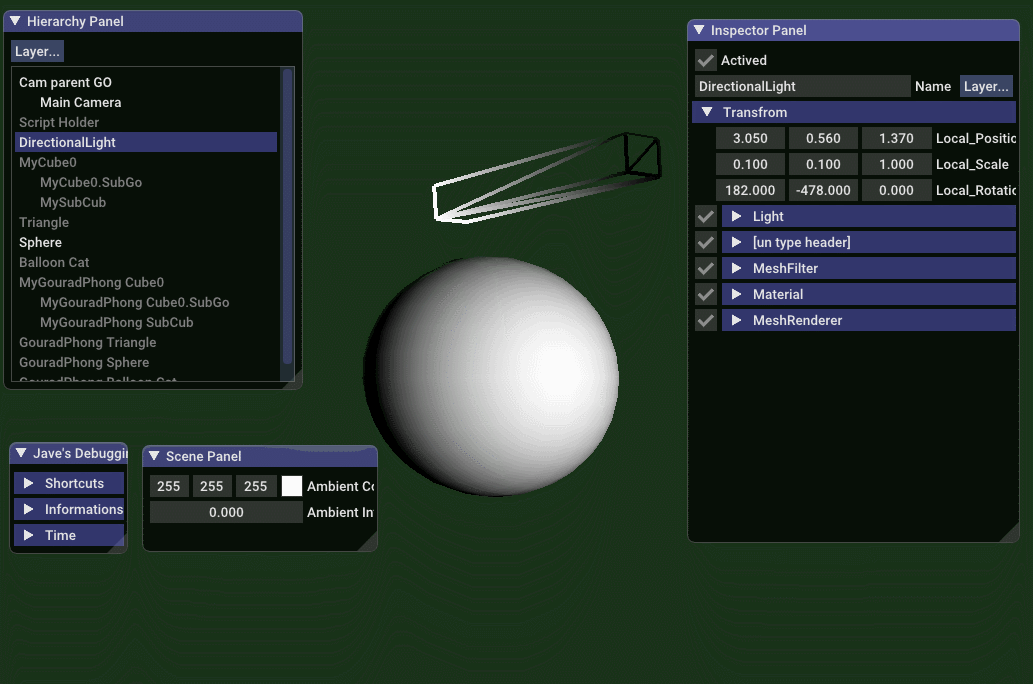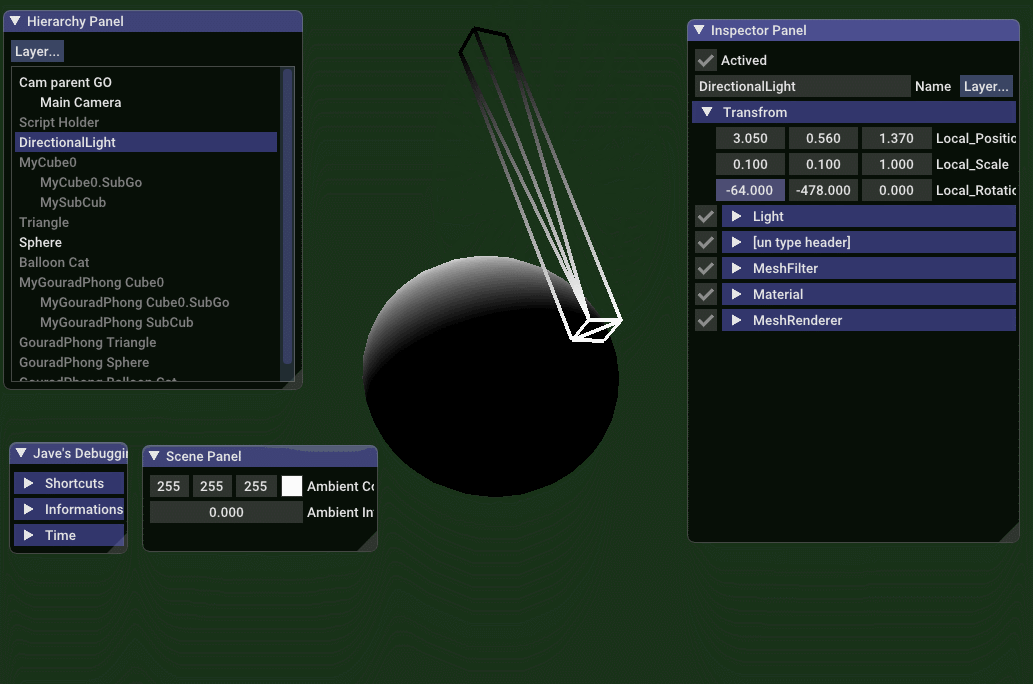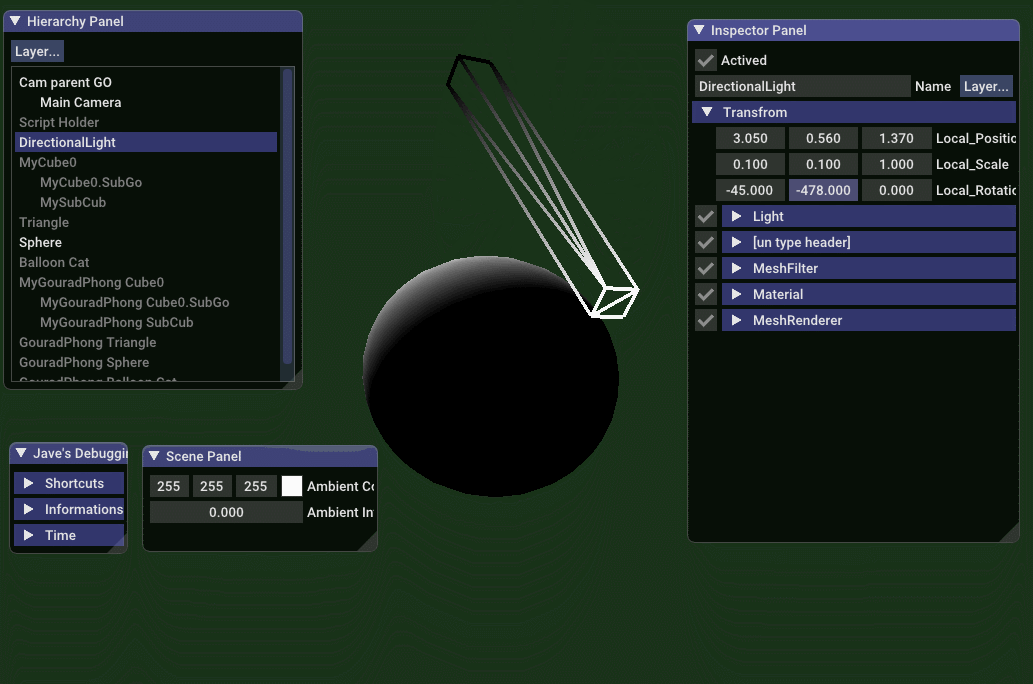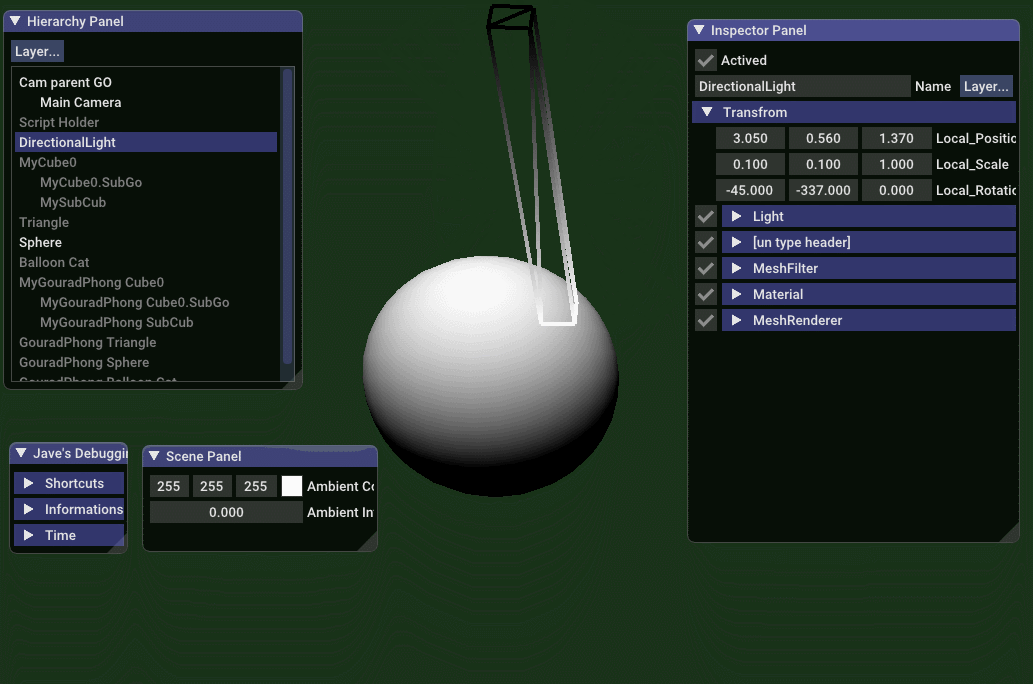
// jave.lin - testing_gouraud_phong_only_diffuse_shading.vert
#version 450 compatibility
// light uniform
uniform vec4 LightPos; // 灯光世界坐标位置,w==0,或名是方向光,w==1说明是点光源,w == 0.5 是聚光灯
// transform matrix uniform
uniform mat4 mMat; // m.v.p 矩阵
uniform mat4 vMat;
uniform mat4 pMat;
uniform mat4 IT_mMat; // model matrix 的逆矩阵的转置
// vertex data
attribute vec3 vPos; // 顶点坐标
attribute vec3 vNormal; // 顶点法线
// vertex data - interpolation
varying vec3 fCol; // 片段插值颜色
// 将对象空间的法线转换到世界空间下的法线
vec3 ObjectToWorldNormal(vec3 n) {
return normalize(mat3(IT_mMat) * n); // 等价于:transpose(I_mMat) * vec4(n, 0)
}
void main() {
vec4 worldPos = mMat * vec4(vPos, 1.0); // 世界坐标
vec3 worldNormal = ObjectToWorldNormal(vNormal); // 获取世界坐标下的法线
float LdotN = dot(LightPos.xyz, worldNormal);
fCol = vec3(LdotN);
// uv0
gl_Position = pMat * vMat * worldPos;
}
// jave.lin - testing_phong_only_diffuse_shading.frag
#version 450 compatibility
// interpolation - 插值数据
varying vec3 fCol; // 片段插值颜色
void main() {
gl_FragColor = vec4(fCol, 1.0);
}
可能你会留意到,我在 ObjectToWorldNormal 函数中注释到:normalize(mat3(IT_mMat) * n) != normalize((IT_mMat * vec4(n,0))) ,这个结果真的是服了。
vec3 ObjectToWorldNormal(vec3 n) {
// return normalize((IT_mMat * vec4(n,0))).xyz; // 等价于:transpose(I_mMat) * vec4(n, 0)
// 下面 normalize(mat3(IT_mMat) * n) 的结果才是正确的, normalize((IT_mMat * vec4(n,0))).xyz 的不正确
// 意思:normalize(mat3(IT_mMat) * n) != normalize((IT_mMat * vec4(n,0))).xyz ,我服了!!!
return normalize(mat3(IT_mMat) * n); // 等价于:transpose(I_mMat) * vec4(n, 0)
}
这个问题,我在 Unity ShaderLabel 可是没有出现这类问题,Unity ShaderLabel 的shader 是类似 HLSL 的,编写起来,比 GLSL 舒服多了。 这个问题,我单独用一篇记录了一下:GLSL 中奇怪的问题 - [已解决] - 自己马虎的问题
这个是我自己的问题,因为在 C++ 层复制代码若的祸,QAQ,因为我在 C++ 有些类似的写法,因为 C++ 里头一次 mat3 转换性能还不如果世界 mat4 * vec4(vec3,0) 的高。
首先:(IT_mMat * vec4(n,0) 求出来的xyzw,中第四个w分量必然是0,这时候再去归一化,就会将第四个分量都算进去,我去!!!竟然写得这么马虎,我服了我自己!
是一种类似镜面反射的现象,用一张图表示的话,可以是这样的: 
specular 就是镜面反射高光系数,但是 GGB 竟然没有pow,或是 power 次幂函数。
所以高光最终系数公式算法模型: S p e c u l a r = p o w ( d o t ( r e f l e c t ( − L , N ) , V ) , g l o s s y ) Specular=pow(dot(reflect(-L,N),V),glossy) Specular=pow(dot(reflect(−L,N),V),glossy)
可以看到也有一个 d o t dot dot,作用与前面的漫反射作用差不多,这里它是求,反射出来的 R R R高光方向与观察者(V,可以理解为眼睛的位置的方向)方向的相似度。意思,越是直接的照射到我们的眼睛的高光系数就越大、高光颜色越亮。
reflect - 反射高光方向这在我们计算 漫反射 与 高光都会用到: I = I a ⋅ K a + ∑ i = 0 n ( I d ⋅ K d ⋅ d o t ( N , L i ) + I s ⋅ K s ⋅ p o w ( d o t ( r e f l e c t ( − L i , N ) , V ) , G l o s s y ) ) I=I_a\cdot K_a+\sum_{i=0}^n(I_d\cdot K_d\cdot \red{dot(N,L_i)} + I_s\cdot K_s\cdot pow(\red{dot(reflect(-L_i,N),V)},Glossy)) I=Ia⋅Ka+∑i=0n(Id⋅Kd⋅dot(N,Li)+Is⋅Ks⋅pow(dot(reflect(−Li,N),V),Glossy)) 中的,高光: d o t ( r e f l e c t ( − L i , N ) , V ) \red{dot(reflect(-L_i,N),V)} dot(reflect(−Li,N),V),这里不管后面的 pow,它是用来调整光泽度的,glossy 就是光泽度的意思。
高光反向是使用 reflect GLSL 函数来实现的。
这里的推导 reflect 公式为: − L i + 2 ⋅ N ⋅ d o t ( N , L i ) -L_i+2 \cdot N \cdot dot(N,L_i) −Li+2⋅N⋅dot(N,Li),但是 GLSL 中 reflect 的公式与我这里列出的不太一样,其实我觉我这个会更方便理解。而且一般处于性能优化,会调整运算元素的位置,原则是:分量相同先处理,例如: − L i + 2 ⋅ N ⋅ d o t ( N , L i ) -L_i+2 \cdot N \cdot dot(N,L_i) −Li+2⋅N⋅dot(N,Li) 和可能会调整为: − L i + 2 ⋅ d o t ( N , L i ) ⋅ N -L_i+2 \cdot dot(N,L_i) \cdot N −Li+2⋅dot(N,Li)⋅N 因为 2 ⋅ d o t ( N , L i ) \red{2 \cdot dot(N,L_i)} 2⋅dot(N,Li) 都是1分量的标量,先运算好它们的结果再与 N N N 向量相乘,运算量即可减少。
GLSL 中的 reflect 的第一个参数是入射角,而我这里的公式是 光源方向。
先画个图会好理解一些:
已知:
N
N
N、
L
L
L 
先是 L i L_i Li(就是图中的L)

然后是
2
⋅
N
2 \cdot N
2⋅N,但这里先不管它,先讲后面的
d
o
t
(
N
,
L
)
dot(N,L)
dot(N,L),还记得它前面说的么?
d
o
t
dot
dot就是求
N
,
L
N,L
N,L量向量的相似度,但这里不是这么理解来使用的,它是当作
cos
(
a
)
\cos(a)
cos(a) 来使用的,它求的是什么?还是再画个图来理解吧: 
d
o
t
(
N
,
L
)
dot(N,L)
dot(N,L) 求的就是
L
L
L 在
N
N
N 上的投影长度,它也是
cos
(
a
)
\cos(a)
cos(a),
d
o
t
(
N
,
L
)
=
邻
边
斜
边
=
∣
N
→
∣
⋅
∣
L
→
∣
⋅
cos
(
a
)
dot(N,L)=\frac{邻边}{斜边}=|\overrightarrow N|\cdot |\overrightarrow L| \cdot \cos(a)
dot(N,L)=斜边邻边=∣N
∣⋅∣L
∣⋅cos(a),邻边就是
∣
N
→
∣
|\overrightarrow N|
∣N
∣ 斜边就是
∣
L
→
∣
|\overrightarrow L|
∣L
∣,因为
∣
N
→
∣
,
∣
L
→
∣
|\overrightarrow N| ,|\overrightarrow L|
∣N
∣,∣L
∣都是1,因为都是单位向量,所以
d
o
t
(
N
,
L
)
=
邻
边
斜
边
=
cos
(
a
)
dot(N,L)=\frac{邻边}{斜边}=\cos(a)
dot(N,L)=斜边邻边=cos(a),所以我们
d
o
t
(
N
,
L
)
dot(N,L)
dot(N,L)求的是
L
L
L 在
N
N
N 方向投影的长度,这个长度值用来缩放
N
N
N向量,那么如下图: 
这个现在与我们的反射角度差不多了,在加多一个
N
⋅
d
o
t
(
N
,
L
)
N\cdot dot(N,L)
N⋅dot(N,L)看看会怎么样?如下图: 
所以现在已经求出了反射向量了,只要我们将原点与这个
−
L
+
N
⋅
d
o
t
(
N
,
L
)
+
N
⋅
d
o
t
(
N
,
L
)
-L+N \cdot dot(N,L)+N \cdot dot(N,L)
−L+N⋅dot(N,L)+N⋅dot(N,L) 的点相连就是反射向量了,如下图:  然后我们的结果是:
−
L
+
N
⋅
d
o
t
(
N
,
L
)
+
N
⋅
d
o
t
(
N
,
L
)
-L+N \cdot dot(N,L)+N \cdot dot(N,L)
−L+N⋅dot(N,L)+N⋅dot(N,L),后面部分有相同的相加,调整为乘法:
−
L
+
2
⋅
N
⋅
d
o
t
(
N
,
L
)
-L+2\cdot N \cdot dot(N,L)
−L+2⋅N⋅dot(N,L),那么这个结果就与我们之前的列出的 reflect 公式一模一样了。
然后我们的结果是:
−
L
+
N
⋅
d
o
t
(
N
,
L
)
+
N
⋅
d
o
t
(
N
,
L
)
-L+N \cdot dot(N,L)+N \cdot dot(N,L)
−L+N⋅dot(N,L)+N⋅dot(N,L),后面部分有相同的相加,调整为乘法:
−
L
+
2
⋅
N
⋅
d
o
t
(
N
,
L
)
-L+2\cdot N \cdot dot(N,L)
−L+2⋅N⋅dot(N,L),那么这个结果就与我们之前的列出的 reflect 公式一模一样了。
但是 GLSL 中的 reflect(-L,N) 总的公式结果与上面的一致,但是公式不一样: GLSL 中的 r e f l e c t ( I , N ) reflect(I, N) reflect(I,N), I I I是入射角,也就是我们上面的 − L -L −L 或是 − L i -L_i −Li
- 我这里的公式是: − L + 2 ⋅ N ⋅ d o t ( N , L ) -L+2\cdot N \cdot dot(N,L) −L+2⋅N⋅dot(N,L)
- GLSL 中公式是: I − 2 ⋅ d o t ( N , I ) ⋅ N I-2 \cdot dot(N,I) \cdot N I−2⋅dot(N,I)⋅N,其中 I = − L I = -L I=−L (也可以参考 CG 的 reflect)
但是结果是一致的,我这里介绍的是灯光方向,GLSL 需要传入的是 光源入射方向,所以我们在使用 GLSL 中的 reflect 需要注意,使用的是 光源入射方向。
但是推导过程原理是一样的,过程的插图我就不发了,有兴趣同学可以自己去尝试。
在 shader 中可以这么使用:
// 第一个参数注意不是入射角
vec3 my_reflect(vec3 L, vec3 N) {
// return -L + 2 * N * dot(N, L);
return -L + 2 * dot(N, L) * N; // 优化调整分量相同先乘
}
// vec3 R = reflect(-LightPos.xyz, worldNormal); // GLSL 内置的 reflect,注意第一个参数是入射角
vec3 R = my_reflect(LightPos.xyz, worldNormal); // 这个是我们根据上面推导的过程编写的
求的了 reflect 的高光反射方向,我们就可以使用 R 与 V(View,观察方向)来求相似度,还记得前面重复强调的 dot 是用来求量向量的相似度的吧?这里我们也是使用它来求 R 与 V 的的相似度。
它们越相似,说明反射光越是直接照射到我们眼球看向的方向的反方向。
留意这个值: 
先看观察位置不变,只改变灯光方向的Specular 高光值效果,看下面的GIF图: 
再看看,只改变观察方向的Specular 高光值效果,看下面的GIF图: 
总结就是如我们上面所述的:只要 R 与 V 方向相似度越高,Specular 高光越大。
纯高光效果
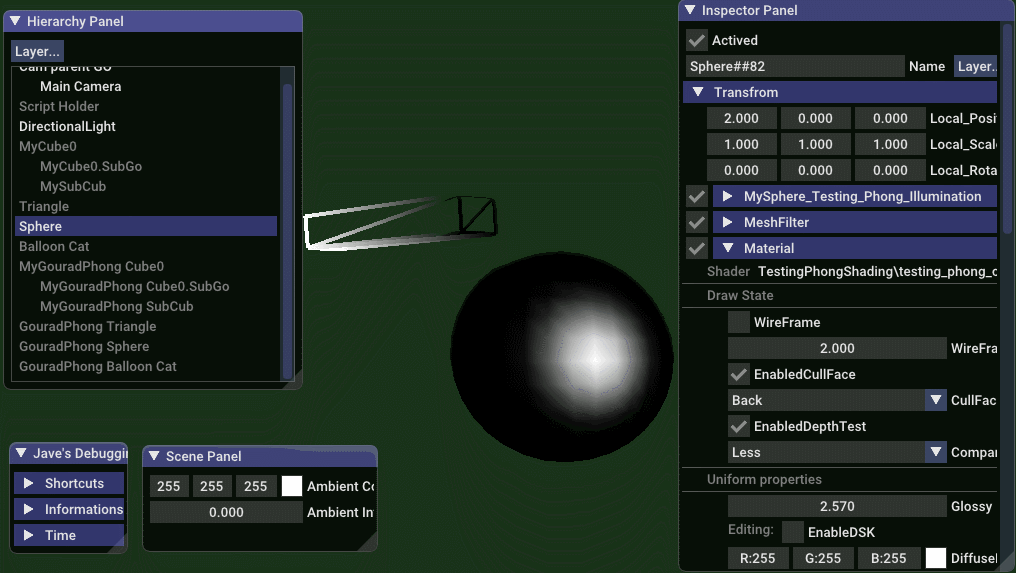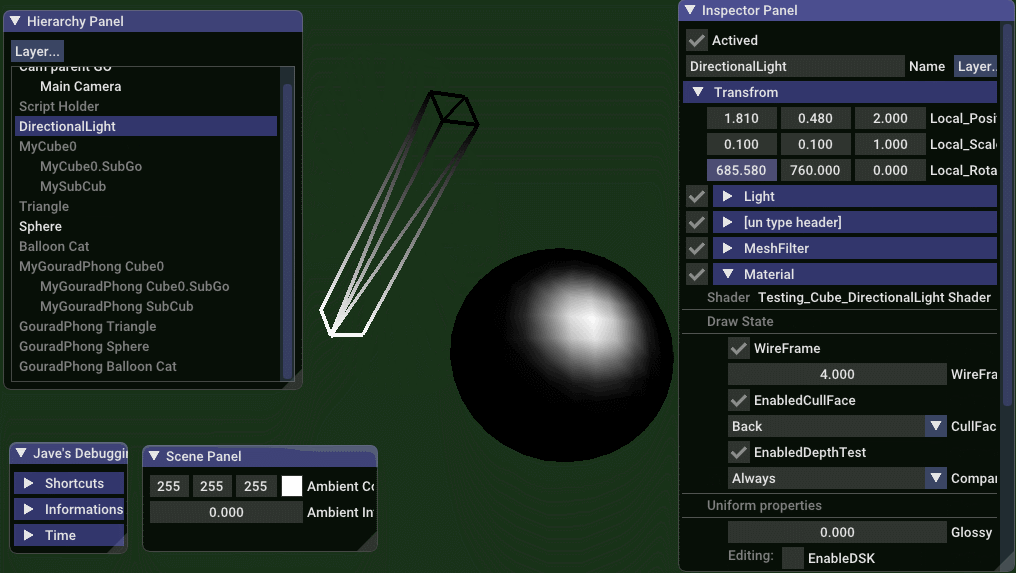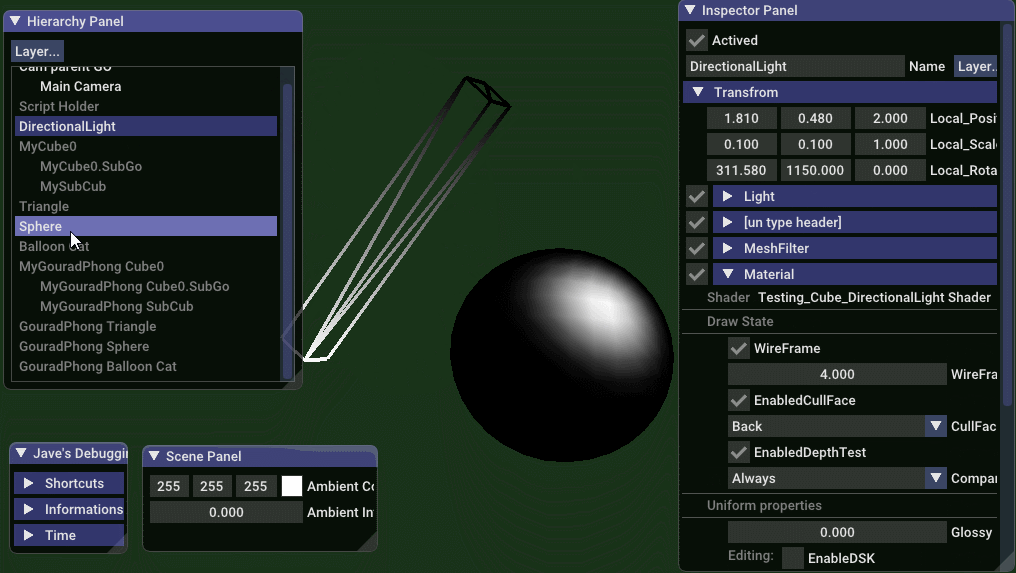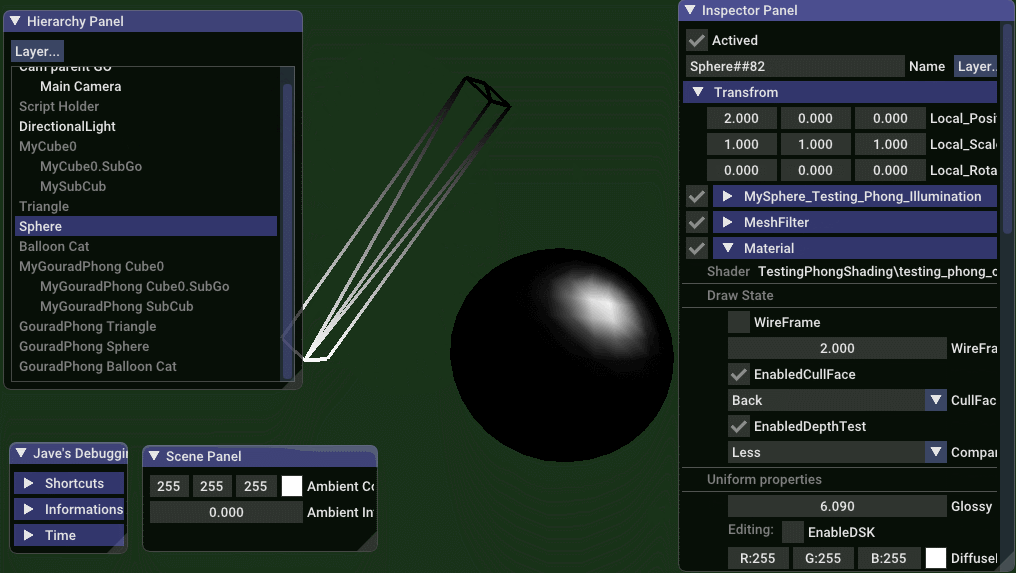
// jave.lin - testing_gouraud_phong_only_specular_shading.vert
#version 450 compatibility
// camera uniform
uniform vec3 _CamWorldPos; // 镜头世界坐标
// object uniform
uniform float Glossy; // 光滑度
// light uniform
uniform vec4 LightPos; // 灯光世界坐标位置,w==0,或名是方向光,w==1说明是点光源,w == 0.5 是聚光灯
// transform matrix uniform
uniform mat4 mMat; // model matrix
uniform mat4 mvpMat; // m.v.p 矩阵
uniform mat4 IT_mMat; // model matrix 的逆矩阵的转置
// vertex data
attribute vec3 vPos; // 顶点坐标
attribute vec3 vNormal; // 顶点法线
// vertex data - interpolation
varying vec3 fCol; // 片段插值颜色
// 将对象空间的法线转换到世界空间下的法线
vec3 ObjectToWorldNormal(vec3 n) {
return normalize(mat3(IT_mMat) * n); // 等价于:transpose(I_mMat) * vec4(n, 0)
}
vec3 my_reflect(vec3 L, vec3 N) {
// return -L + 2 * N * dot(N, L);
return -L + 2 * dot(N, L) * N; // 优化调整分量相同先乘
}
void main() {
vec3 worldPos = (mMat * vec4(vPos, 1.0)).xyz; // 世界坐标
vec3 worldNormal = ObjectToWorldNormal(vNormal); // 获取世界坐标下的法线
vec3 viewDir = normalize(_CamWorldPos - worldPos); // 顶点坐标 指向 镜头坐标 的方向
float LdotN = dot(LightPos.xyz, worldNormal);
// vec3 R = reflect(-LightPos.xyz, worldNormal); // 注意内置的是用入射角
vec3 R = my_reflect(LightPos.xyz, worldNormal); // 注意我们自己编写的 reflect 是灯光方向
float RdotV = max(0, dot(R, viewDir));
float S = 0;
if (LdotN > 0) {
S = pow(RdotV, Glossy);
}
fCol = vec3(S);
// uv0
gl_Position = mvpMat * vec4(vPos, 1.0);
}
// jave.lin - testing_gouraud_phong_only_specular_shading.frag
#version 450 compatibility
// interpolation - 插值数据
varying vec3 fCol; // 片段插值颜色
void main() {
gl_FragColor = vec4(fCol, 1.0);
}
先看效果图,下面是实时调整平行方向光的 方向,强度 和 灯光颜色 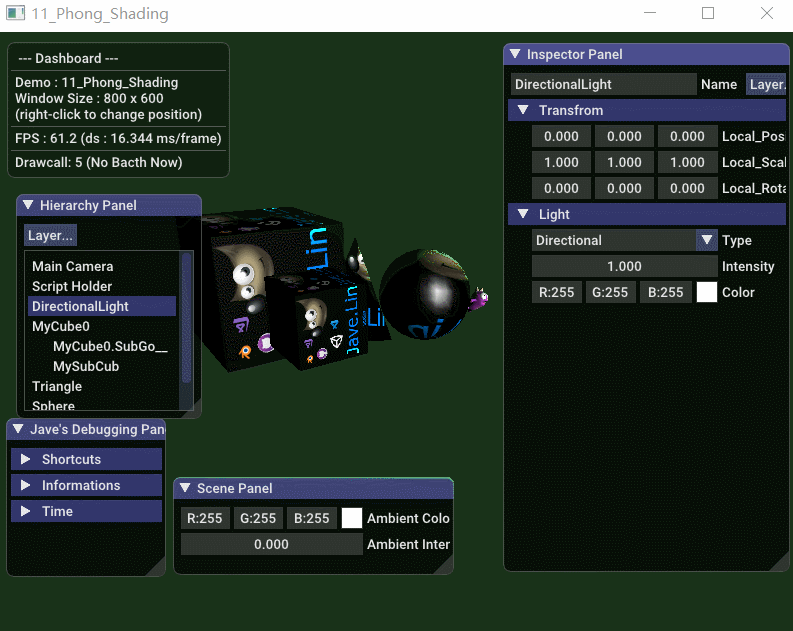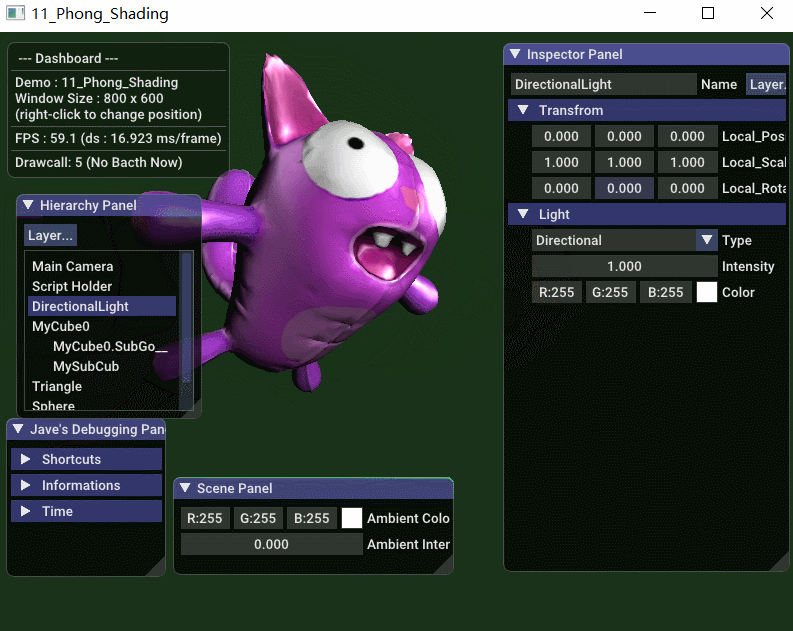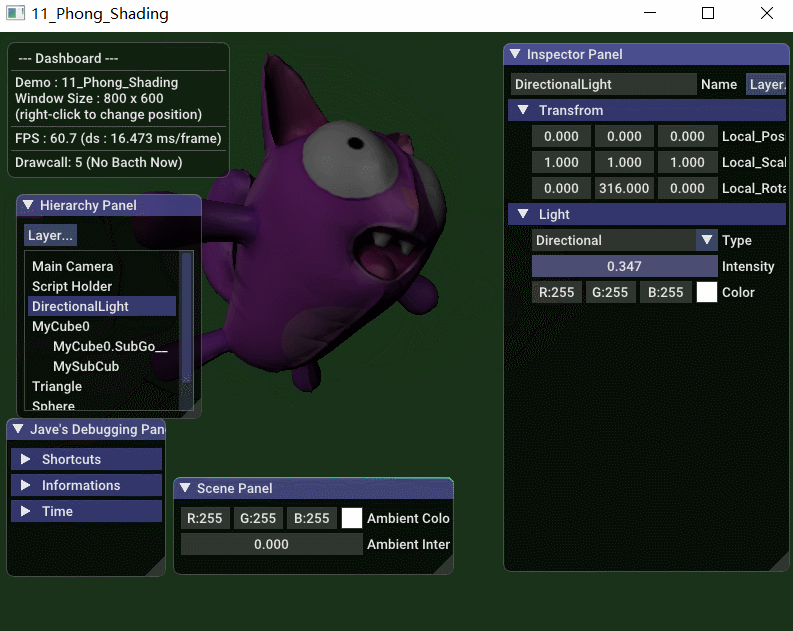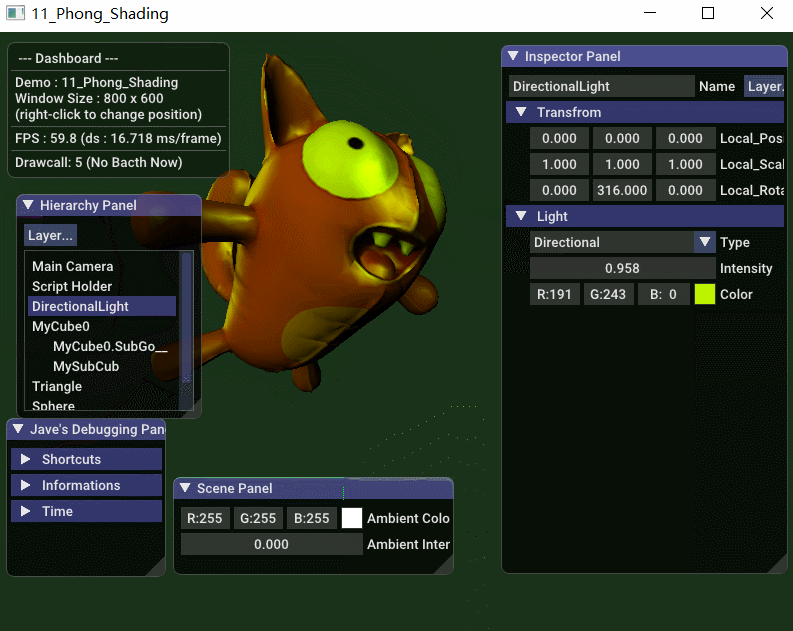 从 Gouraud 光照模型公司可得知:
I
=
I
a
⋅
K
a
+
∑
i
=
0
n
(
I
d
⋅
K
d
⋅
d
o
t
(
N
,
L
i
)
+
I
s
⋅
K
s
⋅
p
o
w
(
d
o
t
(
r
e
f
l
e
c
t
(
−
L
i
,
N
)
,
V
)
,
G
l
o
s
s
y
)
)
I=I_a\cdot K_a+\sum_{i=0}^n(I_d\cdot K_d\cdot dot(N,L_i) + I_s\cdot K_s\cdot pow(dot(reflect(-L_i,N),V),Glossy))
I=Ia⋅Ka+∑i=0n(Id⋅Kd⋅dot(N,Li)+Is⋅Ks⋅pow(dot(reflect(−Li,N),V),Glossy)),除了有漫反射、高光,还有一个:环境光。
从 Gouraud 光照模型公司可得知:
I
=
I
a
⋅
K
a
+
∑
i
=
0
n
(
I
d
⋅
K
d
⋅
d
o
t
(
N
,
L
i
)
+
I
s
⋅
K
s
⋅
p
o
w
(
d
o
t
(
r
e
f
l
e
c
t
(
−
L
i
,
N
)
,
V
)
,
G
l
o
s
s
y
)
)
I=I_a\cdot K_a+\sum_{i=0}^n(I_d\cdot K_d\cdot dot(N,L_i) + I_s\cdot K_s\cdot pow(dot(reflect(-L_i,N),V),Glossy))
I=Ia⋅Ka+∑i=0n(Id⋅Kd⋅dot(N,Li)+Is⋅Ks⋅pow(dot(reflect(−Li,N),V),Glossy)),除了有漫反射、高光,还有一个:环境光。
环境光 的计算非常简单,只是颜色*强度的结果相加到最终颜色的输出即可,但是效果不太好,具体可以参考下面的 Shader 代码
Normal - 法线上面所说的法线(Normal),是怎么来的呢,在我的 Cube 的模型中,我们是通过程序计算出来的,我们可以通过三角面的三个点来计算出发现,这与左右手坐标有光,也与三角面顶点顺序有光。
发现如何求得,可以查考我之前的文章:
- Unity Shader - Billboard 广告板/广告牌 - 向量叉乘顺序
(其实我之前的软光栅器也有类似的处理)
在 C++ 的 LearnGL 系列笔记的项目中,我也重写了一个版本:
void Mesh::recalculateNormal() {
if (_vertices == NULL || _indices == NULL) return;
DESTROY(_normals);
size_t pos_count = _vertices->size() / 3;
size_t arr_count = pos_count * 3;
GLfloat* normals_data = (GLfloat*)malloc(sizeof(GLfloat) * arr_count);
//GLfloat* normals_data = new GLfloat[arr_count];
// fill normals here,目前这里只支持三角形
vec3 pos0, pos1, pos2;
for (size_t i = 0; i size(); i += 3) {
GLuint idx0 = _indices->at(i + 0);
GLuint idx1 = _indices->at(i + 1);
GLuint idx2 = _indices->at(i + 2);
pos0.x = _vertices->at(idx0 * 3 + 0);
pos0.y = _vertices->at(idx0 * 3 + 1);
pos0.z = _vertices->at(idx0 * 3 + 2);
pos1.x = _vertices->at(idx1 * 3 + 0);
pos1.y = _vertices->at(idx1 * 3 + 1);
pos1.z = _vertices->at(idx1 * 3 + 2);
pos2.x = _vertices->at(idx2 * 3 + 0);
pos2.y = _vertices->at(idx2 * 3 + 1);
pos2.z = _vertices->at(idx2 * 3 + 2);
vec3 normal = glm::normalize(glm::cross(pos1 - pos0, pos2 - pos0));
memcpy(normals_data + (idx0 * 3), glm::value_ptr(normal), sizeof(vec3));
memcpy(normals_data + (idx1 * 3), glm::value_ptr(normal), sizeof(vec3));
memcpy(normals_data + (idx2 * 3), glm::value_ptr(normal), sizeof(vec3));
//std::cout
关注
打赏
最近更新
- 深拷贝和浅拷贝的区别(重点)
- 【Vue】走进Vue框架世界
- 【云服务器】项目部署—搭建网站—vue电商后台管理系统
- 【React介绍】 一文带你深入React
- 【React】React组件实例的三大属性之state,props,refs(你学废了吗)
- 【脚手架VueCLI】从零开始,创建一个VUE项目
- 【React】深入理解React组件生命周期----图文详解(含代码)
- 【React】DOM的Diffing算法是什么?以及DOM中key的作用----经典面试题
- 【React】1_使用React脚手架创建项目步骤--------详解(含项目结构说明)
- 【React】2_如何使用react脚手架写一个简单的页面?



