目录
1. 插入排序的缺点
- 1. 插入排序的缺点
- 2. 希尔排序的介绍
- 3. 希尔排序的程序实现(交换法)
- 4. 希尔排序的程序实现(移动法)
一种极端的情况:当一个最小的数,位于无序表的最后,则在最后一轮遍历时,则需要后移n -1次之后,才能将这个最小的数,插入到有序表的第一个位置。效率太低
2. 希尔排序的介绍希尔排序也是一种插入排序,是对简单插入排序算法的改良,也称缩小增量排序
希尔排序法基本思想:希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序。随着增量(分组)逐渐减少,每组包含的元素越来越多,当增量(分组)减至1时,算法便终止。如下所示
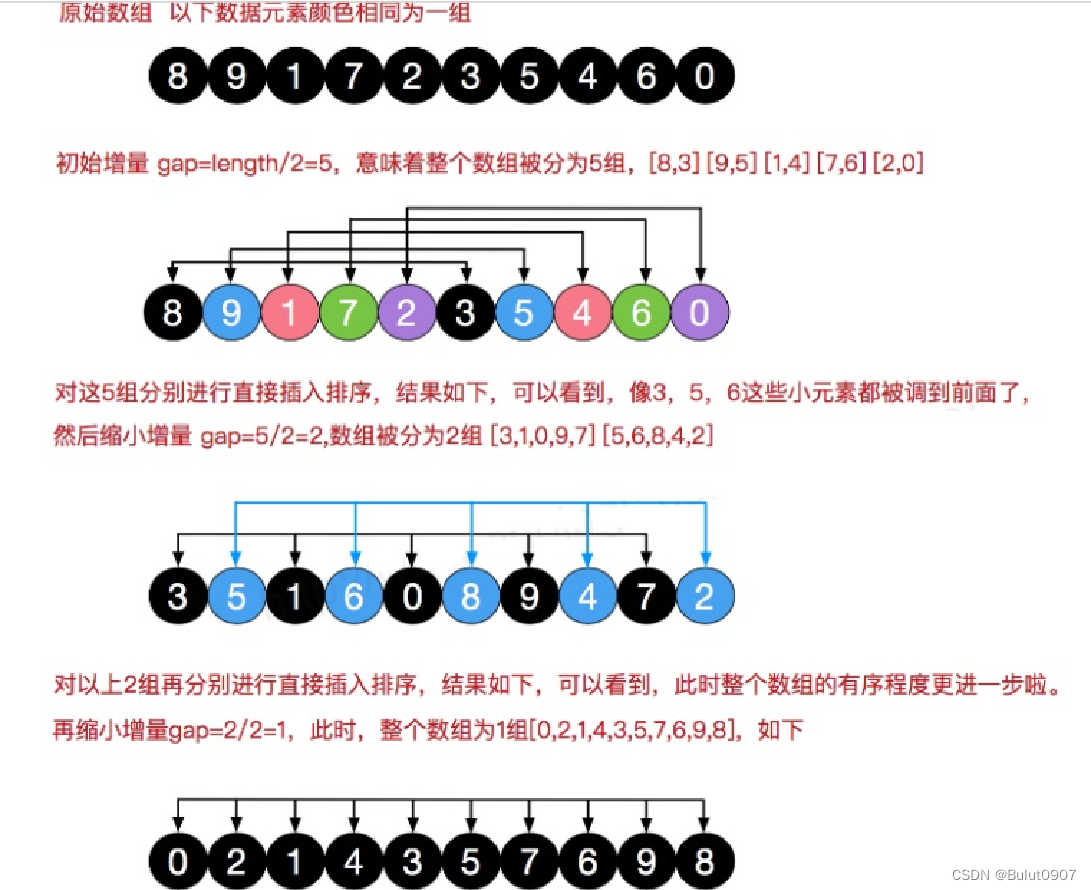 再对上面的数列进行简单的微调,无需大量移动操作即可完成整个数组的排序
再对上面的数列进行简单的微调,无需大量移动操作即可完成整个数组的排序
需求:有一组无序的数据{8, 9, 1, 7, 2, 3, 5, 4, 6, 0}; ,请用对有序序列在插入时采用交换法的希尔排序算法实现从小到大排列
程序如下:
import java.util.Arrays;
public class ShellSort {
public static void main(String[] args) {
int[] exchangeArray = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
//交换法
exchangeShellSort(exchangeArray);
System.out.println(Arrays.toString(exchangeArray));
}
// 对有序序列在插入时采用交换法的希尔排序算法
public static void exchangeShellSort(int[] array) {
int tmp = 0;
// 用于控制进行多少种方式的分组
for (int gap = array.length / 2; gap > 0; gap /= 2) {
// 用于控制在一种方式的分组中,所有组共需要遍历多少轮(会遍历每组除第一个元素的所有元素)
for (int i = gap; i < array.length; i++) {
// 在一轮中,对该组中当前元素和前面所有元素依次进行大小比较
for (int j = i - gap; j >= 0; j -= gap) {
// 如果大的在前面,则将大的交换到后面去
if (array[j] > array[j + gap]) {
tmp = array[j];
array[j] = array[j + gap];
array[j + gap] = tmp;
}
}
}
}
}
}
运行程序,结果如下:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
需求:有一组无序的数据{8, 9, 1, 7, 2, 3, 5, 4, 6, 0}; ,请用对有序序列在插入时采用移动法的希尔排序算法实现从小到大排列
程序如下:
import java.util.Arrays;
public class ShellSort {
public static void main(String[] args) {
int[] moveArray = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};
//移动法
moveShellSort(moveArray);
System.out.println(Arrays.toString(moveArray));
}
// 对有序序列在插入时采用移动法的希尔排序算法
public static void moveShellSort(int[] array) {
int tmp = 0;
// 用于控制进行多少种方式的分组
for (int gap = array.length / 2; gap > 0; gap /= 2) {
// 用于控制在一种方式的分组中,所有组共需要遍历多少轮(会遍历每组除第一个元素的所有元素)
for (int i = gap; i < array.length; i++) {
int j = i;
tmp = array[j];
// 在一轮中,对该组中当前元素和前面的所有元素依次进行比较(前面的所有元素已经有序)
// 然后以插入(移动法)的方式,将当前元素插入到适合的位置
while (j - gap >= 0 && tmp < array[j - gap]) {
// 移动法
array[j] = array[j - gap];
j -= gap;
}
array[j] = tmp;
}
}
}
}
运行程序,结果如下:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]



