FPGA：实现快速傅里叶变换（FFT）算法

前言

第一次使用FPGA实现一个算法，搓手手，于是我拿出一股势在必得的心情打开了FFT的视频教程，看了好几个视频和好些篇博客，于是我迷失在数学公式推导中，在一位前辈的建议下，我开始转换我的思维，从科研心态转变为先用起来，于是我关掉我的推导笔记，找了一篇叫我用Verilog写FFT的视频B站 - 使用Verilog写FFT，跟着他先让代码跑起来，然后再择需深入

使用软件：vivado 实现算法：N=8的FFT算法 大框架：使用并行的3级流水线

正文

以下内容以快速让FFT代码跑起来为出发点，所以不会有复杂的理论推导，如果想要深入研究，可参考网上的详细教程，以下我会介绍我实现的过程，如果下面内容有误，请一定帮我指出

一、如何用FPGA实现FFT

在这里我们先直接抛出在FPGA里面是如何实现FFT的，然后再逐次推进涉及到的内容

1.1 实现FFT的核心

核心就是用Verilog代码写出下面的这幅图 可能你和我一样一开始不知道 怎么下手，连这个图都看不懂，没关系！！我们一步步来 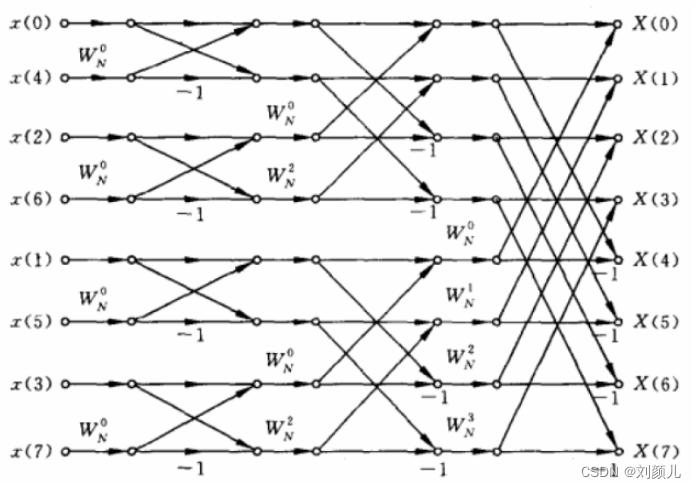有了目标，就围绕着我们的目标进行知识补充，（这样以目标为导向，不至于迷失在数学公式推导中） 首先我们要知道这个图是个啥，推荐看这个老师的视频，视频时长很短，只需要十多分钟就能对这幅图有个初步的认识 推荐视频：B站-潘老师-数字信号处理

需要明确的地方：

1. 上面的图叫：蝶形图
2. W N 0 = 1 W_{N}^{0}=1 WN0​=1
3. 最左侧是时域，最右侧是 频域

以下是我看了视频后做的笔记：

这个口诀可以等你看完视频和我下面的笔记后，用来作为帮助记忆的辅助材料 口诀： 箭尾出发，箭头停 箭身有值要乘上 每次走完2支箭 箭身长的写在前

首先最左侧的 x ( 0 ) , . . . , x ( 7 ) x(0),...,x(7) x(0),...,x(7) 从箭尾出发，箭身上有值的就和上面的值相乘，每次只能走完2个箭就要停下来计算一次值，并且从斜着的箭过来的值写在计算表达式的第一位，直着过来的值写在计算表达式的第二位 先挖个坑，等有空录一个简单的视频说一说这个蝶形图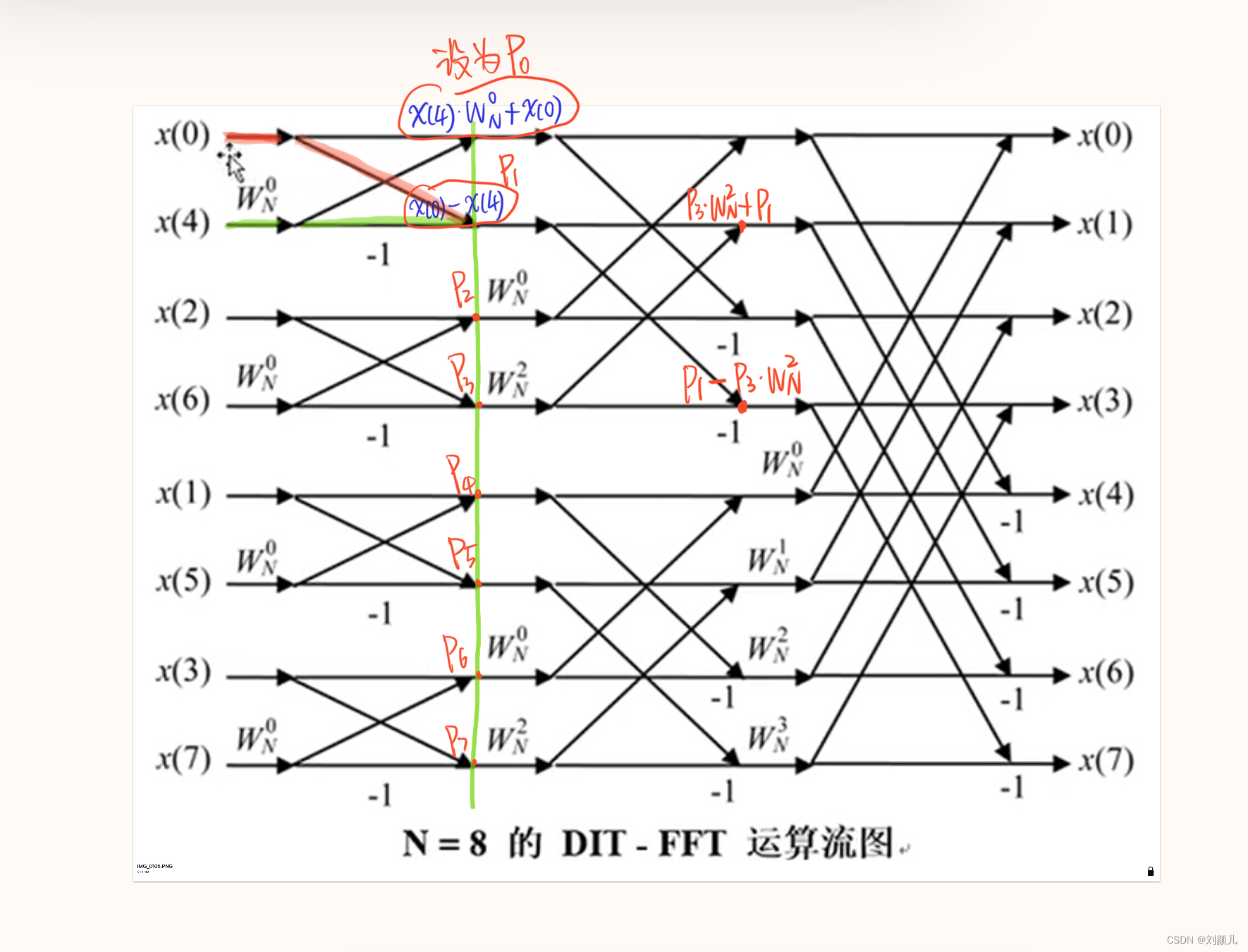

1.2 蝶形图的组成元素

蝶形图无非就是一些元素构成的：左右两边的 $x$ , $W_{N}^{0}$ , $W_{N}^{1}$ , $W_{N}^{2}$ , $W_{N}^{3}$, -1,还有一些箭头，以及图下面图例中 $N=8$ 只要我们知道这些元素是啥，用来干什么就能大概看懂蝶形图了

1.2.1 旋转因子 W N W_{N} WN​

快速傅里叶变换（FFT）是对离散傅里叶变换（DFT）的一种加速算法，FFT比DFT运算速度快的原因，就是这个旋转因子的功劳。 旋转因子的表达式如下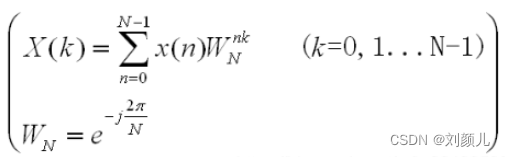： 旋转因子有一些比较好的性质：周期性、可约性、对称性，个人认为如果不做公式推导，那就知道它的这些性质即可 在下面的代码中，第二级流水线里的例化复数乘法IP核时，我们直接将旋转因子给出（如下的倒数第三行）

// 复数乘法的IP核，求解与旋转因子的乘积
cmpy_0 cmpy23(
    .aclk(clk),
    .s_axis_a_tvalid(fft1_en),
    .s_axis_a_tdata({4'd0, fft1_im3,1'd0,4'd0, fft1_re3,1'd0}),//乘法元素中的复数：既有实部又有虚部
    .s_axis_b_tvalid(1'b1),
    .s_axis_b_tdata({8'd0,8'b10110101,8'd0,8'b10110101}),// 旋转因子
    .m_axis_dout_tvalid(fft2_en1),
    .m_axis_dout_tdata(fft2_cmpy23)
    );

1.2.2 输入数据倒序排列

可能有细心的朋友会发现，蝶形图左边的 x x x 的排序不是按照升序或降序拍的，而是将 0 − 7 0-7 0−7 的二进制写出来后，将二进制的高位、低位互换后得到的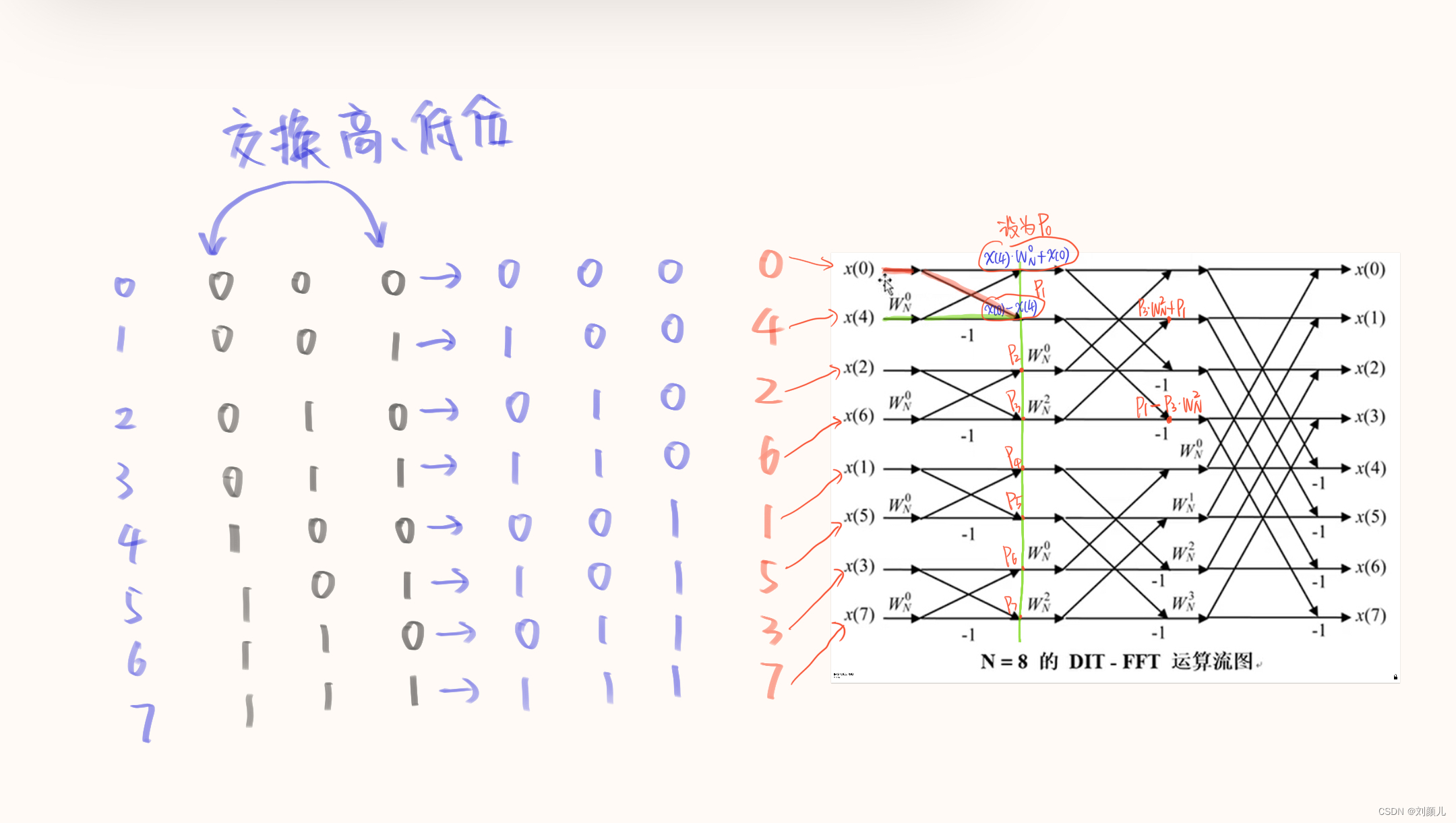

1.2.3 N是什么

目前蝶形图中的元素只剩下这个图例中的 N = 8 N=8 N=8 了，这里的 N N N 表示每一列的点数，虽然蝶形图中有很多点，但是每一列都只有8个点， l o g 2 N log_{2}N log2​N= 每组的蝶形次数，这里 N = 8 N=8 N=8，每组就要做4次蝶形

我在看教程时，还会看到基-2、基-4这样的名词， N N N 还可以用来区分这两个名词（虽然我不知道区分这俩有啥用）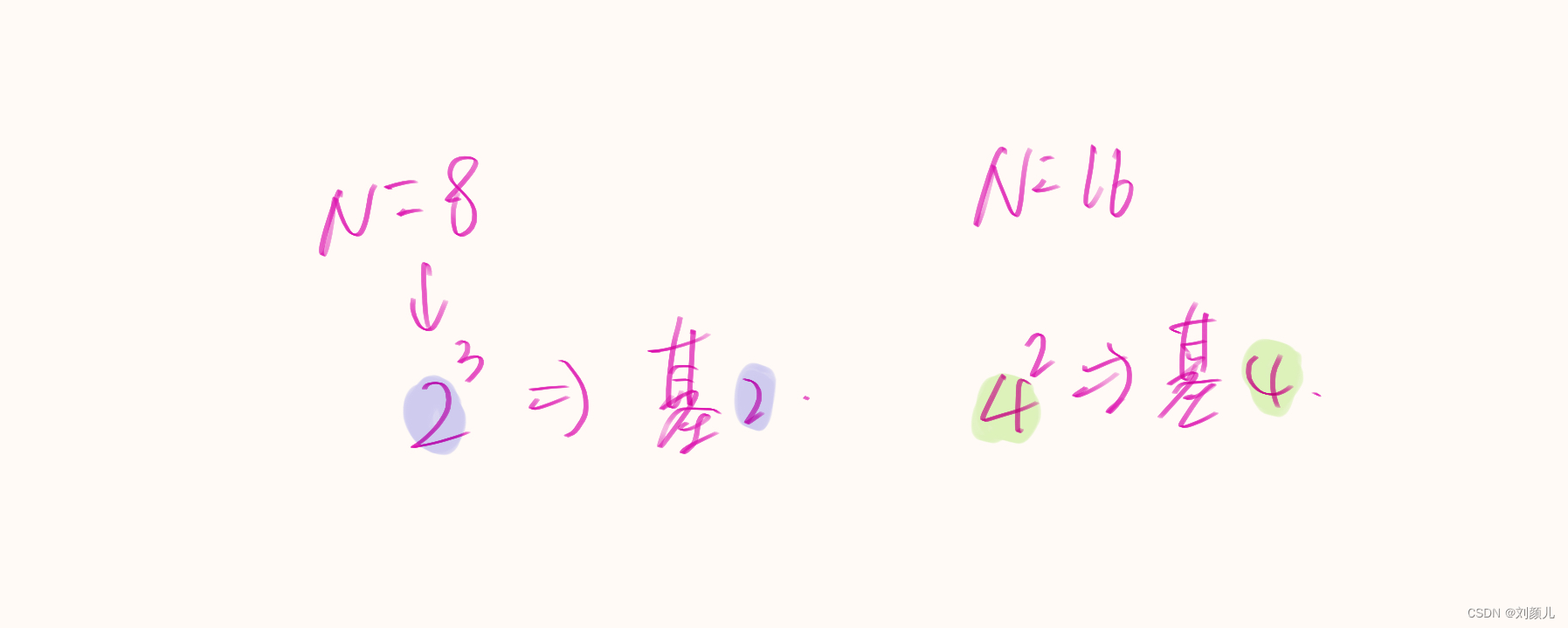

1.3 Verilog编写蝶形图

从图中可以看到，处理N=8这样的蝶形图，分3步走，即可以使用3级流水线来实现

1.3.1 第一级流水线

always @(posedge clk or negedge rst_n)begin
    if(!rst_n)
        begin
            fft1_en