在我的另一篇文章中,我简单的介绍了向量的点积,也叫内积。那篇文章的侧重点是点积或者说是点乘。主要是以的方式来定义两个向量的内积。而这篇文章我会见到内积的另外一种表示方式,从
变成了
。
线性代数 --- 内积(点积)(个人学习笔记)_松下J27的博客-CSDN博客向量与向量的乘法 - 内积两个向量的内积,也叫点积(但在我们这个笔记的前半部分,我们说的,或者用到的更多的应该是点积),他的计算方式是两个同维度向量(例如两个n维向量)的内部元素从1到n,逐一相乘再求和,得到的是一个数。注意,这里是两个2x1的向量,而不像我们之前的定义内积等于一个1xn的向量乘以一个nx1的向量,他是用下面的这种表示法表示的。两个相互垂直的向量内积为0 如果两个向量的点积为0,则他们的夹角是90度。就如上图中的w,...https://blog.csdn.net/daduzimama/article/details/124556809
在这篇文章中,我们已经知道了两个向量x,y的点积等于的累加和。而在这个文章里,我们不再用之前的那个“不专业的点乘”来描述点积了,而是用矩阵的方式来描述:

如果说,x,y都是nx1的列向量,那么计算内积的公式就变成了,这是一个1xn的行向量和一个nx1的列向量的乘积,其中T在x和y外的内部,叫内积。而外积,也就是
,是一个nx1的列向量和一个1xn的行向量的乘积,T在x和y的外部。
内积的结果是一个数。
外积的结果是一个矩阵。
这种用矩阵的方式来描述内积的方式,把求两个向量的内积和矩阵的转置,这两个看似毫无关系的事,紧密的联系在了一起。要知道,之前我们在定义矩阵的转置时,只是把他简单的定义为将矩阵A中的元素沿着主对角线翻过去就行了,A的行变成了的列,而A的列变成了
的行。即:
事实上,转置有一种更深刻的含意,这源于它与内积有着密切的联系。而这种联系可以被用来给出转置的一个全新的定义(这是一种非常抽象的定义):
对于任何向量x,y,矩阵能保证下面等式两边的两个内积相等。
![]()
也就是说,Ax与y的内积等于x与y的内积。
![]()
转置的这种定义有两个含义:
1,它告诉我们,当我们用其他方式来定义内积时,转置应该怎么变动。
2,它能够被用于证明转置矩阵的一个重要性质:
(一式)
证明:对于第二个等式的证明,只需要把AB作为一个整体带入到上面蓝色定义的等式中去,同时运用这个定理两次。

![]()
举个例子:
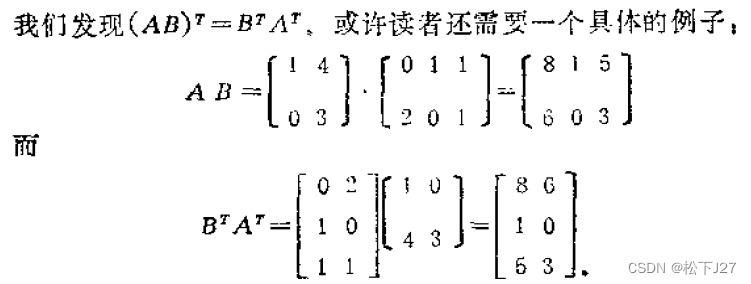
这是外文教科书中的另外一个例子:
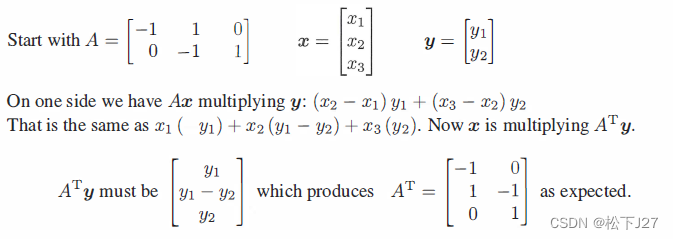
注意:转置矩阵的这个性质和逆矩阵的性质如出一辙:
(二式)
而把一式和二式放在一起,就能得到另外一个著名的公式:
(全文完)
作者 --- 松下J27
格言摘抄:凡 事 都 有 定 期 , 天 下 萬 務 都 有 定 時 。《传道书》3章1节
鸣谢:
文中截图均来自于:《Introduction to Linear Algebra》,5th Edition - Gilbert Strang

(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27



