
例一:

因为,w1与w2线性无关,且二者的第三分量都是0,所以只能张成一个二维平面。又因为w1和w2都是三维向量,所以,是三维空间中的一个二维平面。w1和w3线性相关,又都只有第一个分量起作用,所以只能张成一条直线。
例二:


基底不唯一:
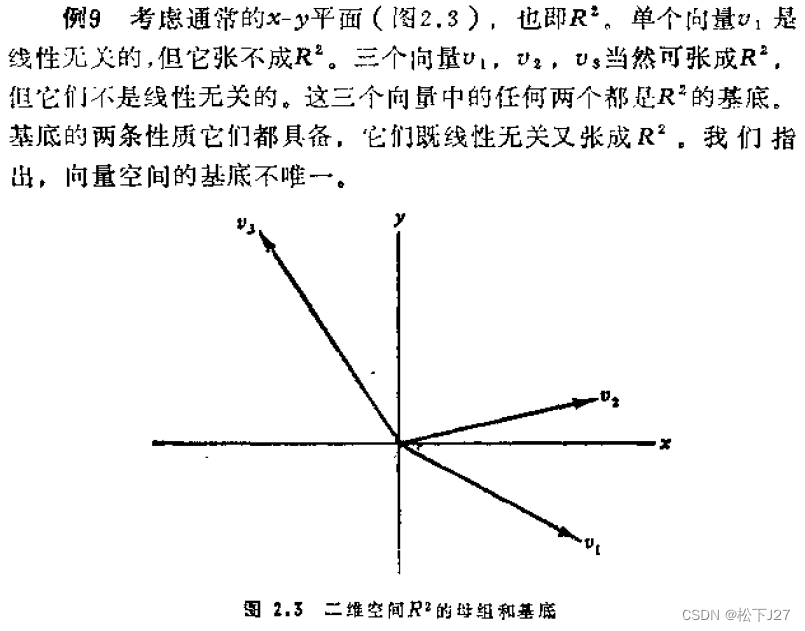
例一:

例10中的列空间属于R3,却因为只存在两个非零主元列,所以是R3的二维子空间。
维数:
就这个定理而言,单从字面意思上去理解,向量空间V的维数,等于该向量空间中,任意一个基底所包含的元素个数。例如,在x-y平面,他的可能的一组基底是[0 1],[1 0]。这两个基底中的任意一个基底的元素个数都是两个,因此,向量空间的维数是2,即二维。
补充:
考虑上面的这个矩阵,已知,A为2x3矩阵,秩r=2。求A或U的列空间:
一方面,列空间的一组基底为[1 0]',[0 1]',A的列空间是各列的线性组合,当然也是基底的线性组合。基底中的列向量所包含的元素个数为2。因此,列空间的维度为2。另一个方面,根据线性代数中关于四个基本子空间的相关定理,A的列空间的维度等于秩r,等于A中所有线性无关的列向量的个数2。(注意,这里说的是向量的个数,而不是向量中元素的个数,或者说向量的维度)
可见,A的列空间分别从两个角度去理解,得到了相同的维度2。A的列空间充满了整个空间。
对于A的行空间而言,一方面,行空间的基底为[1 0 0],[0 1 0]共两个行向量,每个行向量包含的元素个数为3。因此,行空间的维度为3。另一方面,A的行空间的维度等于A的秩,又因为,列秩等于行秩,等于A中线性无关行的个数。得出,A的行空间的维数是2。
不矛盾:秩永远小于等于min(m,n),所以,用第二种方式求得的维数要么是第一种方式求得的维数的子空间,要么就能充满全部空间。
(全文完)
作者 --- 松下J27
鸣谢(参考文献):
1,《Introduction to Linear Algebra》,5th Edition - Gilbert Strang
2,线性代数及其应用,侯自新,南开大学出版社,1990.
格言摘抄:八戒,八戒,心肠不坏。(天上掉下个猪八戒主题曲)

(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27



