数字信号处理 --- 用离散傅里叶变换(循环卷积)实现线性卷积（个人学习笔记）

时域的循环卷积等于频域的离散傅里叶变换，离散傅里叶变换DFT是离散傅里叶级数DFS的一个周期，离散傅里叶级数DFS是对连续时间傅里叶变换CTFT的采样

离散傅里叶级数DFS

         周期为10的方波信号的傅里叶级数，以10为周期向两边无限复制拓展信号的傅里叶级数。

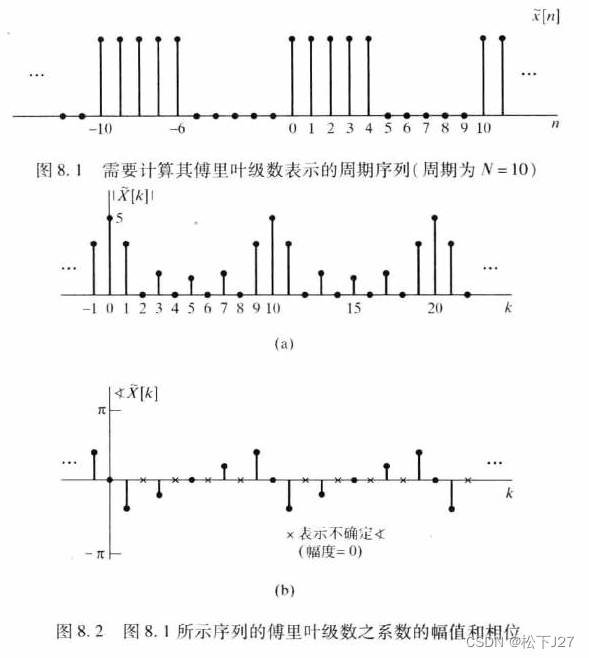
         注意上图中x[n]上面的“~”号，那个就是周期函数的意思。以N为周期的周期信号在0~N-1这一个周期内等于x[n]。

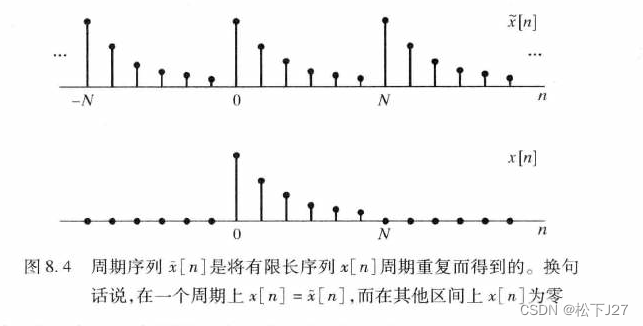
 离散傅里叶级数DFS的系数是对离散傅里叶变换DFT的采样：

        对一个离散非周期序列x[n]的傅里叶变换采样的结果等于，将x[n]无限周期重复而得到的一个周期信号的离散傅里叶级数DFS的系数。 

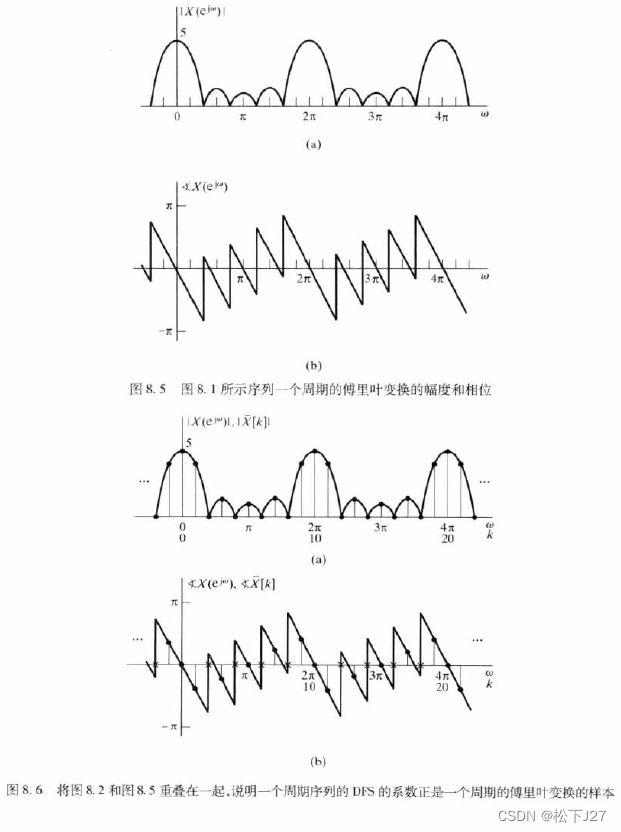
离散傅里叶级数DFS的系数等同于对Z变换单位圆上的采样（傅里叶变换等于z变换单位圆上的值）：

         若，周期序列的周期为N，那么与之对应的对傅里叶变换进行采样的间隔为2Pi/N。

循环卷积circular convolution

        线性卷积：x1和x2分别是两个长度为6的方波信号，x3是他们的线性卷积，线性卷积的长度为L+P-1=11.

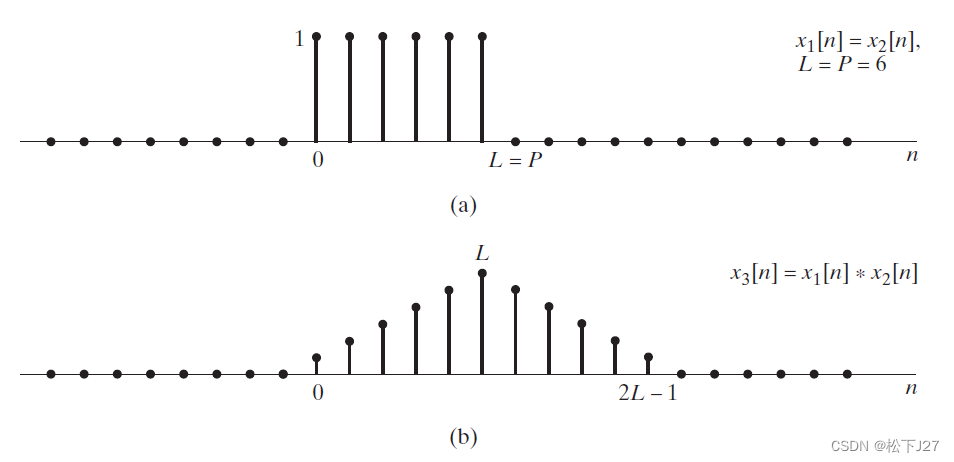
        N点的循环卷积：图c和图d分别是线性卷积的结果x3，向左和向右移动6个单位的结果。而,图e和图f，分别是N=6点的循环卷积和N=12点的循环卷积的结果。

        可见，对于N=6点的循环卷积，图e，来说，循环卷积的结果等于b(x3[n]),c(x3[n-N]),d(x3[n+N])，在区间n=0~N-1上的和。此时，循环卷积的点数N=L+P-1。

 

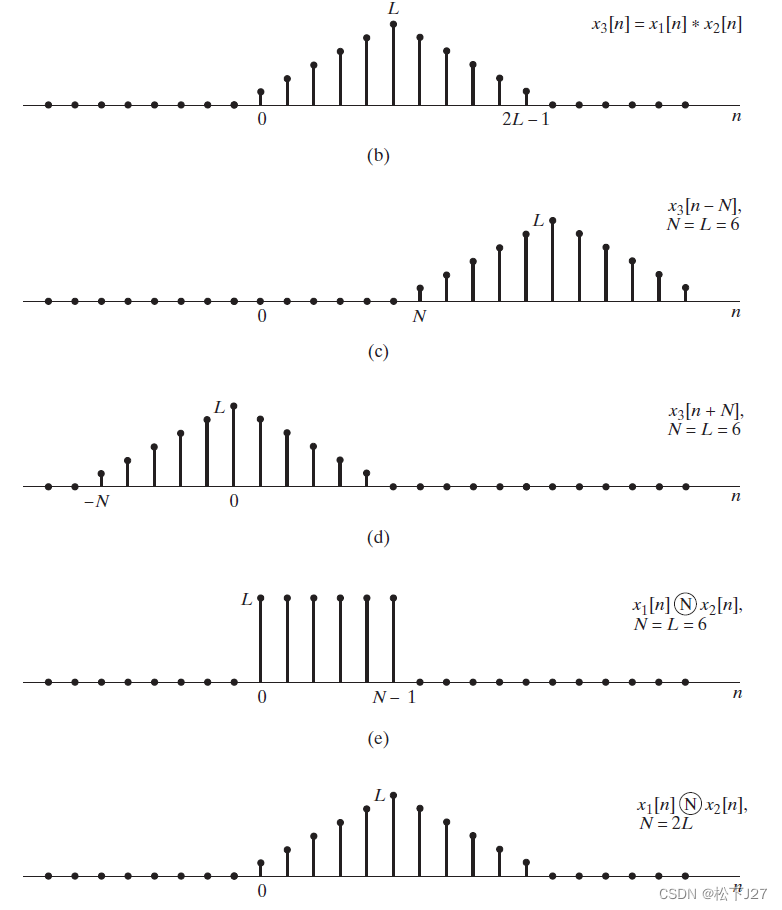
         上图说明，对于N个点的循环卷积，当N=L=P时，循环卷积的结果完全不同于线性卷积。当N>=L+P-1时，循环卷积的结果正好等于线性卷积，这时没有发生混叠。但是，对于长度不同的两个信号P