- 前言
- 文章中心思想
- 全文概览
- 系统模型
- 大规模天线点对点MIMO系统的场景
- 大规模天线MU-MISO系统的场景
- 仿真结果
- MIMO系统下的HBF性能
- MU-MISO下的HBF性能
- 相关阅读
混合波束赋形专栏|基于坐标迭代更新法的混合波束赋形算法:整理2016年一篇JSAC高引论文中的混合波束赋形算法,一点拙见,如有偏颇,望不吝赐教,盼即赐复。
文章中心思想Hybrid Beamforming(简称 HBF )的优点是能够以相较于传统Full Digital beamforming(简称FD)更低的功耗和硬件成本实现接近FD的性能。在目前的半导体技术下,HBF更有利于应用到实际的大规模MIMO系统中。本文为了求解最优HBF,提出了一种坐标迭代下降算法,即:通过更新HBF中Analog beamforming的每个元素而达到最佳性能。
全文概览 系统模型 考虑一个窄带下行单小区多用户分布式天线系统,具体配置如下:基站端有
N
N
N根天线,
N
t
R
F
N_{t}^{\mathrm{RF}}
NtRF条发送射频链,
K
K
K个服务用户,每个用户配有
M
M
M根天线,
N
r
R
F
N_{r}^{\mathrm{RF}}
NrRF条接收射频链。每个用户所需的数据流数目为
d
d
d,并且满足
K
d
≤
N
t
R
F
≤
N
K d \leq N_{t}^{\mathrm{RF}} \leq N
Kd≤NtRF≤N,
d
≤
N
r
R
F
≤
M
d \leq N_{r}^{\mathrm{RF}} \leq M
d≤NrRF≤M和
N
s
=
K
d
N_{s}=K d
Ns=Kd。在混合波束赋形架构中,基站首先在基带使用一个
N
t
R
F
×
N
s
N_{t}^{R F} \times N_{s}
NtRF×Ns的digital precoder
V
D
\mathbf{V}_{D}
VD进行数字波束赋形,然后通过
N
t
R
F
N_{t}^{R F}
NtRF条发送射频链上变频到载频。随后使用一个通过模拟移相器实现大小为
N
×
N
t
R
F
N \times N_{t}^{R F}
N×NtRF的RF precoder
V
R
F
\mathbf{V}_{RF}
VRF(受到恒模约束:
∣
V
R
F
(
i
,
j
)
∣
2
=
1
\left|\mathbf{V}_{R F}(i, j)\right|^{2}=1
∣VRF(i,j)∣2=1)构造最终的发射信号。发射信号可以表示为:
x
=
V
R
F
V
D
s
=
∑
l
=
1
K
V
R
F
V
D
i
s
l
\mathbf{x}=\mathbf{V}_{R F} \mathbf{V}_{D} \mathbf{s}=\sum_{l=1}^{K} \mathbf{V}_{R F} \mathbf{V}_{D_{i}} \mathbf{s}_{l}
x=VRFVDs=l=1∑KVRFVDisl
考虑一个窄带下行单小区多用户分布式天线系统,具体配置如下:基站端有
N
N
N根天线,
N
t
R
F
N_{t}^{\mathrm{RF}}
NtRF条发送射频链,
K
K
K个服务用户,每个用户配有
M
M
M根天线,
N
r
R
F
N_{r}^{\mathrm{RF}}
NrRF条接收射频链。每个用户所需的数据流数目为
d
d
d,并且满足
K
d
≤
N
t
R
F
≤
N
K d \leq N_{t}^{\mathrm{RF}} \leq N
Kd≤NtRF≤N,
d
≤
N
r
R
F
≤
M
d \leq N_{r}^{\mathrm{RF}} \leq M
d≤NrRF≤M和
N
s
=
K
d
N_{s}=K d
Ns=Kd。在混合波束赋形架构中,基站首先在基带使用一个
N
t
R
F
×
N
s
N_{t}^{R F} \times N_{s}
NtRF×Ns的digital precoder
V
D
\mathbf{V}_{D}
VD进行数字波束赋形,然后通过
N
t
R
F
N_{t}^{R F}
NtRF条发送射频链上变频到载频。随后使用一个通过模拟移相器实现大小为
N
×
N
t
R
F
N \times N_{t}^{R F}
N×NtRF的RF precoder
V
R
F
\mathbf{V}_{RF}
VRF(受到恒模约束:
∣
V
R
F
(
i
,
j
)
∣
2
=
1
\left|\mathbf{V}_{R F}(i, j)\right|^{2}=1
∣VRF(i,j)∣2=1)构造最终的发射信号。发射信号可以表示为:
x
=
V
R
F
V
D
s
=
∑
l
=
1
K
V
R
F
V
D
i
s
l
\mathbf{x}=\mathbf{V}_{R F} \mathbf{V}_{D} \mathbf{s}=\sum_{l=1}^{K} \mathbf{V}_{R F} \mathbf{V}_{D_{i}} \mathbf{s}_{l}
x=VRFVDs=l=1∑KVRFVDisl
其中 V D = ⌊ V D 1 , V D 2 , … , V D K ⌋ \mathbf{V}_{D}=\left\lfloor\mathbf{V}_{D_{1}}, \mathbf{V}_{D_{2}}, \ldots, \mathbf{V}_{D_{K}}\right\rfloor VD=⌊VD1,VD2,…,VDK⌋, s ∈ C N s × 1 \mathbf{s} \in \mathbf{C}^{N_{s} \times 1} s∈CNs×1,其包含了 K K K个用户的数据流。对于第 k k k用户,接收信号可以建模为:
y k = H k V R F V D k s k + H k ∑ l ≠ k V R F V D l s l + z k \mathbf{y}_{k}=\mathbf{H}_{k} \mathbf{V}_{R F} \mathbf{V}_{D_{k}} \mathbf{s}_{k}+\mathbf{H}_{k} \sum_{l \neq k} \mathbf{V}_{R F} \mathbf{V}_{D_{l}} \mathbf{s}_{l}+\mathbf{z}_{k} yk=HkVRFVDksk+Hkl=k∑VRFVDlsl+zk
其中: H k ∈ C M × N \mathbf{H}_{k} \in \mathbf{C}^{M \times N} Hk∈CM×N,它是基站发射天线到第 k k k个用户天线的复信道增益矩阵, z k ∼ C N ( 0 , σ 2 I M ) \mathbf{z}_{k} \sim \mathcal{C} N\left(0, \sigma^{2} \mathbf{I}_{M}\right) zk∼CN(0,σ2IM)代表高斯加性白噪声。
在接收端,对于用户 k k k首先使用一个大小为 M × N t R F M \times N_{t}^{R F} M×NtRF的RF combiner(受到恒模约束: ∣ V R F ( i , j ) ∣ 2 = 1 \left|\mathbf{V}_{R F}(i, j)\right|^{2}=1 ∣VRF(i,j)∣2=1)进行处理,然后通过 N r R F N_{r}^{R F} NrRF条射频链下变频到基带,经过digital combiner W D k ∈ C N r R F × d \mathbf{W}_{D_{k}} \in \mathbf{C}^{N_{r}^{R F} \times d} WDk∈CNrRF×d处理后得到最终的数据流。因此,最终处理的信号可以表示为: y ~ k = W t k H H k V t k s k + W t k H H k ∑ l ≠ k V t l s l + W t k H z k \widetilde{\mathbf{y}}_{k}=\mathbf{W}_{t_{k}}^{H} \mathbf{H}_{k} \mathbf{V}_{t_{k}} \mathbf{s}_{k}+\mathbf{W}_{t_{k}}^{H} \mathbf{H}_{k} \sum_{l \neq k} \mathbf{V}_{t_{l}} \mathbf{s}_{l}+\mathbf{W}_{t_{k}}^{H} \mathbf{z}_{k} y k=WtkHHkVtksk+WtkHHkl=k∑Vtlsl+WtkHzk 其中: V t k = V R F V D k \mathbf{V}_{t_{k}}=\mathbf{V}_{R F} \mathbf{V}_{D_{k}} Vtk=VRFVDk, W t k = W R F k W D k \mathbf{W}_{t_{k}}=\mathbf{W}_{R F_{k}} \mathbf{W}_{D_{k}} Wtk=WRFkWDk。对于这样一个系统,第 k k k个用户在高斯信号假设下的总频谱效率可以表示为: R k = log 2 ∣ I M + W t k C − 1 W t k H H k V t k V t k H H k H ∣ R_{k}=\log _{2}\left|\mathbf{I}_{M}+\mathbf{W}_{t_{k}} \mathbf{C}^{-1} \mathbf{W}_{t_{k}}^{H} \mathbf{H}_{k} \mathbf{V}_{t_{k}} \mathbf{V}_{t_{k}}^{H} \mathbf{H}_{k}^{H}\right| Rk=log2∣∣IM+WtkC−1WtkHHkVtkVtkHHkH∣∣ 其中 C k = W t k H H k ( ∑ l ≠ k V t l V t i H ) H k H W t k + σ 2 W t k H W t k \mathbf{C}_{k}=\mathbf{W}_{t_{k}}^{H} \mathbf{H}_{k}\left(\sum_{l \neq k} \mathbf{V}_{t_{l}} \mathbf{V}_{t_{i}}^{H}\right) \mathbf{H}_{k}^{H} \mathbf{W}_{t_{k}}+\sigma^{2} \mathbf{W}_{t_{k}}^{H} \mathbf{W}_{t_{k}} Ck=WtkHHk(∑l=kVtlVtiH)HkHWtk+σ2WtkHWtk。考虑恒模约束,功率约束,以最大频谱效率为目标函数的HBF设计问题可以描述为:

在该窄带场景下, K = 1 K=1 K=1, min ( N , M ) ≥ N s \min (N, M) \geq N_{s} min(N,M)≥Ns。为了不失一般性, N t R F = N r R F = N R F N_{t}^{R F}=N_{r}^{R F}=N^{R F} NtRF=NrRF=NRF。此时的总频谱效率可以写为: R = log 2 ∣ I M + 1 σ 2 W t ( W t H W t ) − 1 W t H H V t V t H H H ∣ R=\log _{2}\left|\mathbf{I}_{M}+\frac{1}{\sigma^{2}} \mathbf{W}_{t}\left(\mathbf{W}_{t}^{H} \mathbf{W}_{t}\right)^{-1} \mathbf{W}_{t}^{H} \mathbf{H} \mathbf{V}_{t} \mathbf{V}_{t}^{H} \mathbf{H}^{H}\right| R=log2∣∣∣∣IM+σ21Wt(WtHWt)−1WtHHVtVtHHH∣∣∣∣其中 V t = V R F V D \mathbf{V}_{t}=\mathbf{V}_{R F} \mathbf{V}_{D} Vt=VRFVD, W t = W R F W D \mathbf{W}_{t}=\mathbf{W}_{R F} \mathbf{W}_{D} Wt=WRFWD。 作者的思路是:首先假设接收端是最优的,设计最优hybrid precoders。然后针对已经设计好的发送端,在设计最优hybrid combiner。于是,发送端的设计问题可以写为:
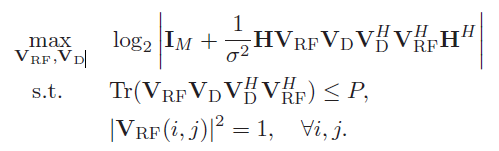
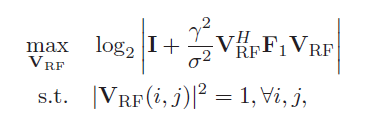

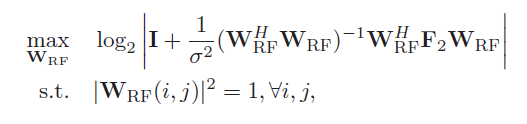
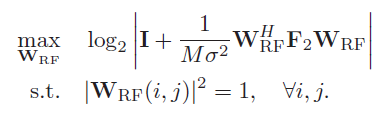
最近更新
- 深拷贝和浅拷贝的区别(重点)
- 【Vue】走进Vue框架世界
- 【云服务器】项目部署—搭建网站—vue电商后台管理系统
- 【React介绍】 一文带你深入React
- 【React】React组件实例的三大属性之state,props,refs(你学废了吗)
- 【脚手架VueCLI】从零开始,创建一个VUE项目
- 【React】深入理解React组件生命周期----图文详解(含代码)
- 【React】DOM的Diffing算法是什么?以及DOM中key的作用----经典面试题
- 【React】1_使用React脚手架创建项目步骤--------详解(含项目结构说明)
- 【React】2_如何使用react脚手架写一个简单的页面?


微信扫码登录

