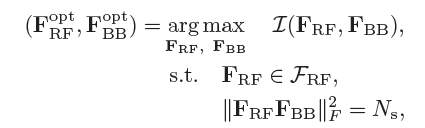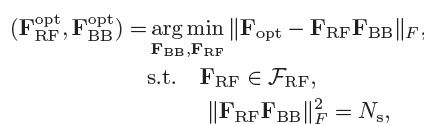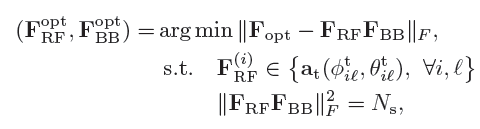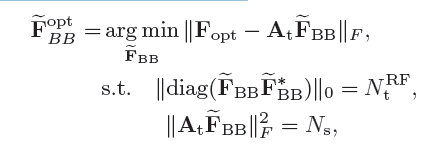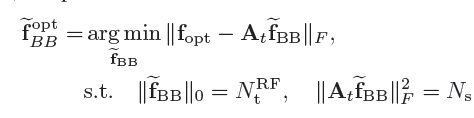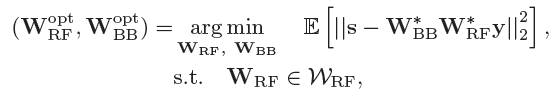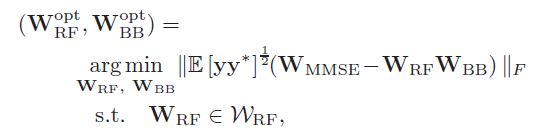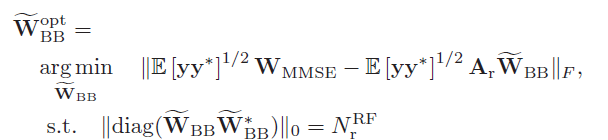混合波束成形| 基于正交匹配追踪（Orthogonal Matching Pursuit）法的混合波束赋形算法

       混合波束赋形专栏|基于正交匹配追踪（Orthogonal Matching Pursuit）法的混合波束赋形算法：整理一篇2014年IEEE TWC高引论文，一点拙见，如有偏颇，望不吝赐教，盼即赐复。

       本文利用mmWava信道的稀疏特性将precoding/combining问题表示为稀疏重构问题，使用基追踪的原理，提出了一种能够逼近最优无约束precoder和combiner的算法，它们能够在低成本射频硬件中实现。

       到目前为止，无线网络的容量已经随着数据流量的增加而扩大，这主要是由于区域频谱效率（bits/s/Hz/m²）的提高。许多物理层的增强如：多天线，信道编码、干扰协调，以及网络致密化的总体趋势都起到了实现这种频谱效率的作用。但在物理层似乎没有什么进一步提高的空间，而且异构网络的广泛部署也不是没有挑战，仅凭这些技术可能不足以满足未来的流量需求。因此，增加商业无线系统可用的频谱，潜在地通过探索新的、不拥挤的频谱带，是一个有希望增加网络容量的解决方案。        例如，毫米波(mmWave)通信在室内无线系统和室外固定系统中实现了每秒千兆比特的数据速率。mmWave硬件的进步和频谱的潜在可用性促使无线行业考虑将mmWave用于室外蜂窝系统的接入链路。但是mmWave的缺点也是十分明显的，随着其频率的增加，在传播过程中的路径损耗十分严重，绕射能力差。但是，毫米波天然的波长优势促使其与大规模天线的结合。大规模天线可以提供克服路径损耗所需的波束赋形增益，可以对多个数据流进行预编码，从而提高频谱效率，使系统接近容量。        无论载波频率如何，预编码的基本原理是相同的，而mmWave系统中的信号处理受到一系列非平凡的实际约束。例如：传统的MIMO处理通常是在基带实现的，它能够控制信号的相位和幅值。然而，数字处理要求为每个天线元件配置专用的基带和射频硬件。遗憾的是，由于mmWave混合信号处理硬件的高成本和高功耗，目前还无法实现这种全数字结构，迫使mmWave系统严重依赖模拟或射频处理。Analog precoding通常使用移相器实现，它对RF precoder施加恒模约束。虽然其实现较为简单，功耗较低，但是它能够提供的阵列增益有限，性能较差。针对这种情况，Hybrid Beamforming(HBF)能够很好的解决这一问题。以发送端为例，它将整个Beamforming分为一个低维度的基带digtial precoder和高维度的analog precoder。这种结构能够大大的减少硬件开销，并且接近Full Digital Beamforming的性能。

       考虑上图所示的单用户mmWave系统，具有 N t N_{\mathrm{t}} Nt​根天线的发射端同具有 N r N_{\mathbf{r}} Nr​根天线的接收端通信 N s N_{\mathrm{s}} Ns​个数据流。为了支持多流通信，发送端配置有 N t R F N_{\mathrm{t}}^{\mathrm{RF}} NtRF​条射频链，且满足： N s ≤ N t R F ≤ N t N_{\mathrm{s}} \leq N_{\mathrm{t}}^{\mathrm{RF}} \leq N_{\mathrm{t}} Ns​≤NtRF​≤Nt​。这种硬件结构使发射机能够使用大小为 N t R F × N s N_{\mathrm{t}}^{\mathrm{RF}} \times N_{\mathrm{s}} NtRF​×Ns​的digital precoder F B B \mathbf{F}_{\mathrm{BB}} FBB​进行数字波束赋形，通过 N t R F N_{\mathrm{t}}^{\mathrm{RF}} NtRF​条射频链上变频后，尾随一个 N t × N t R F N_{\mathrm{t}} \times N_{\mathrm{t}}^{\mathrm{RF}} Nt​×NtRF​的RF precoder F R F \mathbf{F}_{\mathrm{RF}} FRF​进行模拟波束赋形。离散时间发送信号可以表示为： x = F R F F B B S \mathbf{x}=\mathbf{F}_{\mathbf{R} \mathbf{F}} \mathbf{F}_{\mathbf{B} \mathbf{B}} \mathbf{S} x=FRF​FBB​S，其中 S \mathbf{S} S是大小为 N s × 1 N_{\mathrm{s}} \times 1 Ns​×1的符号向量且满足 E [ s s ∗ ] = 1 N s I N s \mathbb{E}\left[\mathbf{s s}^{*}\right]=\frac{1}{N_{\mathbf{s}}} \mathbf{I}_{N_{s}} E[ss∗]=Ns​1​INs​​。由于模拟移相器的使用， F R F \mathbf{F}_{\mathrm{RF}} FRF​受到一个恒模约束，即： ( F R F ( i ) F R F ( i ) ∗ ) ℓ , ℓ = N t − 1 \left(\mathbf{F}_{\mathrm{RF}}^{(i)} \mathbf{F}_{\mathrm{RF}}^{(i) *}\right)_{\ell, \ell}=N_{\mathrm{t}}^{-1} (FRF(i)​FRF(i)∗​)ℓ,ℓ​=Nt−1​， ( ⋅ ) ℓ , ℓ (\cdot)_{\ell, \ell} (⋅)ℓ,ℓ​代表一个矩阵的第 ℓ \ell ℓ个对角线元素。发送端受到一个个总功率约束： ∥ F R F F B B ∥ F 2 = N s \left\|\mathbf{F}_{\mathrm{RF}} \mathbf{F}_{\mathrm{BB}}\right\|_{F}^{2}=N_{\mathrm{s}} ∥FRF​FBB​∥F2​=Ns​。        考虑一个分组衰落传播信道，发送信号可以表示为： y = ρ H F R F F B B s + n \mathbf{y}=\sqrt{\rho} \mathbf{H} \mathbf{F}_{\mathrm{RF}} \mathbf{F}_{\mathrm{BB}} \mathbf{s}+\mathbf{n} y=ρ ​HFRF​FBB​s+n       其中 H \mathbf{H} H是大小为 N r × N t N_{\mathrm{r}} \times N_{\mathrm{t}} Nr​×Nt​的信道向量， ρ \rho ρ代表平均接收功率，加性高斯白噪声服从 C N ( 0 , σ n 2 ) \mathcal{C} \mathcal{N}\left(0, \sigma_{\mathrm{n}}^{2}\right) CN(0,σn2​)分布。接收端通过Hybrid combining的处理，最后的接收信号可以表示为 y ~ = ρ W B B ∗ W R F ∗ H F R F F B B S + W B B ∗ W R F ∗ n \widetilde{\mathbf{y}}=\sqrt{\rho} \mathbf{W}_{\mathrm{BB}}^{*} \mathbf{W}_{\mathrm{RF}}^{*} \mathbf{H F}_{\mathrm{RF}} \mathbf{F}_{\mathrm{BB}} \mathbf{S}+\mathbf{W}_{\mathrm{BB}}^{*} \mathbf{W}_{\mathrm{RF}}^{*} \mathbf{n} y ​=ρ ​WBB∗​WRF∗​HFRF​FBB​S+WBB∗​WRF∗​n        W R F \mathbf{W}_{\mathrm{RF}} WRF​是大小为 N r × N r R F N_{\mathrm{r}} \times N_{\mathrm{r}}^{\mathrm{RF}} Nr​×NrRF​的RF combining矩阵， W B B \mathbf{W}_{\mathrm{BB}} WBB​是大小为 N r R F × N s N_{\mathrm{r}}^{\mathrm{RF}} \times N_{\mathrm{s}} NrRF​×Ns​的基带digital combining矩阵。 W R F \mathbf{W}_{\mathrm{RF}} WRF​同样受到一个 ( W R F ( i ) W R F ( i ) ∗ ) ℓ , ℓ = N r − 1 \left(\mathbf{W}_{\mathrm{RF}}^{(i)} \mathbf{W}_{\mathrm{RF}}^{(i) *}\right)_{\ell, \ell}=N_{\mathrm{r}}^{-1} (WRF(i)​WRF(i)∗​)ℓ,ℓ​=Nr−1​的恒模约束。这样一个在mmWave信道中高斯信号假设下可实现频谱效率可以表示为： R = log ⁡ 2 ( ∣ I N s + ρ N s R n − 1 W B B ∗ W R F ∗ H F R F F B B × F B B ∗ F R F ∗ H ∗ W R F W B B ∣ ) \begin{aligned} R=\log _{2}\left(\left|\mathbf{I}_{N_{\mathrm{s}}}+\frac{\rho}{N_{\mathrm{s}}} \mathbf{R}_{\mathrm{n}}^{-1}\right.\right.& \mathbf{W}_{\mathrm{BB}}^{*} \mathbf{W}_{\mathrm{RF}}^{*} \mathbf{H F}_{\mathrm{RF}} \mathbf{F}_{\mathrm{BB}} \\ \times & \mathbf{F}_{\mathrm{BB}}^{*} \mathbf{F}_{\mathrm{RF}}^{*} \mathbf{H}^{*} \mathbf{W}_{\mathrm{RF}} \mathbf{W}_{\mathrm{BB}} | ) \end{aligned} R=log2​(∣∣∣∣​INs​​+Ns​ρ​Rn−1​×​WBB∗​WRF∗​HFRF​FBB​FBB∗​FRF∗​H∗WRF​WBB​∣)​       其中 R n = σ n 2 W B B ∗ W R F ∗ W R F W B B \mathbf{R}_{\mathrm{n}}=\sigma_{\mathrm{n}}^{2} \mathbf{W}_{\mathrm{BB}}^{*} \mathbf{W}_{\mathrm{RF}}^{*} \mathbf{W}_{\mathrm{RF}} \mathbf{W}_{\mathrm{BB}} Rn​=σn2​WBB∗​WRF∗​WRF​WBB​。信道矩阵 H \mathbf{H} H使用Saleh-Valenzuela模型，其表达式为： H = γ ∑ i , ℓ α i ℓ Λ r ( ϕ i ℓ r , θ i ℓ r ) Λ t ( ϕ i ℓ t , θ i ℓ t ) a r ( ϕ i ℓ r , θ i ℓ r ) a t ( ϕ i ℓ t , θ i ℓ t ) ∗ \mathbf{H}=\gamma \sum_{i, \ell} \alpha_{i \ell} \Lambda_{\mathrm{r}}\left(\phi_{i \ell}^{\mathrm{r}}, \theta_{i \ell}^{\mathrm{r}}\right) \Lambda_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}}, \theta_{i \ell}^{\mathrm{t}}\right) \mathbf{a}_{\mathrm{r}}\left(\phi_{i \ell}^{\mathrm{r}}, \theta_{i \ell}^{\mathrm{r}}\right) \mathbf{a}_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}}, \theta_{i \ell}^{\mathrm{t}}\right)^{*} H=γi,ℓ∑​αiℓ​Λr​(ϕiℓr​,θiℓr​)Λt​(ϕiℓt​,θiℓt​)ar​(ϕiℓr​,θiℓr​)at​(ϕiℓt​,θiℓt​)∗       表达式中的参数介绍请参照论文。

       HBF的设计中需要联合优化四个变量 ( F R F , F B B , W R F , W B B ) \left(\mathbf{F}_{\mathbf{R F}}, \mathbf{F}_{\mathbf{B B}}, \mathbf{W}_{\mathbf{R F}}, \mathbf{W}_{\mathrm{BB}}\right) (FRF​,FBB​,WRF​,WBB​)的问题，直接求解是很困难的，因此本文将HBF问题解耦成接收端HBF设计和发送端HBF设计。因此，在发送端，使用最大化互信息 I ( F R F , F B B ) \mathcal{I}\left(\mathbf{F}_{\mathrm{RF}}, \mathbf{F}_{\mathrm{BB}}\right) I(FRF​,FBB​)代替最大化频谱效率为目标函数，即： I ( F R F , F B B ) = log ⁡ 2 ( ∣ I + ρ N s σ n 2 H F R F F B B F B B ∗ F R F ∗ H ∗ ∣ ) \mathcal{I}\left(\mathbf{F}_{\mathrm{RF}}, \mathbf{F}_{\mathrm{BB}}\right)=\log _{2}\left(\left|\mathbf{I}+\frac{\rho}{N_{\mathrm{s}} \sigma_{\mathrm{n}}^{2}} \mathbf{H F}_{\mathrm{RF}} \mathbf{F}_{\mathrm{BB}} \mathbf{F}_{\mathrm{BB}}^{*} \mathbf{F}_{\mathrm{RF}}^{*} \mathbf{H}^{*}\right|\right) I(FRF​,FBB​)=log2​(∣∣∣∣​I+Ns​σn2​ρ​HFRF​FBB​FBB∗​FRF∗​H∗∣∣∣∣​)        则 F R F F B B \mathbf{F}_{\mathrm{RF}} \mathbf{F}_{\mathrm{BB}} FRF​FBB​的最优precoding问题可以描述为：

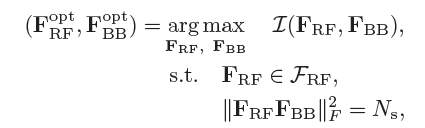
        博主认为该文章的亮点之一是，推导了 I ( F R F , F B B ) \mathcal{I}\left(\mathbf{F}_{\mathrm{RF}}, \mathbf{F}_{\mathrm{BB}}\right) I(FRF​,FBB​)可以近似为 ∥ F o p t − F R F F B B ∥ F \left\|\mathbf{F}_{\mathrm{opt}}-\mathbf{F}_{\mathrm{RF}} \mathbf{F}_{\mathrm{BB}}\right\|_{F} ∥Fopt​−FRF​FBB​∥F​（ 这也作为了后续一些Hybrid precoding的目标函数，推导过程十分精彩，具体可以参照原文。）因此，最优precoding的问题可以表示为:

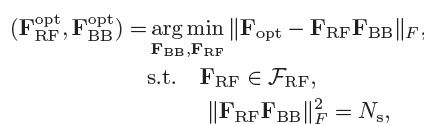
        （ 本 文 重 头 戏 ） \color{red}{（本文重头戏）} （本文重头戏）为了使用OMP的算法，作者利用簇信道模型产生mmWave MIMO信道的结构，即以下四点性质：        1.Optimal precoder的结构： F o p t = V 1 \mathbf{F}_{\mathrm{opt}}=\mathbf{V}_{1} Fopt​=V1​,（ V \mathbf{V} V是信道 H \mathbf{H} H的SVD分解，且 V = [ V 1 V 2 ] \mathbf{V}=\left[ \begin{array}{ll}{\mathbf{V}_{1}} & {\mathbf{V}_{2}}\end{array}\right] V=[V1​​V2​​]），酉矩阵 V \mathrm{V} V的列构成信道行空间的一组标准正交基。        2.簇mmWave信道的结构：当 N c l N r a y ≤ N t N_{\mathrm{cl}} N_{\mathrm{ray}} \leq N_{\mathrm{t}} Ncl​Nray​≤Nt​时，阵列响应 a t ( ϕ i ℓ t , θ i ℓ t ) \mathbf{a}_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}}, \theta_{i \ell}^{\mathrm{t}}\right) at​(ϕiℓt​,θiℓt​)线性无关，因此 a t ( ϕ i ℓ t , θ i ℓ t ) \mathbf{a}_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}}, \theta_{i \ell}^{\mathrm{t}}\right) at​(ϕiℓt​,θiℓt​)可以组成信道行空间的另一组最小基（ N c l N r a y ≤ min ⁡ ( N t , N r ) N_{\mathrm{cl}} N_{\mathrm{ray}} \leq \min \left(N_{\mathrm{t}}, N_{\mathrm{r}}\right) Ncl​Nray​≤min(Nt​,Nr​)）。        3. F o p t \mathbf{F}_{\mathrm{opt}} Fopt​和 a t ( ϕ i ℓ t θ i ℓ t ) \mathbf{a}_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}} \theta_{i \ell}^{\mathrm{t}}\right) at​(ϕiℓt​θiℓt​)的联系： F  opt  \mathbf{F}_{\text { opt }} F opt ​可以表示为 a t ( ϕ i ℓ t , θ i ℓ t ) , ∀ i , ℓ \mathbf{a}_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}}, \theta_{i \ell}^{\mathrm{t}}\right), \forall i, \ell at​(ϕiℓt​,θiℓt​),∀i,ℓ的线性组合。        4.向量 a t ( ϕ i ℓ t θ i ℓ t ) \mathbf{a}_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}} \theta_{i \ell}^{\mathrm{t}}\right) at​(ϕiℓt​θiℓt​)可以作为 F R F \mathbf{F}_{\mathrm{RF}} FRF​的列：向量 a t ( ϕ i ℓ t θ i ℓ t ) \mathbf{a}_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}} \theta_{i \ell}^{\mathrm{t}}\right) at​(ϕiℓt​θiℓt​)是恒模、仅相位变化的向量。因此，mmWave发射端可以在RF上（通过RF precoder F R F \mathbf{F}_{\mathrm{RF}} FRF​）使用 N t R F N_{\mathrm{t}}^{\mathrm{RF}} NtRF​个 a t ( ϕ i ℓ t , θ i ℓ t ) \mathbf{a}_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}}, \theta_{i \ell}^{\mathrm{t}}\right) at​(ϕiℓt​,θiℓt​)向量，通过它的 F B B \mathbf{F}_{\mathrm{BB}} FBB​形成任意线性组合。也就是说，我们能够构造一个线性组合，使得 ∥ F o p t − F R F F B B ∥ F \left\|\mathbf{F}_{\mathrm{opt}}-\mathbf{F}_{\mathrm{RF}} \mathbf{F}_{\mathrm{BB}}\right\|_{F} ∥Fopt​−FRF​FBB​∥F​最小。        利用上面的四点性质，近似最优hybrid precoders的设计问题可以表示为：

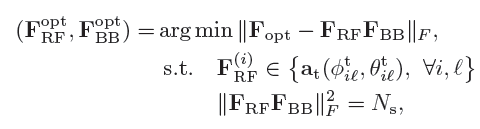
       这相当于使用基向量 a t ( ϕ i ℓ t , θ i , ℓ t ) \mathbf{a}_{\mathrm{t}}\left(\phi_{i \ell}^{\mathrm{t}}, \theta_{i, \ell}^{\mathrm{t}}\right) at​(ϕiℓt​,θi,ℓt​)找出 F o p t \mathbf{F}_{\mathrm{opt}} Fopt​最优低维表示。利用上述的4个性质，precoding问题由选择“best” N t R F N_{\mathrm{t}}^{\mathrm{RF}} NtRF​个阵列响应向量和找出最佳基带组合（也就是 F B B \mathbf{F}_{\mathrm{BB}} FBB​）， F R F ( i ) \mathbf{F}_{\mathrm{RF}}^{(i)} FRF(i)​的约束可以直接嵌入到优化目标中以得到如下的等价问题：

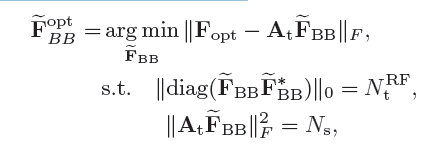
       其中 A t = [ a t ( ϕ 1 , 1 t , θ 1 , 1 t ) , … , a t ( ϕ N c l , N r a v t θ N c l , N r a y t ) ] \mathbf{A}_{\mathrm{t}}=\left[\mathrm{a}_{\mathrm{t}}\left(\phi_{1,1}^{\mathrm{t}}, \theta_{1,1}^{\mathrm{t}}\right), \ldots, \mathrm{a}_{\mathrm{t}}\left(\phi_{N_{\mathrm{cl}}, N_{\mathrm{rav}}}^{\mathrm{t}} \theta_{N_{\mathrm{cl}}, N_{\mathrm{ray}}}^{\mathrm{t}}\right)\right] At​=[at​(ϕ1,1t​,θ1,1t​),…,at​(ϕNcl​,Nrav​t​θNcl​,Nray​t​)]是一个大小为 N t × N c l N r a y N_{\mathrm{t}} \times N_{\mathrm{cl}} N_{\mathrm{ray}} Nt​×Ncl​Nray​的阵列响应向量矩阵， F ~ B B \widetilde{\mathbf{F}}_{\mathrm{BB}} F BB​是一个大小为 N c l N r a y × N s N_{\mathrm{cl}} N_{\mathrm{ray}} \times N_{\mathrm{s}} Ncl​Nray​×Ns​的矩阵。 A t \mathbf{A}_{\mathrm{t}} At​和 F ~ B B \widetilde{\mathbf{F}}_{\mathrm{BB}} F BB​可以视为一个辅助矩阵，从中我们可以分别获得 F R F o p t \mathbf{F}_{\mathrm{RF}}^{\mathrm{opt}} FRFopt​和 F B B o p t \mathbf{F}_{\mathrm{BB}}^{\mathrm{opt}} FBBopt​。更进一步的解释：稀疏约束 ∥ diag ⁡ ( F ~ B B F ~ B B ∗ ) ∥ 0 = N t R F \left\|\operatorname{diag}\left(\widetilde{\mathbf{F}}_{\mathrm{BB}} \widetilde{\mathbf{F}}_{\mathrm{BB}}^{*}\right)\right\|_{0}=N_{\mathrm{t}}^{\mathrm{RF}} ∥∥∥​diag(F BB​F BB∗​)∥∥∥​0​=NtRF​表示 F ~ B B \widetilde{\mathbf{F}}_{\mathrm{BB}} F BB​不能有超过 N t R F N_{\mathrm{t}}^{\mathrm{RF}} NtRF​的非0行，这也就意味着，仅当 F ~ B B \widetilde{\mathbf{F}}_{\mathrm{BB}} F BB​的 N t R F N_{\mathrm{t}}^{\mathrm{RF}} NtRF​行非0时， A t \mathbf{A}_{\mathrm{t}} At​的 N t R F N_{\mathrm{t}}^{\mathrm{RF}} NtRF​列被有效选择。因此，基带digitial precoder F B B o p t \mathbf{F}_{\mathrm{BB}}^{\mathrm{opt}} FBBopt​由 F ~ B B o p t \widetilde{\mathbf{F}}_{\mathrm{BB}}^{\mathrm{opt}} F BBopt​的非零行给出，RF precoder F R F o p t \mathbf{F}_{\mathrm{RF}}^{\mathrm{opt}} FRFopt​由 A t \boldsymbol{A}_{\mathrm{t}} At​与之相关的 N t R F N_{\mathrm{t}}^{\mathrm{RF}} NtRF​列给出。         博主认为该文章的亮点之二是：文章将上述联合设计 F R F \mathbf{F}_{\mathrm{RF}} FRF​和 F B B \mathbf{F}_{\mathrm{BB}} FBB​的问题精彩地转化为了一个单变量稀疏约束矩阵重构问题（个人认为是开山之作的地位）。尽管潜在的动机不同，甚至上面问题中所定义的变量看起来也不是这么友好（至少博主第一次读这篇论文的时候觉得怪怪的…很难理解），但所得到的问题的数学表达形式与稀疏信号恢复相关文献中遇到的优化问题相同。因此，有关稀疏重建的大量文献现在可以用于混合预编码设计 （ 这 也 就 是 为 什 么 O M P 方 法 能 够 精 彩 地 应 用 到 H B F 设 计 中 ） \color{red}{（这也就是为什么OMP方法能够精彩地应用到HBF设计中）} （这也就是为什么OMP方法能够精彩地应用到HBF设计中）。当然，为了让上述问题的数学表达形式看起来更加直观一点，可以考虑 F  opt  \mathbf{F}_{\text { opt }} F opt ​是一个列向量的情况，此时的数学问题表达形式就是：

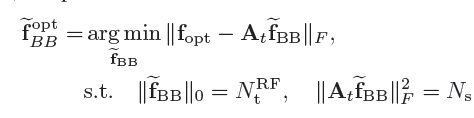
       再去参照任何一本讲解著名算法OMP的书籍就可以更直观地理解这种表达形式（具体可以参照《矩阵分析与应用》（第2版）张贤达著）。综上所述，基于OMP的空间稀疏预编码算法可以表示为：

       博主认为该文章的亮点之三是：OMP的方法不光是能够在precoding的时候使用，在combining的时候同样可以使用。在接收端本文考虑的是最小均方误差（mean-squared-error，MSE）。因此，combiner的设计问题可以表示为：

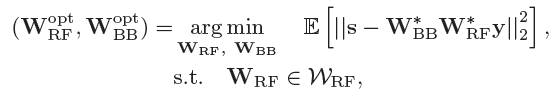
       在无任何硬件约束的条件下，最小均方误差combiner可以求得闭式解：

       首先相目标函数展开，去除掉与 W R F \mathbf{W}_{\mathrm{RF}} WRF​和 W B B \mathbf{W}_{\mathrm{BB}} WBB​无关的项，然后加入与 W R F \mathbf{W}_{\mathrm{RF}} WRF​和 W B B \mathbf{W}_{\mathrm{BB}} WBB​无关的项: tr ⁡ ( W M M S E ∗ E [ y y ∗ ] W M M S E ) − tr ⁡ ( E [ s s ∗ ] ) \operatorname{tr}\left(\mathbf{W}_{\mathrm{MMSE}}^{*} \mathbb{E}\left[\mathbf{y y}^{*}\right] \mathbf{W}_{\mathrm{MMSE}}\right)-\operatorname{tr}\left(\mathbb{E}\left[\mathbf{s s}^{*}\right]\right) tr(WMMSE∗​E[yy∗]WMMSE​)−tr(E[ss∗])，最后巧妙地得到了一个精彩的目标函数等价表达式（具体推导参照论文）： J ( W R F , W B B ) = ∥ E [ y y ∗ ] 1 / 2 ( W M M S E − W R F W B B ) ∥ F 2 \mathcal{J}\left(\mathbf{W}_{\mathbf{R F}}, \mathbf{W}_{\mathrm{BB}}\right)=\left\|\mathbb{E}\left[\mathrm{yy}^{*}\right]^{1 / 2}\left(\mathrm{W}_{\mathrm{MMSE}}-\mathbf{W}_{\mathrm{RF}} \mathbf{W}_{\mathrm{BB}}\right)\right\|_{F}^{2} J(WRF​,WBB​)=∥∥∥​E[yy∗]1/2(WMMSE​−WRF​WBB​)∥∥∥​F2​        因此，原combiner优化问题可以重新表示为：

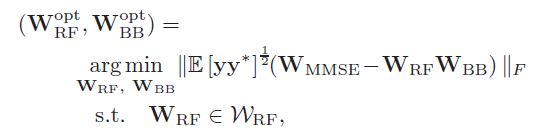
       可以看出：这与发送端precoder的稀疏重构问题十分十分地相似，因此，这也就是为什么发送端的OMP算法能够应用到接收端的combiner设计。接收端combiner的稀疏重构问题可以表示为如下：

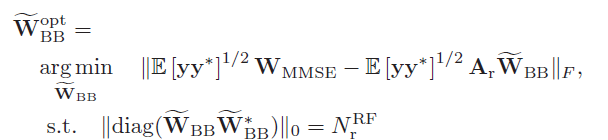
       其中 A r = [ a r ( ϕ 1 , 1 r , θ 1 , 1 r ) , … , a t ( ϕ N c l , N r a v r , θ N c l , N r a y r ) ] \mathbf{A}_{\mathrm{r}}=\left[\mathbf{a}_{\mathrm{r}}\left(\phi_{1,1}^{\mathrm{r}}, \theta_{1,1}^{\mathrm{r}}\right), \ldots, \mathrm{a}_{\mathrm{t}}\left(\phi_{N_{\mathrm{cl}}, N_{\mathrm{rav}}}^{\mathrm{r}}, \theta_{N_{\mathrm{cl}}, N_{\mathrm{ray}}}^{\mathrm{r}}\right)\right] Ar​=[ar​(ϕ1,1r​,θ1,1r​),…,at​(ϕNcl​,Nrav​r​,θNcl​,Nray​r​)]是大小为 N r × N c l N r a y N_{\mathrm{r}} \times N_{\mathrm{cl}} N_{\mathrm{ray}} Nr​×Ncl​Nray​的阵列响应向量矩阵。 A r A_{\mathrm{r}} Ar​和 W ~ B B \widetilde{\mathbf{W}}_{\mathrm{BB}} W BB​的定义可以结合论文参照上面precoder中的讲解。综上，combiner的设计算法伪代码为：

       对于不同 N t R F N_{\mathrm{t}}^{\mathrm{RF}} NtRF​和 N r R F N_{\mathrm{r}}^{\mathrm{RF}} NrRF​的关系，作者给了两种策略去设计，即：

论文中还有一小节是介绍有限反馈下的空间稀疏预编码，感兴趣的读者可以自行去阅读，但是文章的精华部分已经在上面的介绍中给出。

       仿真的具体参数可以参照文章，博文不再赘述。

注意：有限反馈下的仿真图并未贴上，具体分析，参照论文。

• 专栏： 混合波束成形
• 专栏： 智能反射面
• 混合波束成形|基础：深入浅出5G，毫米波，大规模MIMO与波束赋形
• 混合波束成形|进阶：深入浅出混合波束赋形
• 混合波束成形| 基于坐标迭代更新法的混合波束赋形算法
• 混合波束成形| 基于正交匹配追踪（Orthogonal Matching Pursuit）法的混合波束赋形算法
• 混合波束成形| 论文：基于MMSE准则的混合波束成形算法
• 混合波束成形| 通过天线空间方向图理解波束成形的物理意义
• 混合波束成形| 基于深度学习的大规模天线阵列混合波束成形设计
• 混合波束成形| MIMO系统的DFT码本
• 混合波束成形| HBF系统的克拉美罗下界