本文地址：https://arxiv.org/pdf/1702.00832.pdf GitHub地址：https://github.com/musicbeer/Deep-Learning-for-the-Physical-Layer
- 前言
- 文章主要贡献
- 全文概述
- siso
- mimo
- RTN的引入
深度通信网络专栏|自编码器:这一专栏原计划整理18-19年的论文，这篇虽然是17年的论文，但是首次提出自编码器的概念。现在回看内容比较简单易懂，但因为其引用量很高，其中提出的自编码器的概念和将专家领域知识与NN结合RTN网络结构被多篇文章引用，因此在这里也做个“读书笔记”，方便日后回看。这里仅记录论文中与自编码器相关的部分。
文章主要贡献提出将通信系统理解为自编码器 ，在单进程中联合优化发送接收端 ，将这一思路拓展到MIMO系统，并提出RTNs（radio transformer networks）的概念，将ML模型与专家领域知识结合。
全文概述 siso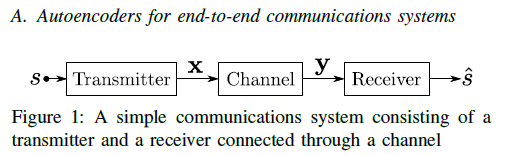
处理过程： (1) 发送机：将信号s（kbits）编码成具有更高传输鲁棒性的表达式X（n维向量）并发送 (2) 信道：AWGN干扰x，输出y (3) 接收机：根据接收y译码出M种可能信号的概率，根据最大概率重构信号 
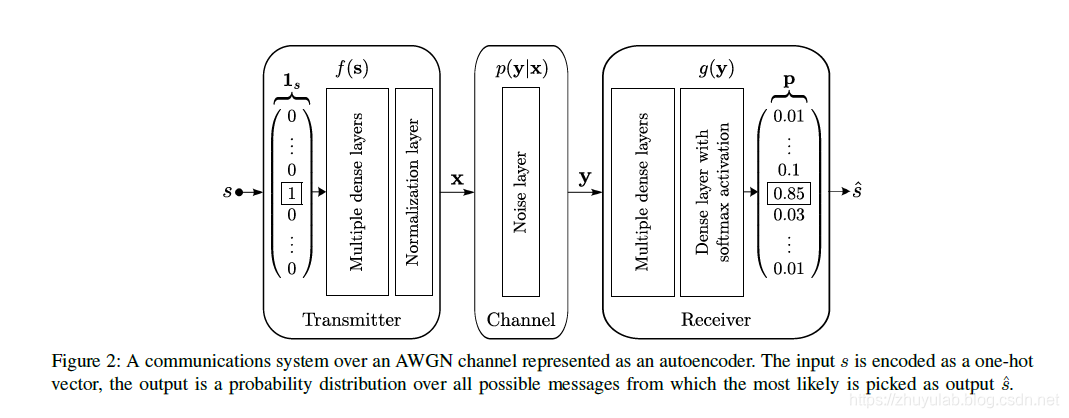神经网络结构如上，输入s为onehot编码，信道为方差固定的高斯信道，在snr=7db时训练，损失函数使用交叉熵，发送NN的归一化层保证x满足功率约束，接收端NN输出概率。网络参数设置如下： 
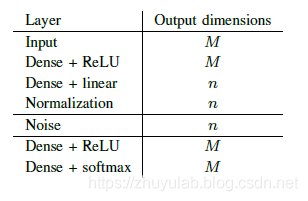snr-ber如下：autoencoder（8，8）的性能优于uncoded bpsk（8，8），说明NN学习到了联合编码调制方案，实现了编码增益。
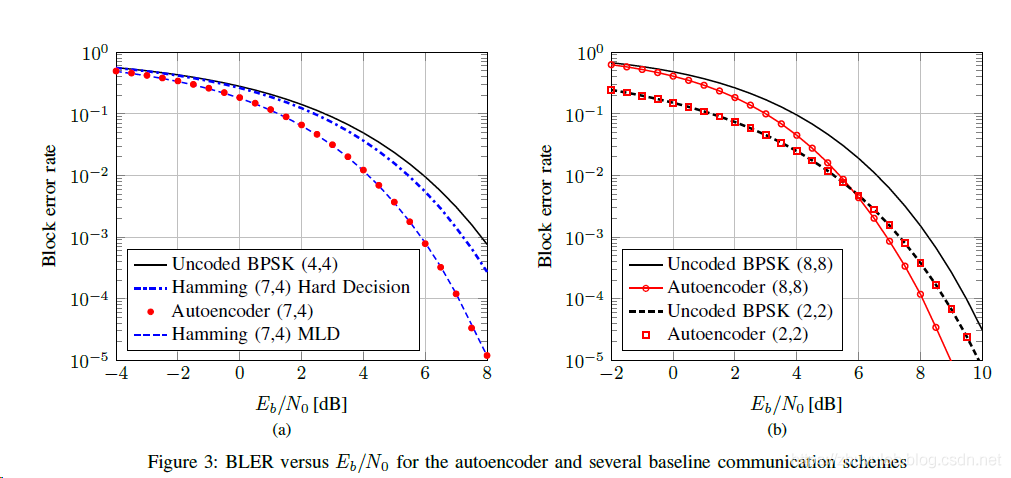编码结果如下：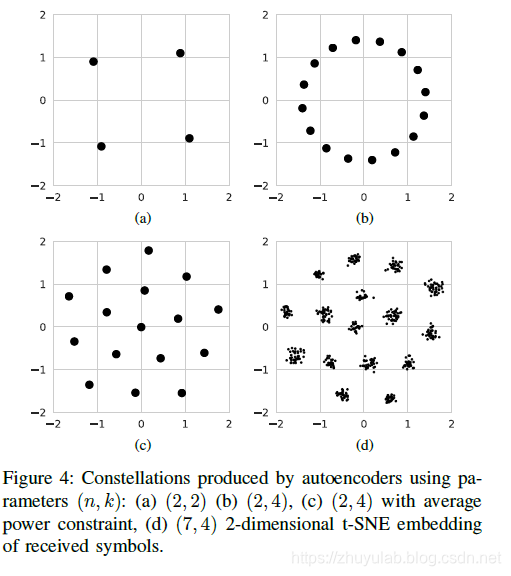 
考虑2发2收的情况：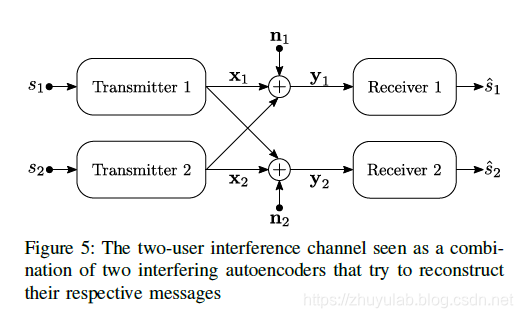 
与siso情况相比，信道引进了干扰
神经网络实现的过程为： 发送NN1将s1编码为x1，发送NN2将s2编码为x2 将x1+x2+n1输入接收NN1，得到估计的s1 将x1+x2+n2输入接收NN2，得到估计的s2
NN1和NN2采用与siso一样的层数及神经元设置 两个自编码器分别优化， 损失函数设置为 L ~ = α L ~ 1 + ( 1 − α ) L ~ 2 \tilde{L}=\alpha \tilde{L}_{1}+(1-\alpha) \tilde{L}_{2} L~=αL~1+(1−α)L~2，其中α可变， α t + 1 = L ~ 1 ( θ t ) L ~ 1 ( θ t ) + L ~ 2 ( θ t ) , t > 0 \alpha_{t+1}=\frac{\tilde{L}_{1}\left(\boldsymbol{\theta}_{t}\right)}{\tilde{L}_{1}\left(\boldsymbol{\theta}_{t}\right)+\tilde{L}_{2}\left(\boldsymbol{\theta}_{t}\right)}, \quad t>0 αt+1=L~1(θt)+L~2(θt)L~1(θt),t>0
ber-snr曲线如下：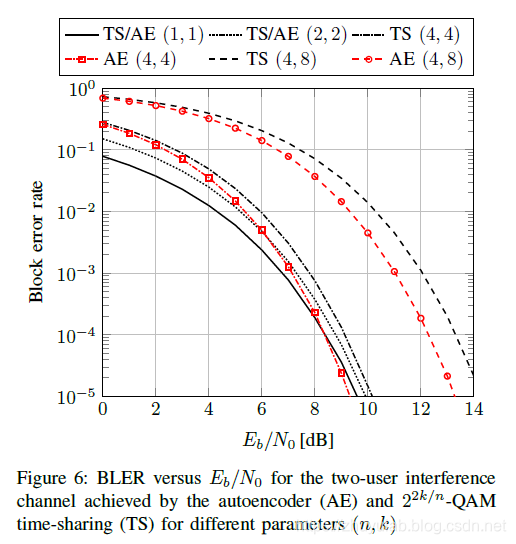 
对比参考曲线为 2 2 k / n − Q A M 2^{2 k / n}-\mathrm{Q} \mathrm{AM} 22k/n−QAM+ time-sharing
星座图如下：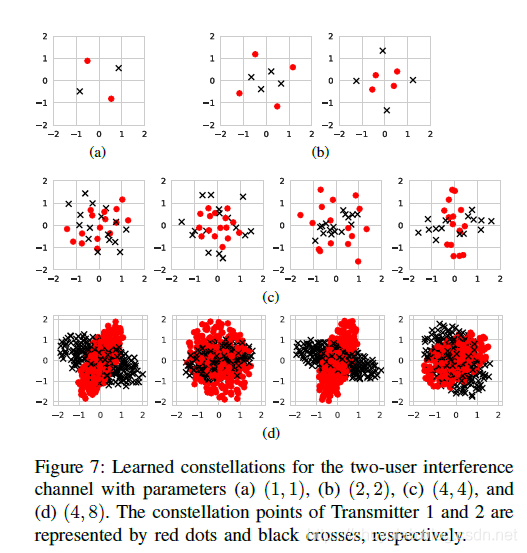 
( a)性能与bpsk相等 ( b)性能与4qam相等 ( c)性能比4qam好0.7db ( d)性能比16qam好1db
因为对比曲线的选取原因，这样的结果也在情理之中，当采用（4，4）或（4，8）时，对比曲线相当于使用了重复编码，这一的方式并不能充分利用自由度，因此神经网络能达到更好的性能。
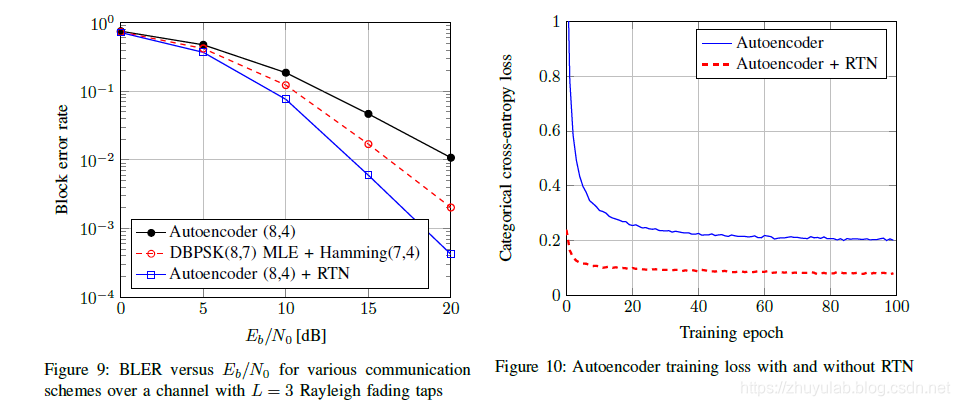
RTN的引入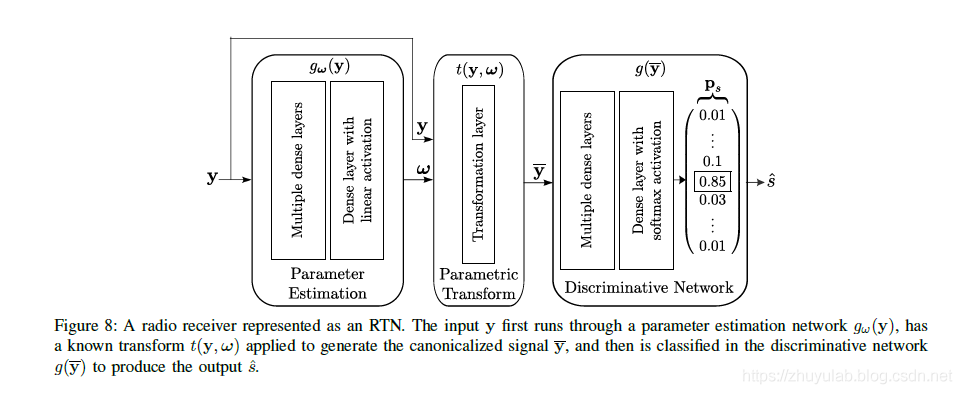
用以上结构代替之前的接收机结构，先将y输入参数估计网络，估计出有用参数（如频偏、符号时间、脉冲响应等），再利用这些NN估计出来的参数对接收信号进行校正，最后输入判别网络。这一结构很好地将NN与传统的已知算法结合，实现了神经网络与专家领域知识的融合，实现了更低的ber，加快了训练速度。 仿真结果： 
