关于 《Channel Estimation for Hybrid Architecture-Based Wideband Millimeter Wave System》一文的中文笔记。
简介 问题背景本文主要讲述了几种基于码本的信道估计方式，难能可贵地考虑了宽带的情况——大部分的相关工作考虑的是窄带系统，然而宽带系统更符合毫米波的实际情况。因此，本文值得一读。
系统结构
这个HBF的结构图和之前一样，不清楚的读者可以去看前几篇博文，这里就不再赘述了。 基于此结构，我们可以推导接收端最终的信号为：
y
[
n
]
=
ρ
∑
d
=
0
N
c
−
1
W
∗
H
d
F
s
[
n
−
d
]
+
W
∗
v
[
n
]
\mathbf{y}[n]=\sqrt{\rho} \sum_{d=0}^{N_{c}-1} \mathbf{W}^{*} \mathbf{H}_{d} \mathbf{F} \mathbf{s}[n-d]+\mathbf{W}^{*} \mathbf{v}[n]
y[n]=ρ
d=0∑Nc−1W∗HdFs[n−d]+W∗v[n]
W
\mathbf{W}
W和
F
\mathbf{F}
F分别是发送端和接收端的波束成形矩阵。 其中，
H
d
\mathbf{H}_d
Hd是：
H
d
=
∑
ℓ
=
1
N
p
α
ℓ
p
(
d
T
s
−
τ
ℓ
)
a
R
(
ϕ
ℓ
)
a
T
∗
(
θ
ℓ
)
\mathbf{H}_{d}=\sum_{\ell=1}^{N_{\mathrm{p}}} \alpha_{\ell} p\left(d T_{\mathrm{s}}-\tau_{\ell}\right) \mathbf{a}_{\mathrm{R}}\left(\phi_{\ell}\right) \mathbf{a}_{\mathrm{T}}^{*}\left(\theta_{\ell}\right)
Hd=ℓ=1∑Npαℓp(dTs−τℓ)aR(ϕℓ)aT∗(θℓ) 这个要详细说明一下，首先，
N
c
N_c
Nc代表的是时延扩展的总长度，也就是说延时最大的那条件的时延是
N
c
N_c
Nc。
H
d
\mathbf{H}_\mathrm{d}
Hd代表的则是延时为
d
T
s
dT_s
dTs的信道（
T
s
T_s
Ts代表一个符号周期），需要注意的是由于只有有限的多径数，所以大部分的
H
d
\mathbf{H}_\mathrm{d}
Hd是没有值的。这一点是通过
p
(
d
T
s
−
τ
ℓ
)
p\left(d T_{\mathrm{s}}-\tau_{\ell}\right)
p(dTs−τℓ)来体现的。
p
(
τ
)
p(\tau)
p(τ)代表的是脉冲成型在
τ
\tau
τ处的响应，可以简单理解为只有
p
(
0
)
=
1
p(0)=1
p(0)=1,在其余点全为0。(实际中可能会用根升余弦滤波器啥的来近似代替，但我们现在暂时以这样理解）。那么，只有当
d
T
s
=
τ
d T_{\mathrm{s}}=\tau
dTs=τ时，该
H
d
\mathbf{H}_\mathrm{d}
Hd才有值，也就是延时刚好为
d
T
s
d T_{\mathrm{s}}
dTs的那条径的值。
a
R
(
ϕ
ℓ
)
a
T
∗
\mathbf{a}_{\mathrm{R}}\left(\phi_{\ell}\right) \mathbf{a}_{\mathrm{T}}^{*}
aR(ϕℓ)aT∗这一项就是基本的ULA天线阵列的响应公式，在此也不再赘述。 于是，
H
d
\mathbf{H}_\mathrm{d}
Hd可表示为：
H
d
=
A
R
Δ
d
A
T
∗
\mathbf{H}_{d}=\mathbf{A}_{\mathrm{R}} \Delta_{d} \mathbf{A}_{\mathrm{T}}^{*}
Hd=ARΔdAT∗ 其中
Δ
d
\Delta_{d}
Δd代表了一个对角阵，对角元素为
α
ℓ
p
(
d
T
S
−
τ
ℓ
)
\alpha_{\ell} p\left(d T_{\mathrm{S}}-\tau_{\ell}\right)
αℓp(dTS−τℓ)。进一步地，通过矩阵列化公式，有
vec
(
H
d
)
=
(
A
‾
T
∘
A
R
)
[
α
1
p
(
d
T
s
−
τ
1
)
α
2
p
(
d
T
s
−
τ
2
)
⋮
α
N
p
p
(
d
T
s
−
τ
N
p
)
]
\operatorname{vec}\left(\mathbf{H}_{d}\right)=\left(\overline{\mathbf{A}}_{\mathrm{T}} \circ \mathbf{A}_{\mathrm{R}}\right)\left[\begin{array}{c}{\alpha_{1} p\left(d T_{\mathrm{s}}-\tau_{1}\right)} \\ {\alpha_{2} p\left(d T_{\mathrm{s}}-\tau_{2}\right)} \\ {\vdots} \\ {\alpha_{N_{\mathrm{p}}} p\left(d T_{\mathrm{s}}-\tau_{N_{\mathrm{p}}}\right)}\end{array}\right]
vec(Hd)=(AT∘AR)⎣⎢⎢⎢⎡α1p(dTs−τ1)α2p(dTs−τ2)⋮αNpp(dTs−τNp)⎦⎥⎥⎥⎤
首先，本文使用的方法中只用模拟阵来估计，默认数字阵为单位阵，不做任何操作，即有：
r
m
[
n
]
=
∑
d
=
0
N
c
−
1
H
d
F
m
s
m
[
n
−
d
]
+
v
m
[
n
]
\mathbf{r}_{m}[n]=\sum_{d=0}^{N_{c}-1} \mathbf{H}_{d} \mathbf{F}_{m} \mathbf{s}_{m}[n-d]+\mathbf{v}_{m}[n]
rm[n]=d=0∑Nc−1HdFmsm[n−d]+vm[n] 其中
F
m
∈
C
N
t
×
N
R
F
\mathbf{F}_{m} \in \mathbb{C}^{N_{t} \times N_{\mathrm{RF}}}
Fm∈CNt×NRF，
s
m
[
n
]
∈
C
N
R
F
×
1
\mathbf{s}_{m}[n] \in \mathbb{C}^{N_{\mathrm{RF}} \times 1}
sm[n]∈CNRF×1为第
m
m
m个训练序列。
s
m
=
[
0
⋯
0
⏟
N
c
−
1
s
m
[
1
]
⋯
s
m
[
N
]
]
\mathbf{s}_{m}=\left[\underbrace{0 \cdots 0}_{N_{\mathrm{c}}-1} \mathbf{s}_{m}[1] \cdots \mathbf{s}_{m}[N]\right]
sm=⎣⎡Nc−1
0⋯0sm[1]⋯sm[N]⎦⎤ 前
N
c
N_c
Nc个为零前缀（ZP），用于防止相邻帧之间的干扰。 如此，可以把N个符号周期内接收到的符号表示为：
y
m
=
[
y
m
[
1
]
y
m
[
2
]
⋮
y
m
[
N
]
]
=
S
m
(
I
N
c
⊗
F
m
T
)
⊗
W
m
∗
h
c
+
e
m
⏟
\mathbf{y}_{m}=\left[\begin{array}{c}{\mathbf{y}_{m}[1]} \\ {\mathbf{y}_{m}[2]} \\ {\vdots} \\ {\mathbf{y}_{m}[N]}\end{array}\right]=\underbrace{\mathbf{S}_{m}\left(\mathbf{I}_{N_{c}} \otimes \mathbf{F}_{m}^{\mathrm{T}}\right) \otimes \mathbf{W}_{m}^{*} \mathbf{h}_{\mathbf{c}}+\mathbf{e}_{m}}
ym=⎣⎢⎢⎢⎡ym[1]ym[2]⋮ym[N]⎦⎥⎥⎥⎤=
Sm(INc⊗FmT)⊗Wm∗hc+em 其中，
S
m
=
[
s
m
T
[
1
]
0
⋯
0
s
m
T
[
2
]
s
m
T
[
1
]
⋯
⋅
⋮
⋮
⋱
⋮
s
m
T
[
N
]
⋯
⋯
s
m
T
[
N
−
N
c
+
1
]
]
\mathbf{S}_{m}=\left[\begin{array}{cccc}{\mathbf{s}_{m}^{\mathrm{T}}[1]} & {0} & {\cdots} & {0} \\ {\mathbf{s}_{m}^{\mathrm{T}}[2]} & {\mathbf{s}_{m}^{\mathrm{T}}[1]} & {\cdots} & {\cdot} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\mathbf{s}_{m}^{\mathrm{T}}[N]} & {\cdots} & {\cdots} & {\mathbf{s}_{m}^{\mathrm{T}}\left[N-N_{\mathrm{c}}+1\right]}\end{array}\right]
Sm=⎣⎢⎢⎢⎡smT[1]smT[2]⋮smT[N]0smT[1]⋮⋯⋯⋯⋱⋯0⋅⋮smT[N−Nc+1]⎦⎥⎥⎥⎤。 这个式子笔者推过，没有问题。进一步地使用列化经典公式：
vec
(
A
B
C
)
=
(
C
T
⊗
A
)
vec
(
B
)
\operatorname{vec}(\mathbf{A B C})=\left(\mathbf{C}^{\mathrm{T}} \otimes \mathbf{A}\right) \operatorname{vec}(\mathbf{B})
vec(ABC)=(CT⊗A)vec(B) 有：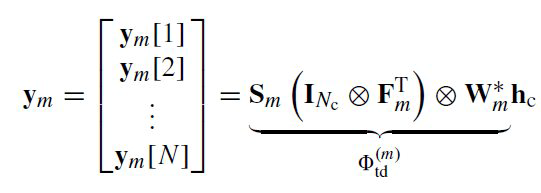 
再根据之前对
H
d
\mathbf{H}_\mathrm{d}
Hd的分解，可得：
y
m
=
Φ
t
d
(
m
)
(
I
N
c
⊗
A
‾
T
∘
A
R
)
[
γ
1
,
0
⋮
γ
N
p
,
0
⋮
γ
1
,
(
N
c
−
1
)
⋮
γ
N
p
,
(
N
c
−
1
)
]
+
e
\mathbf{y}_{m}=\Phi_{\mathrm{td}}^{(m)}\left(\mathbf{I}_{N_{\mathrm{c}}} \otimes \overline{\mathbf{A}}_{\mathrm{T}} \circ \mathbf{A}_{\mathrm{R}}\right)\left[\begin{array}{c}{\gamma_{1,0}} \\ {\vdots} \\ {\gamma_{N_{\mathrm{p}}, 0}} \\ {\vdots} \\ {\gamma_{1,\left(N_{\mathrm{c}}-1\right)}} \\ {\vdots} \\ {\gamma_{N_{\mathrm{p}}},\left(N_{\mathrm{c}}-1\right)}\end{array}\right]+\mathbf{e}
ym=Φtd(m)(INc⊗AT∘AR)⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡γ1,0⋮γNp,0⋮γ1,(Nc−1)⋮γNp,(Nc−1)⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤+e
这个形式就可以写成稀疏问题了，如下：
y m = Φ t d ( m ) ( I N c ⊗ A ‾ t x ⊗ A r x ) x ^ t d + e m \mathbf{y}_{m}=\Phi_{\mathrm{td}}^{(m)}\left(\mathbf{I}_{N_{\mathrm{c}}} \otimes \overline{\mathbf{A}}_{\mathrm{tx}} \otimes \mathbf{A}_{\mathrm{rx}}\right) \hat{\mathbf{x}}_{\mathrm{td}}+\mathbf{e}_{m} ym=Φtd(m)(INc⊗Atx⊗Arx)x^td+em 其中， A t x \mathbf{A}_{\mathrm{tx}} Atx和 A r x \mathbf{A}_{\mathrm{rx}} Arx是对应的码本，由 G t G_t Gt个量化的 a T ( θ ~ x ) \mathbf{a}_{\mathrm{T}}\left(\tilde{\theta}_{x}\right) aT(θ~x)和 G r G_r Gr个量化的 a R ( θ ~ x ) \mathbf{a}_{\mathrm{R}}\left(\tilde{\theta}_{x}\right) aR(θ~x)组成。 x ^ t d \hat{\mathbf{x}}_{\mathrm{td}} x^td的维度为 N c G r G t × 1 N_{\mathrm{c}} G_{\mathrm{r}} G_{\mathrm{t}} \times 1 NcGrGt×1。
详细说明下这个改写为稀疏过程的思路，首先假定发送和接收的角度是由码本中量化的角度里挑选的。这里当然会涉及一个精确度的问题，误差肯定是有的，但是不急。也就是说，一条路径可能有 G t × G r G_t\times G_r Gt×Gr种角度组成，而我们要估计的多径信道的径，就是在这 G t × G r G_t\times G_r Gt×Gr中找。而每一径的延时又有 N c N_c Nc种选择，综合了角度和延时，准确描述信道的一条径，就总共有 N c G r G t N_{\mathrm{c}} G_{\mathrm{r}} G_{\mathrm{t}} NcGrGt种可能性。这样一来， x ^ t d \hat{\mathbf{x}}_{\mathrm{td}} x^td就是一个极其稀疏的向量，而他的非零项就对应了实际的信道径。
按理到这一步，已经可以用压缩感知进行求解了，但作者进行了进一步的推导，先有： p d \mathbf{p}_d pd，每个元素为 p d ( n ) = p r c ( ( d − n N c G c ) T s ) p_{d}(n)=p_{\mathrm{rc}}\left(\left(d-n \frac{N_{\mathrm{c}}}{G_{\mathrm{c}}}\right) T_{\mathrm{s}}\right) pd(n)=prc((d−nGcNc)Ts)，for d = 1 , 2 , … , N c d=1,2, \ldots, N_{\mathrm{c}} d=1,2,…,Nc and n = 1 , 2 , … , G c n=1,2, \ldots, G_{\mathrm{c}} n=1,2,…,Gc。于是有
y m = Φ t d ( m ) ( I N c ⊗ A ‾ t x ⊗ A r x ) Γ x t d + e m \mathbf{y}_{m}=\Phi_{\mathrm{td}}^{(m)}\left(\mathbf{I}_{N_{\mathrm{c}}} \otimes \overline{\mathbf{A}}_{\mathrm{tx}} \otimes \mathbf{A}_{\mathrm{rx}}\right) \Gamma \mathbf{x}_{\mathrm{td}}+\mathbf{e}_{m} ym=Φtd(m)(INc⊗Atx⊗Arx)Γxtd+em 其中 Γ = [ I G r G t ⊗ p 1 T I G r G t ⊗ p 2 T ⋮ I G r G t ⊗ p N c T ] \Gamma=\left[\begin{array}{c}{\mathbf{I}_{G_{\mathrm{r}} G_{\mathrm{t}}} \otimes \mathbf{p}_{1}^{\mathrm{T}}} \\ {\mathbf{I}_{G_{\mathrm{r}} G_{\mathrm{t}}} \otimes \mathbf{p}_{2}^{\mathrm{T}}} \\ {\vdots} \\ {\mathbf{I}_{G_{\mathrm{r}} G_{\mathrm{t}}} \otimes \mathbf{p}_{N_{\mathrm{c}}}^{\mathrm{T}}}\end{array}\right] Γ=⎣⎢⎢⎢⎡IGrGt⊗p1TIGrGt⊗p2T⋮IGrGt⊗pNcT⎦⎥⎥⎥⎤ 那么 x t d ∈ C G c G r G t × 1 \mathbf{x}_{\mathrm{td}} \in \mathbb{C}^{G_{\mathrm{c}} G_{\mathrm{r}} G_{\mathrm{t}} \times 1} xtd∈CGcGrGt×1就是一个 N p N_p Np-稀疏的稀疏向量。我的理解是这样的，角度的组合还是 G t × G r G_t\times G_r Gt×Gr种没问题，但是延时的选择变成了更加细分的 p d p_{d} pd，而之前只能是整数延时。这样可以提高延时估计的精确度。最后，令 Φ t d = [ S 1 ( I N c ⊗ F f T ) ⊗ W 1 ∗ S 2 ( I N c ⊗ F 2 † ) ⊗ W 2 ∗ ⋮ S M ( I N c ⊗ F M T ) ⊗ W M ∗ ] ∈ C N M N R F × N c N r N t \Phi_{\mathrm{td}}=\left[\begin{array}{c}{\mathbf{S}_{1}\left(\mathbf{I}_{N_{\mathrm{c}}} \otimes \mathbf{F}_{\mathrm{f}}^{\mathrm{T}}\right) \otimes \mathbf{W}_{1}^{*}} \\ {\mathbf{S}_{2}\left(\mathbf{I}_{N_{\mathrm{c}}} \otimes \mathbf{F}_{2}^{\dagger}\right) \otimes \mathbf{W}_{2}^{*}} \\ {\vdots} \\ {\mathbf{S}_{M}\left(\mathbf{I}_{N_{\mathrm{c}}} \otimes \mathbf{F}_{M}^{\mathrm{T}}\right) \otimes \mathbf{W}_{M}^{*}}\end{array}\right] \in \mathbb{C}^{N M N_{\mathrm{RF}} \times N_{\mathrm{c}} N_{\mathrm{r}} N_{\mathrm{t}}} Φtd=⎣⎢⎢⎢⎢⎡S1(INc⊗FfT)⊗W1∗S2(INc⊗F2†)⊗W2∗⋮SM(INc⊗FMT)⊗WM∗⎦⎥⎥⎥⎥⎤∈CNMNRF×NcNrNt 和 Ψ t d = ( I N c ⊗ A ‾ t x ⊗ A r x ) Γ \Psi_{\mathrm{td}}=\left(\mathbf{I}_{N_{\mathrm{c}}} \otimes \overline{\mathbf{A}}_{\mathrm{tx}} \otimes \mathbf{A}_{\mathrm{rx}}\right) \Gamma Ψtd=(INc⊗Atx⊗Arx)Γ 可得， y t d = Φ t d Ψ t d x t d + e \mathbf{y}_{\mathrm{td}}=\Phi_{\mathrm{td}} \Psi_{\mathrm{td}} \mathbf{x}_{\mathrm{td}}+\mathbf{e} ytd=ΦtdΨtdxtd+e。
其中，估计过程中用到的beamformers F m , W m , m = 1 , 2 , ⋯ , M \mathbf{F}_{m}, \mathbf{W}_{m}, m=1,2, \cdots, M Fm,Wm,m=1,2,⋯,M是随机取的量化相位。
然后，通过把零范数放缩为一范数，优化问题可写为：
min x t d ∥ x t d ∥ 1 such that ∥ y t d − Φ t d Ψ t d x t d ∥ 2 ≤ ϵ \min _{\mathbf{x}_{\mathrm{td}}}\left\|\mathbf{x}_{\mathrm{td}}\right\|_{1} \quad \text { such that } \quad\left\|\mathbf{y}_{\mathrm{td}}-\Phi_{\mathrm{td}} \Psi_{\mathrm{td}} \mathbf{x}_{\mathrm{td}}\right\|_{2} \leq \epsilon xtdmin∥xtd∥1 such that ∥ytd−ΦtdΨtdxtd∥2≤ϵ
OMP算法可以用于解决此类问题，如果信道的径数 l l l已知，可以直接做 l l l次迭代求解。 如果未知，则迭代到一定范围后停止。一般取， ϵ = E [ e ∗ e ] \epsilon=\mathbb{E}\left[\mathbf{e}^{*} \mathbf{e}\right] ϵ=E[e∗e]。
频域估计方法接下来，作者又介绍了频域的方法，其实和时域大同小异。类似地，通过FFT，可以把频域信号写为：
y ˘ m [ k ] = W m ∗ H [ k ] F m s ˘ m [ k ] + e ˘ m [ k ] \breve{y}_{m}[k]=\mathbf{W}_{m}^{*} \boldsymbol{H}[k] \mathbf{F}_{m} \breve{\boldsymbol{s}}_{m}[k]+\breve{\boldsymbol{e}}_{m}[k] y˘m[k]=Wm∗H[k]Fms˘m[k]+e˘m[k] k k k 代表的是子载波index。 有： H [ k ] = ∑ ℓ = 1 N p α ℓ β k , ℓ a R ( ϕ ℓ ) a T ∗ ( θ ℓ ) H[k]=\sum_{\ell=1}^{N_{\mathrm{p}}} \alpha_{\ell} \beta_{k, \ell} \mathbf{a _ { \mathrm { R } }}\left(\phi_{\ell}\right) \mathbf{a}_{\mathrm{T}}^{*}\left(\theta_{\ell}\right) H[k]=ℓ=1∑Npαℓβk,ℓaR(ϕℓ)aT∗(θℓ) 其中， β k , ℓ = ∑ d = 0 N c − 1 p ( d T s − τ ℓ ) e − j 2 π k d R \beta_{k, \ell}=\sum_{d=0}^{N_{c}-1} p\left(d T_{\mathrm{s}}-\tau_{\ell}\right) e^{-\mathrm{j} \frac{2 \pi k d}{R}} βk,ℓ=∑d=0Nc−1p(dTs−τℓ)e−jR2πkd，然后，该问题可转化为稀疏问题求解： vec ( y ˘ m [ k ] ) = Φ f d ( m ) [ k ] ( A ‾ t x ⊗ A r x ) x ˇ [ k ] + e ˘ m [ k ] \operatorname{vec}\left(\breve{\boldsymbol{y}}_{m}[k]\right)=\Phi_{\mathrm{fd}}^{(m)}[k]\left(\overline{\mathbf{A}}_{\mathrm{tx}} \otimes \mathbf{A}_{\mathrm{rx}}\right) \check{x}[k]+\breve{e}_{m}[k] vec(y˘m[k])=Φfd(m)[k](Atx⊗Arx)xˇ[k]+e˘m[k] 其中， x ˇ [ k ] ∈ C G r G t × 1 \check{x}[k] \in \mathbb{C}^{G_{\mathrm{r}} G_{\mathrm{t}} \times 1} xˇ[k]∈CGrGt×1是个 N p N_p Np-稀疏的向量。
结合估计方法总结一下，时域和频域的估计方法其实都是在给定的码本内用OMP方法去接一个稀疏问题。
时域方法： 可以直接解出时域所有的信道时间响应，缺点在于整个稀疏问题过大，增大了算法复杂度。
频域方法：每个子载波上的估计问题很小，较易求解 ，但想完全恢复所有CSI要求K次。
结合方法：用频域方法求解角度信息，再用时域方法求解完整CSI。 首先，可以选取P个子载波， P ≤ K P\le K P≤K。对其分别进行频域估计，估计出角度值。将估出的角度值作为字典，再使用时域估计，估计完整的CSI。一言以蔽之，先用频域估计，缩小字典大小，再用时域估计解决问题。
相关阅读- 专栏： 混合波束成形
- 专栏： 智能反射面
- 混合波束成形|基础：深入浅出5G，毫米波，大规模MIMO与波束赋形
- 混合波束成形|进阶：深入浅出混合波束赋形
- 混合波束成形| 基于坐标迭代更新法的混合波束赋形算法
- 混合波束成形| 基于正交匹配追踪（Orthogonal Matching Pursuit）法的混合波束赋形算法
- 混合波束成形| 论文：基于MMSE准则的混合波束成形算法
- 混合波束成形| 通过天线空间方向图理解波束成形的物理意义
- 混合波束成形| 基于深度学习的大规模天线阵列混合波束成形设计
- 混合波束成形| MIMO系统的DFT码本
- 混合波束成形| HBF系统的克拉美罗下界
