文章目录
前言
- 前言
- 为什么要掌握CRLB
- 一些近期涉及CRLB的通信估计算法论文
- CRLB的简单介绍
- 通信中最重要的CRLB——高斯噪声建模下
- 矢量情形的CRLB
- 实数情形
- 复数情形：
- 相关阅读
在对通信系统估计问题的最新科研文章的调研中，我发现CRLB （克拉美罗下界）的出镜率非常高。这也说明了这一早就被提出的概念，至今能追随着潮流，也值得去掌握。 因此，简单地写了这篇文章来概述下 CRLB 与 科研中的估计算法。
为什么要掌握CRLB我总是觉得，在谈一个东西前，首先要说明为什么要学这个东西， 下面简单说明下CRLB的作用和功能。 CRLB的潜在使用场景： 界定各类估计算法的性能的upper bound 如果你掌握了CRLB的推导，可以有以下优点：
■ 1. 类似于去实现其他论文的算法，CRLB可以作为一条仿真图上的对比曲线。 ■ 2. 作为理论上界，与CRLB线的距离可以界定文章提出的新算法的优劣。 ■ 3. 对于许多新的算法框架，推导其下的CRLB本身就是文章的一个贡献点。 ■ 4. 在仿真中，与CRLB的gap值是否合理，可以帮助发现错误。
我认为，CRLB最大的优点在于，不论你的估计算法是什么场景，哪种问题，这都是一种可以复制的模式，一种泛用的方法。
一些近期涉及CRLB的通信估计算法论文
由于99%的通信问题都基于高斯噪声的假设，而这一假设非常便于我们推导求解CRLB所必要的PDF。因此，求解通信算法的CRLB就显得较为简单。 
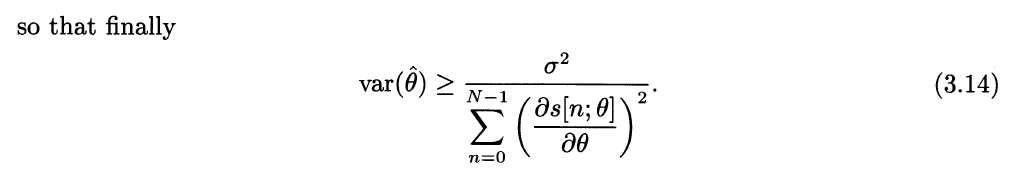
即先求出Fisher信息矩阵，再求逆，得到CRLB。
而在高斯噪声场景下，可以进一步特别地： 
绝大部分情况下，方差与估计参数无关时，上式可以进一步化简为：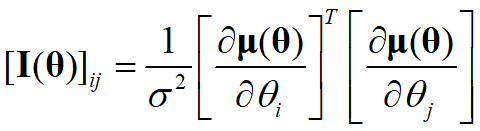 
Fisher信息矩阵 （I）由下式给出。
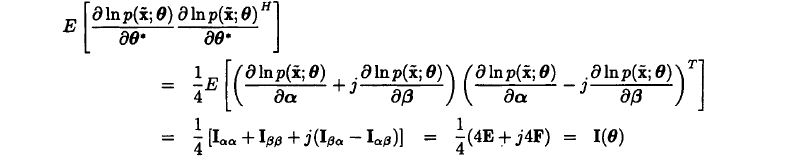
同样，在复高斯噪声情形下，可以特别地有：
- 专栏： 混合波束成形
- 专栏： 智能反射面
- 混合波束成形|基础：深入浅出5G，毫米波，大规模MIMO与波束赋形
- 混合波束成形|进阶：深入浅出混合波束赋形
- 混合波束成形| 基于坐标迭代更新法的混合波束赋形算法
- 混合波束成形| 基于正交匹配追踪（Orthogonal Matching Pursuit）法的混合波束赋形算法
- 混合波束成形| 论文：基于MMSE准则的混合波束成形算法
- 混合波束成形| 通过天线空间方向图理解波束成形的物理意义
- 混合波束成形| 基于深度学习的大规模天线阵列混合波束成形设计
- 混合波束成形| MIMO系统的DFT码本
- 混合波束成形| HBF系统的克拉美罗下界
