最近接触到OTFS这个技术概念， 于是找到一些相关的paper阅读了一下。 中间涉及许多的数学推导暂时还是一知半解，受限于自身水平，这篇相关的记录博客主要是个人理解，可能有所纰漏，希望大家指出。看了一些相关介绍的Magazine文章，最后发现还是提出者最开始的paper更容易理解，也即本文所围绕的文章： 《Orthogonal Time Frequency Space Modulation》 。总体感受是，对于高移动性场景，对于时变信道，OTFS确实是一种相比于传统OFDM系统更好的通信调制方式。
系统模型OTFS的核心思想建立于下式之上： 对于系统的输入信号 s ( t ) s(t) s(t)，有接收信号： r ( t ) = ∬ h ( τ , ν ) s ( t − τ ) e j 2 π ν ( t − τ ) d ν d τ (1) r(t)=\iint h(\tau, \nu) s(t-\tau) e^{j 2 \pi \nu(t-\tau)} \mathrm{d} \nu \mathrm{d} \tau \tag{1} r(t)=∬h(τ,ν)s(t−τ)ej2πν(t−τ)dνdτ(1) 这个式子我是这样理解的， 如果是传统的时域信号模型，此处接收信号应该是 h ( t ) h(t) h(t)与 s ( t ) s(t) s(t)的卷积，因此这里的 h ( τ , v ) h(\tau, v) h(τ,v)是类似于 h ( t ) h(t) h(t)这样的角色，代表定义在了多普勒-延时域 (分别对应 v v v和 τ \tau τ)上的信道响应。此外，由于用户的移动性造成的多普勒频移，带来了后面这一项 e j 2 π ν ( t − τ ) e^{j 2 \pi \nu(t-\tau)} ej2πν(t−τ)。这是因为用户的移动使得传输距离发生了变化，从而导致接收到信号相位的变化，反应为频率的变化，也即时变性的由来。 因此，式(1)刻画了这样一个时变的通信系统。 这里再多提一句，相比于时域模型，这里有两个维度： v v v和 τ \tau τ，这是因为延迟相同的两条径可能对应了不同的移动速度，因此也应视为两条径。 而在计算接收信号时，需要把这些径的结果一起累加，因此是一个二维积分的形式。
这里有必要再对这一在多普勒-延时域上的信道建模和传统的时域-频域 (多径造成的频率选择性通过频域刻画， 时变性由时域刻画) 的信道建模进行比较，来说明其鲜明的特点和优势。
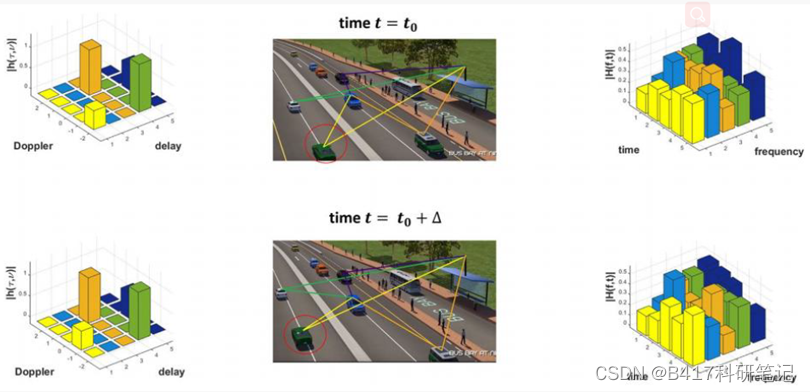上图展示了对于同一信道场景， 在两种不同刻画下的形式。 中间的具体场景图中，每根不同颜色的线所对应的真实传输路径，例如黄色线，在多普勒-延时域中只体现为一个黄色的柱。 这是因为只需要一对移动速度信息
v
v
v和延时
τ
\tau
τ就可以精确描述这一径的所有信息。 另一方面，由于移动性和多径造成的时变性和频选性， 在时频域的刻画中， 可以看到黄色的柱子贯穿了整个时域，也即需要用更多的信息量才能进行描述。 在《Orthogonal Time-Frequency Space Modulation: A Promising Next-Generation Waveform》这篇Magazine文章中，作者总结了多普勒-延时域的四大优点如下：
- 分离性： 不同的径可以被清晰地分离出来。 例如，即使延时相同的两条径，但由于其时变性不同，也会体现在多普勒-延时域的不同网格之上。 相反，在时频域中则较难被精准分离。
- 稳定性： 由于用户的移动性，和每径的传输距离的变化速度相对较慢， 因此对应的多普勒-延时域的信道响应也相对稳定，也即信道变化更慢。与之相对的，高速运动场景下，一个相干时间内很可能只能容纳3个OFDM信号，这将严重增大信道估计的负担。
- 简洁性： 多普勒域的描述相对更加简洁。 文章指出，对于无线通信系统存在 4 τ m a x v m a x ≤ 1 4\tau_{max}v_{max}\le 1 4τmaxvmax≤1，因此，延时域的坐标范围为 [ 0 , τ m a x ] [0,\tau_{max}] [0,τmax]，多普勒域的坐标范围为 [ − v m a x , v m a x ] [-v_{max}, v_{max}] [−vmax,vmax]，相对简洁。
- 潜在稀疏性： 从图中我们也可以看出，由于在高频传输中， 路径数往往是非常有限的，因此其在多普勒-延时域上的结果也将是稀疏的。即对于大部分的 v v v和 τ \tau τ，信道响应都是 0 0 0。相反，对于传统的时频域信道，每条径作用在不同的时间和频域上，因此并不体现稀疏性。
接下来，我们讲述下OTFS调制的具体过程。为便于理解，我们需要始终贯彻的一个思想是时刻将其与我们所熟悉的OFDM系统进行对标，从而能更深入地认识这一调制方式并理解其优越性所在。
OTFS的系统框图如下所示：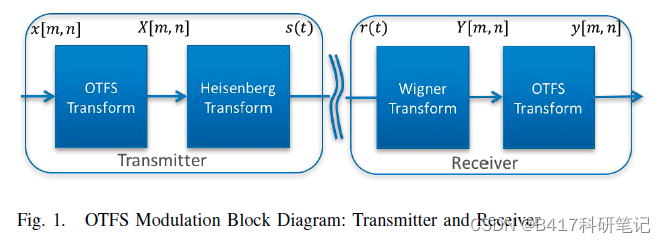 
首先，我们所要传输的原始数据流是多普勒-延时域上的
x
[
n
,
m
]
x[n,m]
x[n,m]， 我们将通过所谓的“OTFS transform”将其变换为时频域上的信号
X
[
n
,
m
]
X[n,m]
X[n,m]。这个OTFS transform包括了inverse symplectic Fourier transform和加窗操作，会在下文再详述。
接下来，通过对 X [ n , m ] X[n,m] X[n,m]进行 “Heisenberg transform”，可以将该调制信号转换为时域发送信号 s ( t ) s(t) s(t)。这一步我认为是对标OFDM系统中的IFFT操作，也即将一个时频域调制的信号变换为一个实际发送的时域信号模型。 紧接着， s ( t ) s(t) s(t)在信道中传输后，接收端需要对接收信号 r ( t ) r(t) r(t)进行一步“Wigner transform”，从而将该时域接收信号转换到时频域。这个“Wigner transform”是 “Heisenberg transform”的逆变换。因此，我认为这一步则是对标于OFDM系统中的FFT操作，与发送时的IFFT对应。最后，再次通过OTFS变换，将时频域信号转换到多普勒-延时域上的 y [ n , m ] y[n,m] y[n,m] 进行信号处理。
总结一下，相较于OFDM系统，OTFS需要在发送和接收处各多加一个OTFS转换，来完成在多普勒-延时域和时频域之间的变换。然而，核心的思路仍是类似的： 在更易进行信号处理的域上装载信息。 例如传统的OFDM系统，对于频选多径场景，直接在时域上进行信号处理将非常复杂。然而通过把信息装在在子载波上，由于每个子载波的平坦性，信号处理的难度将大幅降低。 相较于OFDM， OTFS则将时变性也考虑在内，并指出了在多普勒-时延域上进行信号处理的优势。 美中不足的是， 相较于OFDM中简单的FFT和IFFT操作， OTFS中所涉及的一系列Heisenberg transform等陌生的数学转换，实在是让人望而却步。然而这似乎也符合天下并无免费的午餐这一亘古不变的定律。接下来，让我们挑战一下这个OTFS的推导。
调制的细节 时频域调制我们先按照论文中的顺序，介绍将时频域信号 X [ n , m ] X[n,m] X[n,m]转换到时域信号 s ( t ) s(t) s(t)的具体操作。首先， X [ n , m ] X[n,m] X[n,m]是加载在如下时频网格上的信息： Λ = { ( n T , m Δ f ) , n , m ∈ Z } \Lambda=\{(n T, m \Delta f), \quad n, m \in \mathbb{Z}\} Λ={(nT,mΔf),n,m∈Z} 我们将有： s ( t ) = ∑ m = − M / 2 M / 2 − 1 ∑ n = 0 N − 1 X [ n , m ] g t x ( t − n T ) e j 2 π m Δ f ( t − n T ) (2) s(t)=\sum_{m=-M / 2}^{M / 2-1} \sum_{n=0}^{N-1} X[n, m] g_{\mathrm{tx}}(t-n T) e^{j 2 \pi m \Delta f(t-n T)} \tag{2} s(t)=m=−M/2∑M/2−1n=0∑N−1X[n,m]gtx(t−nT)ej2πmΔf(t−nT)(2) 其中， g t x g_{\mathrm{tx}} gtx是发送成形滤波器，在接收端有与之对应的接收成形滤波器，它们符合如下关系： ∫ g t x ∗ ( t ) g r x ( t − n T ) e j 2 π m Δ f ( t − n T ) d t = δ ( m ) δ ( n ) \int g_{\mathrm{tx}}^{*}(t) g_{\mathrm{rx}}(t-n T) e^{j 2 \pi m \Delta f(t-n T)} \mathrm{d} t=\delta(m) \delta(n) ∫gtx∗(t)grx(t−nT)ej2πmΔf(t−nT)dt=δ(m)δ(n) 从而可以消除symbol间的干扰。这里(2)中的时频域到时域的变换也被称为 Heisenberg transform。作者指出，这可以被看作 OFDM系统中将频域信号转化为时域的 一种拓展。因为主要目的是为了理解OTFS的核心思想，其中具体的数学推导笔者也没有深究。继续向下看，作者指出(2)式可以通过定义Heisenberg operator Π X ( ⋅ ) \Pi_{X}(\cdot) ΠX(⋅)， 从而改写为： s ( t ) = Π X ( g t x ) . s(t)=\Pi_{X}\left(g_{\mathrm{tx}}\right). s(t)=ΠX(gtx). 紧接着，结合(1)，接收信号可以表示为： r ( t ) = ∬ f ( τ , ν ) g t x ( t − τ ) e j 2 π ν ( t − τ ) d ν d τ + v ( t ) r(t)=\iint f(\tau, \nu) g_{\mathrm{tx}}(t-\tau) e^{j 2 \pi \nu(t-\tau)} \mathrm{d} \nu \mathrm{d} \tau+v(t) r(t)=∬f(τ,ν)gtx(t−τ)ej2πν(t−τ)dνdτ+v(t) 其中 v ( t ) v(t) v(t)代表了噪声，而 f ( τ , ν ) f(\tau, \nu) f(τ,ν)则由下式给出： f ( τ , ν ) = h ( τ , ν ) ∗ σ X [ n , m ] = ∑ m = − M / 2 M / 2 − 1 ∑ n = 0 N − 1 X [ n , m ] h ( τ − n T , ν − m Δ f ) e j 2 π ( ν − m Δ f ) n T . \begin{aligned} &f(\tau, \nu)=h(\tau, \nu) *_{\sigma} X[n, m]= \\ &\sum_{m=-M / 2}^{M / 2-1} \sum_{n=0}^{N-1} X[n, m] h(\tau-n T, \nu-m \Delta f) e^{j 2 \pi(\nu-m \Delta f) n T} . \end{aligned} f(τ,ν)=h(τ,ν)∗σX[n,m]=m=−M/2∑M/2−1n=0∑N−1X[n,m]h(τ−nT,ν−mΔf)ej2π(ν−mΔf)nT. 到这里已经相当迷茫了，我们先硬着头皮继续往下看。 在接收机一侧，对于接收到的信号，我们首先通过接受滤波器进行处理： A g r x , r ( τ , ν ) ≜ ∫ g r ∗ ( t − τ ) r ( t ) e − j 2 π ν ( t − τ ) d t A_{g_{\mathrm{rx}}, r}(\tau, \nu) \triangleq \int g_{r}^{*}(t-\tau) r(t) e^{-j 2 \pi \nu(t-\tau)} \mathrm{d} t Agrx,r(τ,ν)≜∫gr∗(t−τ)r(t)e−j2πν(t−τ)dt 然后对其进行采样，得到： Y [ n , m ] = A g r x , r ( τ , ν ) ∣ τ = n T , ν = m Δ f Y[n, m]=\left.A_{g_{\mathrm{rx}}, r}(\tau, \nu)\right|_{\tau=n T, \nu=m \Delta f} Y[n,m]=Agrx,r(τ,ν)∣τ=nT,ν=mΔf 该变换也被称为Wigner transform。据此我们可以最终推导得到这样的一个端到端的表达式: Y [ n , m ] = H [ n , m ] X [ n , m ] (3) Y[n, m]=H[n, m] X[n, m] \tag{3} Y[n,m]=H[n,m]X[n,m](3) 其中， H [ n , m ] H[n, m] H[n,m]由下式给出： H [ n , m ] = ∬ h ( τ , ν ) e j 2 π ν n T e − j 2 π ( ν + m Δ f ) τ d ν d τ (4) H[n, m]=\iint h(\tau, \nu) e^{j 2 \pi \nu n T} e^{-j 2 \pi(\nu+m \Delta f) \tau} \mathrm{d} \nu \mathrm{d} \tau \tag{4} H[n,m]=∬h(τ,ν)ej2πνnTe−j2π(ν+mΔf)τdνdτ(4) (3)式中揭示了，使用OTFS调制，收发信号之间的关系与OFDM系统非常类似，也是直接相乘，有利于信号处理的简便性。 通过(3)式，我不禁有个疑问， 似乎直接从时频域进行传输信息就可以了，何必多此一举，非要在多普勒-延时域进行呢？ 这是因为， (4)中所给出的 H H H的形式非常复杂，而在下一节我们将看到，通过OTFS调制可以对信道的表达式进行大幅的简化。
OTFS的调制与解调上一小节中，说明了时频发送信号 X [ n , m ] X[n,m] X[n,m]与接收信号 Y [ n , m ] Y[n,m] Y[n,m]间的简单关系，尽管推导复杂，但结果是简洁的。 这一节中，需要补上OFTS系统的最后一步，即多普勒-时延域信号与时频域信号间的转换，也即OTFS-transform。 首先，我们以 X p [ n , m ] X_{p}[n, m] Xp[n,m]来表示 X [ n , m ] X[n, m] X[n,m]的周期版本，其中周期为 ( N , M ) (N,M) (N,M)，那么有 Symplectic Finite Fourier Transform (SFFT) 定义如下： x p [ k , l ] = ∑ n = 0 N − 1 ∑ m = − M 2 M 2 − 1 X p [ n , m ] e − j 2 π ( n k N − m l M ) x_{p}[k, l]=\sum_{n=0}^{N-1} \sum_{m=-\frac{M}{2}}^{\frac{M}{2}-1} X_{p}[n, m] e^{-j 2 \pi\left(\frac{n k}{N}-\frac{m l}{M}\right)} xp[k,l]=n=0∑N−1m=−2M∑2M−1Xp[n,m]e−j2π(Nnk−Mml) 我将其与普通的2D-FFT的式子进行了对比： F ( u , v ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) e − j 2 π ( u x / M + v y / N ) F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) e^{-j 2 \pi(u x / M+v y / N)} F(u,v)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(ux/M+vy/N) 发现差别似乎不大。其逆变换则定义为： X p [ n , m ] = 1 M N ∑ l , k x [ k , l ] e j 2 π ( n k N − m l M ) X_{p}[n, m]=\frac{1}{M N} \sum_{l, k} x[k, l] e^{j 2 \pi\left(\frac{n k}{N}-\frac{m l}{M}\right)} Xp[n,m]=MN1l,k∑x[k,l]ej2π(Nnk−Mml) 类似于圆周卷积的性质，有: SFFT ( X 1 [ n , m ] ⊛ X 2 [ n , m ] ) = SFFT ( X 1 [ n , m ] ) ⋅ SFFT ( X 2 [ n , m ] ) , \operatorname{SFFT}\left(X_{1}[n, m] \circledast X_{2}[n, m]\right)=\operatorname{SFFT}\left(X_{1}[n, m]\right) \cdot \operatorname{SFFT}\left(X_{2}[n, m]\right) \text {, } SFFT(X1[n,m]⊛X2[n,m])=SFFT(X1[n,m])⋅SFFT(X2[n,m]),
接下来，考虑一组QAM信息符号，将其安置在2D网格上，得到多普勒-延时域的发送信息 x [ k , l ] , k = 0 , … , N − 1 , l = 0 , ⋯ , M − 1 x[k, l], k=0, \ldots, N-1, l=0,\cdots, M-1 x[k,l],k=0,…,N−1,l=0,⋯,M−1。通过进行Heisenberg transform可以得到时频域信号，即: X [ n , m ] = W t x [ n , m ] SFFT − 1 ( x [ k , l ] ) X[n, m]=W_{\mathrm{tx}}[n, m] \operatorname{SFFT}^{-1}(x[k, l]) X[n,m]=Wtx[n,m]SFFT−1(x[k,l]) 这里 W t x [ n , m ] W_{\mathrm{tx}}[n, m] Wtx[n,m]传输窗函数。注意到上式可以再展开为： X [ n , m ] = 1 M N W t r [ n , m ] ∑ k = 0 N − 1 ∑ l = 0 M − 1 x [ k , l ] b k , l [ n , m ] b k , l [ n , m ] = e − j 2 π ( m l M − n k N ) \begin{aligned} X[n, m]=& \frac{1}{M N} W_{t r}[n, m] \sum_{k=0}^{N-1} \sum_{l=0}^{M-1} x[k, l] b_{k, l}[n, m] \\ b_{k, l}[n, m]&=e^{-j 2 \pi\left(\frac{m l}{M}-\frac{n k}{N}\right)} \end{aligned} X[n,m]=bk,l[n,m]MN1Wtr[n,m]k=0∑N−1l=0∑M−1x[k,l]bk,l[n,m]=e−j2π(Mml−Nnk) 因此，这可以视为将符号 x [ k , l ] x[k,l] x[k,l]调制到了一组二维基函数 b k , l [ n , m ] b_{k, l}[n, m] bk,l[n,m]之上，也即 X [ n , m ] X[n, m] X[n,m]中包含了不同 k , l k,l k,l对应的符号信息，是一种自然的分集。
同时，在接收端则是镜像的类似操作： Y W [ n , m ] = W r x [ n , m ] Y [ n , m ] Y p [ n , m ] = ∑ k , l = − ∞ ∞ Y W [ n − k N , m − l M ] \begin{gathered} Y_{W}[n, m]=W_{\mathrm{rx}}[n, m] Y[n, m] \\ Y_{p}[n, m]=\sum_{k, l=-\infty}^{\infty} Y_{W}[n-k N, m-l M] \end{gathered} YW[n,m]=Wrx[n,m]Y[n,m]Yp[n,m]=k,l=−∞∑∞YW[n−kN,m−lM] 可以得到： x ^ [ l , k ] = y [ l , k ] = SFFT ( Y p [ n , m ] ) ， \hat{x}[l, k]=y[l, k]=\operatorname{SFFT}\left(Y_{p}[n, m]\right)， x^[l,k]=y[l,k]=SFFT(Yp[n,m])， 根据一系列推导，作者得出如下结论： x ^ [ k , l ] = 1 M N ∑ m = 0 M − 1 ∑ n = 0 N − 1 x [ n , m ] h w ( k − n N T , l − m M Δ f ) (5) \hat{x}[k, l]=\frac{1}{M N} \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} x[n, m] h_{w}\left(\frac{k-n}{N T}, \frac{l-m}{M \Delta f}\right) \tag{5} x^[k,l]=MN1m=0∑M−1n=0∑N−1x[n,m]hw(NTk−n,MΔfl−m)(5) 其中， h w ( k − n N T , l − m M Δ f ) = h w ( ν ′ , τ ′ ) ∣ ν ′ = k − n N T , τ ′ = l − m M Δ f h_{w}\left(\frac{k-n}{N T}, \frac{l-m}{M \Delta f}\right)=\left.h_{w}\left(\nu^{\prime}, \tau^{\prime}\right)\right|_{\nu^{\prime}=\frac{k-n}{N T}, \tau^{\prime}=\frac{l-m}{M \Delta f}} hw(NTk−n,MΔfl−m)=hw(ν′,τ′)∣ν′=NTk−n,τ′=MΔfl−m h w ( ν ′ , τ ′ ) = ∬ h ( τ , ν ) w ( ν ′ − ν , τ ′ − τ ) e − j 2 π ν τ d τ d ν h_{w}\left(\nu^{\prime}, \tau^{\prime}\right)=\iint h(\tau, \nu) w\left(\nu^{\prime}-\nu, \tau^{\prime}-\tau\right) e^{-j 2 \pi \nu \tau} \mathrm{d} \tau \mathrm{d} \nu hw(ν′,τ′)=∬h(τ,ν)w(ν′−ν,τ′−τ)e−j2πντdτdν
这里定义略多，我们直接看(5)这个式子，注意到 ∀ k , l \forall k,l ∀k,l， x ^ [ k , l ] \hat{x}[k, l] x^[k,l]中均包含了 x [ k , l ] h w ( 0 , 0 ) x[k,l]h_w(0,0) x[k,l]hw(0,0)这一项，而剩下的则是符号间的干扰。作者指出，当延时、多普勒扩展和窗函数满足一定条件时有， h w ( k − n N T , l − m M Δ f ) ≈ 0 ∀ n ≠ k , m ≠ l h_{w}\left(\frac{k-n}{N T}, \frac{l-m}{M \Delta f}\right) \approx 0 \forall n \neq k, m \neq l hw(NTk−n,MΔfl−m)≈0∀n=k,m=l 此时将不再有符号间干扰，也即: x ^ [ k , l ] = x [ k , l ] h w ( 0 , 0 ) \hat{x}[k, l] =x[k,l]h_w(0,0) x^[k,l]=x[k,l]hw(0,0) 这就是说，对于多普勒-延时域的所有发送符号，可以视为经历的是相同的常量信道 h w ( 0 , 0 ) h_w(0,0) hw(0,0)，这将大大简化信号处理的难度。
后记目前暂时只对OTFS这一技术有一个粗浅的认知，尤其对其中的数学推导还没有深入探索。 后续如果有时间的话再深耕下。
