【深度强化学习】策略梯度 Policy Gradients

前言

重读《Deep Reinforcemnet Learning Hands-on》， 常读常新， 极其深入浅出的一本深度强化学习教程。 本文的唯一贡献是对其进行了翻译和提炼， 加一点自己的理解组织成一篇中文笔记。

原英文书下载地址: 传送门 原代码地址： 传送门

本文是书本第九章，介绍DQN的一种替代：策略梯度方法。

values 和 policy

在DQN方法中，我们主要是通过深度网络，得到不同状态下不同动作所对应的Q值，然后选取Q值最大的动作。 这一策略我们可以表示如下：

π ( s ) = arg ⁡ m a x a Q ( s , a ) \pi(s)=\arg m a x_{a} Q(s, a) π(s)=argmaxa​Q(s,a)

然而这其实表明了一件事， 我们真正希望得到的是策略本身， 而并不是Q值，Q值是用来做出决策的。这不禁让我们想到，能否直接去获得策略，而不是间接地先通过Q值计算再获得策略呢？

这样做又如下的三个好处：

1. 更直接。 自然，也有望带来更快的速度。
2. 更适用于连续动作空间。 在DQN中，我们需要对每个动作都计算一个Q值，然而如果动作空间是连续而非离散的，那么就相当于有无数个动作，显然不可能求出所有的Q值。
3. 策略学习类方法会引入随机性。具体而言，策略将被描述为动作的概率分布。 这在接下来会有所介绍，这对于网络的训练是有很大帮助的。

策略的表示

怎样表示一个策略？ 最直观的做法是设计这样一个函数： 输入观测状态， 输出选取的动作结果。 然而，更好的做法则是：输出所有动作的概率分布（此处我们暂时仍假定离散的动作空间）。这个函数往往通过神经网络拟合，下图展示了一个例子：

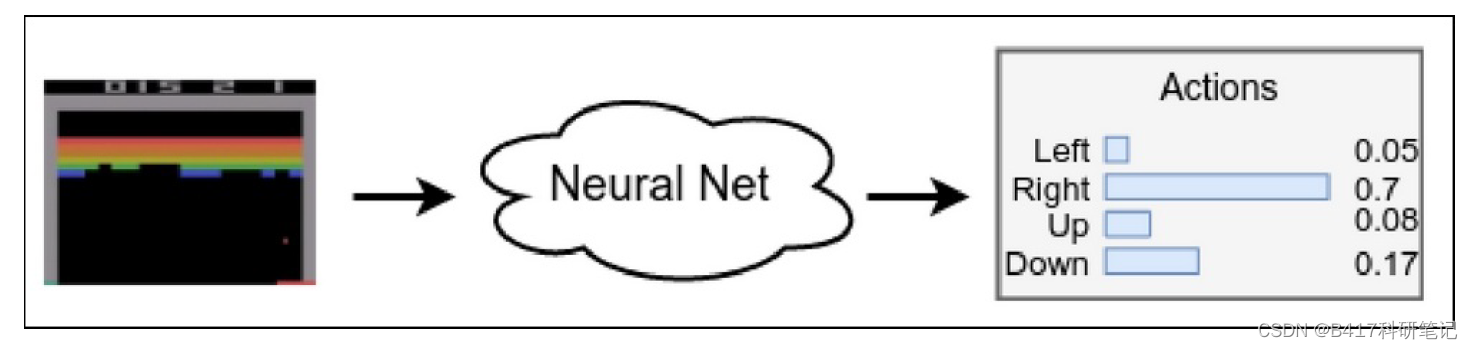这样做有诸多的好处：

1. 如果是传统的直接输出单个动作结果的设计， 那么神经网络的微小变化也可能会导致输出结果的跳变，非常不稳定。 相反，如果以概率分布作为输出，那么网络的微小变化也只会导致概率分布的微小变化，比较稳定。 这非常契合神经网络梯度下降的本质。
2. 由于策略是一个概率分布的结果，因此天然带有了探索的特性——即不存在说某一个动作绝不可能被选到的情况。

策略梯度

我们将策略梯度 (policy gradients, PG) 定义如下：

L = − Q ( s , a ) log ⁡ π ( a ∣ s ) \mathcal{L}=-Q(s, a) \log \pi(a \mid s) L=−Q(s,a)logπ(a∣s)

其中 Q ( s , a ) Q(s,a) Q(s,a)可以代表在状态 s s s下选用动作 a a a的价值（越大代表该动作越好），而 π ( a ∣ s ) \pi(a\mid s) π(a∣s)则代表我们的策略里此时选用该动作 a a a的概率。 值得一提的是，虽然名为策略梯度， 但 L \mathcal{L} L更多地被作为优化目标即损失函数来使用。 具体而言，我们期望在网络训练的过程中 (即对应策略 π \pi π的更新）能不断地最小化 L \mathcal{L} L，而这就要求对应于大 Q Q Q值的动作 a a a，其选取的概率 π ( a ∣ s ) \pi(a\mid s) π(a∣s)也应较大。 (log是一个单调增函数） 而这也就契合了我们的目标。

REINFORCE method

据此，我们可以得到策略梯度方法下的强化学习步骤：

1. 随机初始化神经网络
2. 进行N个回合， 保存数据 (s, a, r, s’)
3. 对于第 k k k个回合的step t t t， 计算Q值为： Q k , t = ∑ i = 0 γ i r i Q_{k, t}=\sum_{i=0} \gamma^{i} r_{i} Qk,t​=∑i=0​γiri​
4. 计算损失函数： L = − ∑ k , t Q k , t log ⁡ ( π ( a k , t ∣ s k , t , ) ) \mathcal{L}=-\sum_{k, t} Q_{k, t} \log \left(\pi\left(a_{k, t}\mid s_{k, t},\right)\right) L=−∑k,t​Qk,t​log(π(ak,t​∣sk,t​,))
5. 训练网络，最小化 L \mathcal{L} L
6. 从步骤2开始重复，直到收敛。

简单解释一下，这里用贝尔曼公式来计算Q值。 此外，注意到策略 π \pi π实质上就是神经网络： 接收 s s s，输出 a a a的概率。

实例：CartPole

以REINFORCE method 训练 CartPole游戏的代码在Chapter09/02_cartpole_reinforce.py之中。

首先：

class PGN(nn.Module):
	def __init__(self, input_size, n_actions):
		super(PGN, self).__init__()
		self.net = nn.Sequential(
		nn.Linear(input_size, 128),
		nn.ReLU(),
		nn.Linear(128, n_actions)
		)
	def forward(self, x):
		return self.net(x)

这里定义了我们要训练的神经网络，注意到，输出维度为动作空间维度， 输入维度为观测维度。 值得一提的是，我们本期望的输出是所有动作的概率分布，那么照例应当使用softmax函数来进行归一。然而，出于计算复杂度等的考虑，作者将直接使用 log_softmax计算损失函数，因此这里就省略掉了。我们只要记住这里其实期望输出的就是不同动作的概率分布即可。

下面是训练程序部分：

optimizer.zero_grad()
states_v = torch.FloatTensor(batch_states)
batch_actions_t = torch.LongTensor(batch_actions)
batch_qvals_v = torch.FloatTensor(batch_qvals)

logits_v = net(states_v)
log_prob_v = F.log_softmax(logits_v, dim=1)
log_prob_actions_v = batch_qvals_v * log_prob_v[range(len(batch_states)), batch_actions_t]
loss_v = -log_prob_actions_v.mean()

loss_v.backward()
optimizer.step()

其中，states_v , batch_actions_t 和batch_qvals_v 是通过与env环境交互后得到的状态、动作和对应的Q值，Q值由贝尔曼公式计算得到。此处最关键的语句是： log_prob_actions_v = batch_qvals_v * log_prob_v[range(len(batch_states)), batch_actions_t] 这也是神经网络的损失函数 （log_prob_v 是神经网络输出的函数）。 具体而言，由于CartPole是一个动作空间只有2的环境，因此，net的输出也是一个2维向量，分别代表了选取两个动作的概率。log_prob_v[range(len(batch_states)), batch_actions_t]这里就是提取出实际所采用的动作所对应的概率值结果，再与该动作对应的Q值相乘。 这样一来，如果我们要最小化损失函数，就是最大化Q值与该动作的乘积结果。 我们就可以将Q值理解为这一动作的选取概率的权重，Q值越大的动作，网络也将向着提升该动作选取概率的方向训练，也即达到了我们强化学习的目的。

这份代码非常清晰，建议大家自己去调试学习。