- 目录
- 概率的统计定义
- 大数定律
- 蒙特卡洛方法
- 动态规划方法的缺陷
- 相关参考
本节从概率的统计定义、大数定律的角度介绍蒙特卡洛方法的思想，并简单介绍针对动态规划方法求解强化学习任务的问题和解决方法。
概率的统计定义在一定条件下重复做 N N N次试验， N a N_a Na为 N N N次试验中事件 A A A发生的次数。随着次数 N N N的不断增大， N a N \frac{N_a}{N} NNa的结果逐渐稳定于某一具体数值 p p p附近。称数值 p p p为事件 A A A在该条件下发生的概率。
以投掷一枚质地均匀的硬币为例： 我们在不考虑极特殊情况(如硬币站立、卡在缝隙)，投掷硬币后，正面和反面向上的概率均为 1 2 \frac{1}{2} 21。如何验证这个结果？根据概率的统计定义，我们进行如下设定：
- 试验：投掷硬币；
- 事件 A A A：硬币正面向上；
- N a N_a Na： N N N次试验中事件 A A A发生的次数
随着试验次数 N N N的增加， N a N \frac{N_a}{N} NNa结果变化设计代码如下：
import random
import matplotlib.pyplot as plt
l = []
mean_l = []
for i in range(10000):
a = random.randint(0,1)
l.append(a)
if len(l) % 20 == 0:
mean_l.append(sum(l) / len(l))
x_l = [i for i in range(len(mean_l))]
plt.plot(x,[0.5 for i in x])
plt.plot(x,mean_l)
plt.show()
返回结果： 
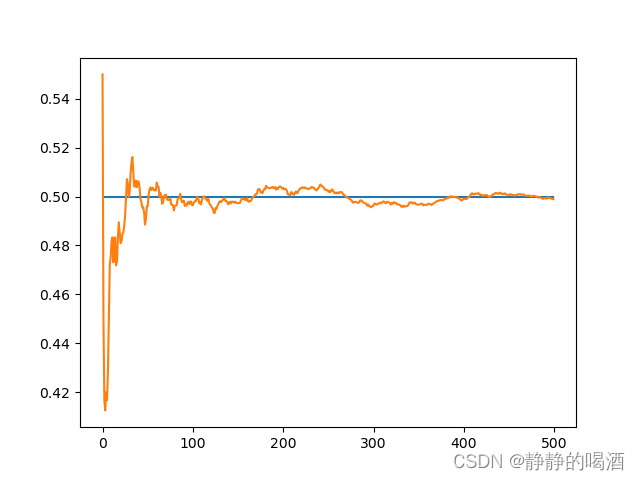通过上述图片观察可知：随着试验次数的增加，
N
a
N
\frac{N_a}{N}
NNa逐渐收敛于数值0.5附近。 我们可以从上述试验中发现：质地均匀的硬币，投掷硬币正面朝上的概率
P
u
p
=
0.5
P_{up} = 0.5
Pup=0.5，是确定性事件；而在试验中投掷硬币，是随机性事件(试验之前并不清楚事件
A
A
A是否发生)。概率的统计定义就是在条件不变的情况下，重复执行大量试验，对大量随机性事件结果统计事件发生的频率来近似该事件的概率结果。
蒙特卡洛方法本身也是通过随机性试验解决确定性问题。
大数定律介绍蒙特卡洛方法绕不开大数定律(Law of Large Numbers)。通俗的理解大数定律，即在试验条件不变的情况下，在随机事件大量重复出现中，往往存在必然的规律。 在各随机变量是独立同分布的条件下，大量重复试验中产生的随机变量的算数平均值向数学期望的算数平均值收敛的定律。
构建如下示例： 设计三个质地不均匀的骰子(随机投掷骰子各个面朝上的概率存在差异)其骰子点数和对应概率如下：
点数骰子 X 1 X_1 X1对应概率骰子 X 2 X_2 X2对应概率骰子 X 3 X_3 X3对应概率10.10.10.320.20.30.130.20.10.140.20.10.150.10.30.160.20.10.3手动计算一下三个质地不同的骰子对应的期望点数(各自数学期望的算数平均值)：[ N N N表示试验次数， x i x_i xi表示骰子 X X X产生的具体点数， p ( x i ) p(x_i) p(xi)表示点数对应的概率] E [ X ] = 1 N ∑ i = 1 N p ( x i ) × x i \mathbb E[X] = \frac{1}{N}\sum_{i=1}^Np(x_i)\times x_i E[X]=N1i=1∑Np(xi)×xi 骰子1： E [ X 1 ] = 1 6 × ( 0.1 × 1 + 0.2 × 2 + 0.2 × 3 + 0.2 × 4 + 0.1 × 5 + 0.2 × 6 ) = 3.6 \begin{aligned} \mathbb E[X_1] & = \frac{1}{6} \times(0.1 \times 1 + 0.2 \times 2 + 0.2 \times 3 + 0.2 \times 4 + 0.1 \times 5 + 0.2 \times 6) \\ & = 3.6 \end{aligned} E[X1]=61×(0.1×1+0.2×2+0.2×3+0.2×4+0.1×5+0.2×6)=3.6 骰子2： E [ X 2 ] = 1 6 × ( 0.1 × 1 + 0.3 × 2 + 0.1 × 3 + 0.1 × 4 + 0.3 × 5 + 0.1 × 6 ) = 3.5 \begin{aligned} \mathbb E[X_2] & = \frac{1}{6} \times(0.1 \times 1 + 0.3 \times 2 + 0.1 \times 3 + 0.1 \times 4 + 0.3 \times 5 + 0.1 \times 6) \\ & = 3.5 \end{aligned} E[X2]=61×(0.1×1+0.3×2+0.1×3+0.1×4+0.3×5+0.1×6)=3.5 骰子3： E [ X 3 ] = 1 6 × ( 0.1 × 1 + 0.1 × 2 + 0.1 × 3 + 0.1 × 4 + 0.3 × 5 + 0.3 × 6 ) = 4.3 \begin{aligned} \mathbb E[X_3] & = \frac{1}{6} \times(0.1 \times 1 + 0.1 \times 2 + 0.1 \times 3 + 0.1 \times 4 + 0.3 \times 5 + 0.3 \times 6) \\ & = 4.3 \end{aligned} E[X3]=61×(0.1×1+0.1×2+0.1×3+0.1×4+0.3×5+0.3×6)=4.3 现在对不同骰子进行重复投掷试验，试验代码设计如下：
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(1,7)
rate_l = [0.1,0.1,0.1,0.1,0.3,0.3]
rate_l2 = [0.1,0.3,0.1,0.1,0.3,0.1]
rate_l3 = [0.1,0.2,0.2,0.2,0.1,0.2]
def get_parameter(rate_l,exp_num):
l = []
mean_l = []
for i in range(exp_num):
a_1 = int(np.random.choice(x, size=1, replace=False, p=rate_l))
l.append(a_1)
if len(l) % 20 == 0:
mean_l.append(sum(l) / len(l))
return mean_l
def draw_picture(exp_num):
mean_l1 = get_parameter(rate_l,exp_num)
mean_l2 = get_parameter(rate_l2,exp_num)
mean_l3 = get_parameter(rate_l3,exp_num)
x = [i for i in range(len(mean_l1))]
plt.plot(x,mean_l1)
plt.plot(x,mean_l2)
plt.plot(x,mean_l3)
plt.show()
if __name__ == '__main__':
draw_picture(10000)
返回结果如下：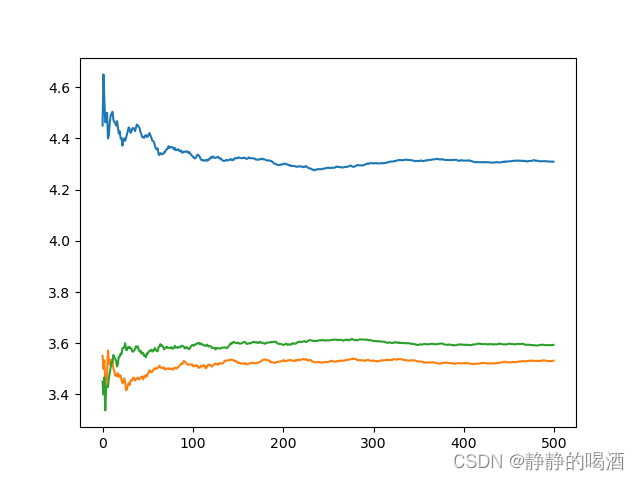 
可以观察到，随着重复试验次数的增加，骰子所产生随机变量的算数平均值向各自对应数学期望的算数平均值方向收敛。
蒙特卡洛方法(Monte Carlo method)也称统计模拟法、统计试验法，是把概率现象作为研究对象的数值模拟方法。根据大数定律的逻辑，蒙特卡洛方法主要通过简单的概率统计模型，针对所求问题的概率分布/数学期望，通过随机抽样、统计试验的方式，对采样结果求均值以近似问题的解。 根据上面的描述，我们对蒙特卡洛方法有如下认识：
- 所求问题特征存在缺失，导致没有办法直接求解其准确的概率分布或数学期望；
- 通过蒙特卡洛方法求得的解是近似解,并且该近似解恰好是所求问题的概率分布或数学期望；
- 蒙特卡洛方法通过大量的随机抽样和统计试验的方式进行求解。
我们在介绍动态规划方法过程中，主要依据的是贝尔曼期望方程自身满足不动点定理，通过自身不断迭代从而获取最优策略和最优价值函数，伴随广义策略迭代思想，我们可以获得鲁棒性强，准确性高的最优价值函数和最优策略。 V π ( s ) = ∑ a ∈ A π ( a ∣ s ) ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V π ( s ′ ) ] V_\pi(s) = \sum_{a \in \mathcal A}\pi(a \mid s))\sum_{s',r}p(s',r \mid s,a)[r + \gamma V_\pi(s')] Vπ(s)=a∈A∑π(a∣s))s′,r∑p(s′,r∣s,a)[r+γVπ(s′)] 但是，动态规划方法必须要求环境模型 → p ( s ′ , r ∣ s , a ) \to p(s',r \mid s,a) →p(s′,r∣s,a)已知的情况下才避免对环境采样进行求解。但实际任务中，完整的环境模型是很难获取到的，因此无法使用动态规划方法进行求解。
我们发现，动态特性函数未知条件下的强化学习任务恰好满足使用蒙特卡洛方法的条件：
- 由于动态特性函数未知/不完全可知 → \to → 无法精确求解状态 s s s的价值函数 V π ( s ) , q π ( s , a ) V_\pi(s),q_\pi(s,a) Vπ(s),qπ(s,a)；
- 价值函数本身就是 G t G_t Gt对于策略 π \pi π在不同条件(状态、动作条件)下的期望结果，正好是蒙特卡洛方法的求解目标； V π ( s ) = E π [ G t ∣ S t = s ] q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] \begin{aligned} V_\pi(s) & = \mathbb E_{\pi}[G_t \mid S_t = s] \\ q_\pi(s,a) & = \mathbb E_{\pi}[G_t \mid S_t = s,A_t = a] \end{aligned} Vπ(s)qπ(s,a)=Eπ[Gt∣St=s]=Eπ[Gt∣St=s,At=a]
- 即便我们不清楚系统内部如何执行状态转移操作的，但这并不影响状态转移操作的执行。可以通过大量重复试验获取状态转移过程的样本，使用蒙特卡洛方法在动态特性函数未知的情况下直接近似求解价值函数。
V π ( s ) = E π [ G t ∣ S t = s ] ≈ 1 N ∑ i = 1 N G t ( i ) V_\pi(s) = \mathbb E_{\pi}[G_t \mid S_t = s] \approx \frac{1}{N}\sum_{i=1}^N G_t^{(i)} Vπ(s)=Eπ[Gt∣St=s]≈N1i=1∑NGt(i)
下一节将介绍如何使用蒙特卡洛方法求解强化学习任务。
相关参考蒙特卡洛法 - 百度百科 用大数定律和蒙特卡洛法计算积分——概率与统计思想的巧妙应用 【强化学习】蒙特卡洛方法-前情回顾
