- 目录
- 回顾
- 概念介绍
- 蒙特卡洛方法采样方式
- 首次访问型与每次访问型
- 首次访问型算法示例
- 蒙特卡洛方法样本存储方式
上一节简单介绍了蒙特卡洛方法的基本思想，本节将介绍基于蒙特卡洛方法的策略评估过程
回顾在介绍动态规划求解强化学习任务中提到过，需要在动态特性函数已知的条件下，才能使用贝尔曼期望方程进行迭代求解。但在实际情况中，动态特性函数 p ( s ′ , r ∣ s , a ) p(s',r \mid s,a) p(s′,r∣s,a)未知/不完全可知，导致贝尔曼期望方程无法发挥作用。 V π ( s ) = ∑ a ∈ A π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V π ( s ′ ) ] V_\pi(s) = \sum_{a \in \mathcal A}\pi(a \mid s)\sum_{s',r}p(s',r \mid s,a)[r + \gamma V_\pi(s')] Vπ(s)=a∈A∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γVπ(s′)] 因此，只能针对 V π ( s ) V_\pi(s) Vπ(s)定义本身 → s \to s →s状态确定的条件下， 回报(Return)在 π \pi π策略下的期望。使用蒙特卡洛方法通过样本均值逼近期望结果(大数定律)。 V π ( s ) ≜ E π [ G t ∣ S t = s ] ≈ 1 N ∑ i = 1 N G t ( i ) V_\pi(s) \triangleq \mathbb E_{\pi}[G_t \mid S_t = s] \approx \frac{1}{N} \sum_{i=1}^N G_t^{(i)} Vπ(s)≜Eπ[Gt∣St=s]≈N1i=1∑NGt(i)
概念介绍蒙特卡洛方法本质上是基于通过采样大量数据来进行学习的经验方法实现的，因此，即便是在环境模型 p ( s ′ , r ∣ s , a ) p(s',r \mid s,a) p(s′,r∣s,a)未知/未完全可知的情况下，采用时间步骤有限的、完整情节(episode)中进行采样，并通过平均采样回报来解决强化学习问题。
一个情节 是如何被定义的？ 设定状态集合 S \mathcal S S，动作集合 A \mathcal A A，奖励集合 R \mathcal R R均属于离散型随机变量； S = { s [ 1 ] , s [ 2 ] , s [ 3 ] , . . . , s [ n ] } A = { a [ 1 ] , a [ 2 ] , a [ 3 ] , . . . , a [ m ] } R = { r [ 1 ] , r [ 2 ] , r [ 3 ] , . . . , r [ k ] } \begin{aligned} \mathcal S & = \{s^{[1]},s^{[2]},s^{[3]},...,s^{[n]}\} \\ \mathcal A & = \{a^{[1]},a^{[2]},a^{[3]},...,a^{[m]}\} \\ \mathcal R & = \{r^{[1]},r^{[2]},r^{[3]},...,r^{[k]}\} \end{aligned} SAR={s[1],s[2],s[3],...,s[n]}={a[1],a[2],a[3],...,a[m]}={r[1],r[2],r[3],...,r[k]}
这次的重点不在各集合包含的元素，而是随着时间步骤选择各集合元素的过程。根据马尔可夫奖励过程中的逻辑场景回顾中的介绍，对如下场景进行构建：
- 设 t = 0 t = 0 t=0时刻的初始状态为 s 0 s_0 s0；
- 在 s 0 s_0 s0状态下根据当前策略 π ( a ∣ s 0 ) \pi(a \mid s_0) π(a∣s0)中随机选择一个动作 a 0 a_0 a0；
- 在 s 0 , a 0 s_0,a_0 s0,a0确定的条件下，系统根据动作的选择，从当前状态 s 0 s_0 s0转移到下一时刻状态 s 1 s_1 s1,并同时返回一个奖励 r 1 r_1 r1。
我们将 ( s 0 , a 0 , r 1 ) (s_0,a_0,r_1) (s0,a0,r1)称为一个步骤(Step)。 此时，当前时刻 t = 1 t = 1 t=1,当前时刻状态为 s 1 s_1 s1。重复执行上述过程，可以得到如下步骤组成的序列： s 0 , a 0 , r 1 , s 1 , a 1 , r 2 , s 2 , . . . s_0,a_0,r_1,s_1,a_1,r_2,s_2,... s0,a0,r1,s1,a1,r2,s2,... 假设当 t = T t = T t=T时刻，状态 s T s_T sT是终止状态 → \to → T T T时刻达到目标结果。我们称从初始状态 s 0 s_0 s0开始，到达终止状态 s T s_T sT产生的序列： s 0 , a 0 , r 1 , s 1 , a 1 , r 2 , s 2 , . . . , s T − 1 , a T − 1 , r T , s T s_0,a_0,r_1,s_1,a_1,r_2,s_2,...,s_{T-1},a_{T-1},r_T,s_T s0,a0,r1,s1,a1,r2,s2,...,sT−1,aT−1,rT,sT 将该序列称为一个情节/幕。
总结一下，情节必备的两个条件：
- 必然有初始状态；从初始状态开始执行过程。
- 必然有终止状态；一旦智能体达到终止状态，执行过程结束。
从情节的描述来观察，通常情况下，情节不是唯一存在的。
- 因为在执行过程中的任意时刻 t t t，从策略 π ( a ∣ s t ) \pi(a\mid s_t) π(a∣st)中选择的动作 a t a_t at都是随机选择的；
- 并且状态转移过程是系统自身内部产生的结果，这个结果不是智能体干预的信息(马尔可夫奖励过程(MRP))。
因此，不同情节即便都达到了最终状态，但是中间执行过程可能存在差异 → \to → 两个序列可能不同。
但能够确定的是，任意两个情节之间必然是独立同分布的。就像投掷硬币一样，两个情节的产生必然是两次相互独立的试验在相同分布作为前提条件下产生的结果。
相比之下，轨迹(trajectory)就没有终止状态的约束。在轨迹的定义中，智能体即便达到终止状态，依旧可以继续执行过程。因此，一条轨迹中可能包含如下几种情况：
- 轨迹中不包含任何一个情节；
- 轨迹中包含一个/多个情节；
蒙特卡洛方法是通过样本均值逼近表示期望结果的算数均值，因此需要大量采样来计算样本均值；样本数量越多，样本均值结果越稳定。我们如何获取这些样本呢？ 以状态 s s s为例，基于 n n n次采样的蒙特卡洛方法近似求解状态价值函数公式如下： V π ( s ) = E π [ G t ∣ s ∈ S ] ≈ A v e r a g e ( G t ( 1 ) + G t ( 2 ) + . . . + G t ( n ) ∣ s ∈ S ) V_\pi(s) = \mathbb E_{\pi}[G_t\mid s \in \mathcal S] \approx Average(G_t^{(1)} + G_t^{(2)} + ... + G_t^{(n)} \mid s \in \mathcal S) Vπ(s)=Eπ[Gt∣s∈S]≈Average(Gt(1)+Gt(2)+...+Gt(n)∣s∈S) 需要注意的点是， G t ( 1 ) , G t ( 2 ) , . . . , G t ( n ) G_t^{(1)},G_t^{(2)},...,G_t^{(n)} Gt(1),Gt(2),...,Gt(n)是基于 S t = s S_t = s St=s条件下的回报结果。如何得到这些回报呢？
情节的定义中只是约束了它的初始状态和终止状态，我们并没有约束它的路线：
在整个情节经历的过程中，可能存在若干时刻访问了同一个状态，也可能整个情节从开始到结束，也没有访问某个状态。因此，针对同一情节中重复出现相同的状态 s s s，介绍两种访问方法。
-
首次访问型(first-visit)： 在对状态 s s s的价值函数进行估计时，我们可能已经收集了大量的情节。
- 遍历每个情节中的状态，观察是否为状态 s s s；遍历结束后返现该情节中没有状态 s s s,选择其他情节继续遍历；
- 假设在第1个情节中的 t t t时刻首次发现 状态 S t = s S_t = s St=s，计算当前时刻状态的回报如下： G t ( 1 ) ( 1 ) = R t + 1 + γ R t + 2 + . . . + γ T − t − 1 R T G_t^{(1)(1)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T - t-1}R_T Gt(1)(1)=Rt+1+γRt+2+...+γT−t−1RT
记 G t ( 1 ) ( 1 ) G_t^{(1)(1)} Gt(1)(1)为第1个情节中首次发现状态 s s s的回报。并将该结果作为一个样本；与此同时，遍历结束，选择其他情节继续重复执行上述操作； 最终将收集的样本进行统计： V ( s ) = 1 n [ G t ( 1 ) ( 1 ) ( s ) + G t ( 2 ) ( 1 ) ( s ) + . . . + G t ( n ) ( 1 ) ( s ) ] V(s) = \frac{1}{n} [G_t^{(1)(1)}(s) + G_t^{(2)(1)}(s) + ... + G_t^{(n)(1)}(s)] V(s)=n1[Gt(1)(1)(s)+Gt(2)(1)(s)+...+Gt(n)(1)(s)]
-
每次访问型(every-visit)： 和首次访问型的区别在于，在首次发现状态 s s s并计算回报后，继续遍历该情节，直至该情节遍历结束。即在同一情节中重复出现的状态均作为样本使用。 最终收集的样本统计结果如下： V ( s ) = 1 N ( s ) [ G t ( 1 ) ( 1 ) ( s ) + G t ( 1 ) ( 2 ) ( s ) + . . . + G t ( 2 ) ( 1 ) ( s ) + G t ( 2 ) ( 2 ) ( s ) + . . . + G t ( i ) ( j ) ( s ) ] V(s) = \frac{1}{N(s)}[G_t^{(1)(1)}(s) + G_t^{(1)(2)}(s) + ... + G_t^{(2)(1)}(s) + G_t^{(2)(2)}(s) +... + G_t^{(i)(j)}(s)] V(s)=N(s)1[Gt(1)(1)(s)+Gt(1)(2)(s)+...+Gt(2)(1)(s)+Gt(2)(2)(s)+...+Gt(i)(j)(s)]
首次访问型(first-visit)和每次访问型(every-visit)相比之下各有利弊： 首次访问型的优势与每次访问型的劣势：
- 由于 情节与情节之间相互独立，若从每个相互独立的情节中取出唯一一个状态 s s s的回报 → \to → 首次访问型产生的回报样本同样也是经过独立试验产生的 相互独立的样本。
- 相比之下，若将相同情节下的状态 s s s的回报均作为样本，根据回报的计算过程，回报之间可能存在关联关系(一定存在某一时刻同样是状态 s s s的回报 G t + i G_{t+i} Gt+i和 G t ( 1 ) ( 1 ) ( s ) G_t^{(1)(1)}(s) Gt(1)(1)(s)之间满足如下关系)： G t ( 1 ) ( 1 ) ( s ) = R t + 1 + γ ∗ R t + 2 + . . . + γ T − t − 1 R T = R t + 1 + γ ∗ G t + 1 = R t + 1 + γ ∗ R t + 2 + γ 2 G t + 2 = R t + 1 + γ ∗ R t + 2 + . . . + γ i G t + i \begin{aligned} G_t^{(1)(1)}(s) & = R_{t+1} + \gamma * R_{t+2} + ... + \gamma^{T - t-1}R_T\\ & = R_{t+1} + \gamma * G_{t+1} \\ & = R_{t+1} + \gamma * R_{t+2} + \gamma^2 G_{t+2}\\ & = R_{t+1} + \gamma * R_{t+2} + ... + \gamma^i G_{t+i}\\ \end{aligned} Gt(1)(1)(s)=Rt+1+γ∗Rt+2+...+γT−t−1RT=Rt+1+γ∗Gt+1=Rt+1+γ∗Rt+2+γ2Gt+2=Rt+1+γ∗Rt+2+...+γiGt+i
首次访问型的劣势与每次访问型的优势：
- 由于首次访问型只从一个情节中获取一个样本(在情节中存在状态 s s s的条件下)，因此获取样本集需要的情节数量 ≥ \geq ≥ 样本集数量(可能存在某个情节中不含状态 s s s)。
- 相比之下，每次访问型可能仅需要更少的情节数量就可以得到足够多的样本。因此，从收集样本花费代价的角度观察，每次访问型优于首次访问型。
这里以首次访问型为例，具体算法如下：
输入待评估的随机策略： π ( a ∣ s ) \pi(a \mid s) π(a∣s)初始化操作(Initialization operation)1. 对 ∀ s ∈ S \forall s \in \mathcal S ∀s∈S,初始化 V ( s ) ∈ R V(s) \in\mathbb R V(s)∈R； 2.状态 s s s被统计次数 c o u n t ( s ) = 0 count(s) = 0 count(s)=0算法过程(Algorithmic Process)1. repeat 对每一个情节： k = 0 , 1 , 2 , . . . k=0,1,2,... k=0,1,2,... 2. 根据策略 π ( a ∣ s ) \pi(a \mid s) π(a∣s),生成一个情节序列：{ S 0 , A 0 , R 1 , S 1 , A 1 , R 2 , . . . , S T − 1 , A T − 1 , R T , S T S_0,A_0,R_1,S_1,A_1,R_2,...,S_{T-1},A_{T-1},R_T,S_T S0,A0,R1,S1,A1,R2,...,ST−1,AT−1,RT,ST} 3. for 情节中的每一步(时刻) t = T − 1 → 0 t = T - 1 \to 0 t=T−1→0 do： 4. G ← γ G + R t + 1 G \gets\gamma G + R_{t+1} G←γG+Rt+1 5. if S t ∉ { S 0 , S 1 , . . . , S t − 1 } S_t \notin \{S_0,S_1,...,S_{t-1}\} St∈/{S0,S1,...,St−1} then 6. c o u n t ( S t ) ← c o u n t ( S t ) + 1 count(S_t) \gets count(S_t) + 1 count(St)←count(St)+1 7. V ( S t ) ← V ( S t ) + 1 c o u n t ( S t ) ( G − V ( S t ) ) V(S_t) \gets V(S_t) + \frac{1}{count(S_t)}(G - V(S_t)) V(St)←V(St)+count(St)1(G−V(St))8. end if9. end for输出结果 V ( S t ) V(S_t) V(St)由于
{
S
0
,
A
0
,
R
1
,
S
1
,
A
1
,
R
2
,
.
.
.
,
S
T
−
1
,
A
T
−
1
,
R
T
,
S
T
}
\{S_0,A_0,R_1,S_1,A_1,R_2,...,S_{T-1},A_{T-1},R_T,S_T\}
{S0,A0,R1,S1,A1,R2,...,ST−1,AT−1,RT,ST}都是已知信息，因此为了简化运算,算法中选择从
T
−
1
T-1
T−1时刻开始向前遍历，只要发现
S
t
S_t
St,即可停止遍历，并进行下一个情节的遍历计算。 这里均值计算使用增量更新方式进行求解。能够很好地观察遍历过程中价值函数的变化，并且在每次迭代一个情节时，
V
(
S
t
)
V(S_t)
V(St)都会更新一次结果。 这里的反向遍历 -> 简化运算的思路简单说明一下 如果是正向遍历
→
\to
→ 要执行的运算次数：
k
→
0
:
G
0
=
R
1
+
γ
R
2
+
γ
2
R
3
+
.
.
.
+
γ
T
−
1
R
T
k
→
1
:
G
1
=
R
2
+
γ
R
3
+
γ
2
R
4
+
.
.
.
+
γ
T
−
1
R
T
k
→
2
:
G
2
=
R
3
+
γ
R
4
+
γ
2
R
5
+
.
.
.
+
γ
T
−
1
R
T
.
.
.
\begin{aligned} k \to 0 : G_0 & = R_1 + \gamma R_2 + \gamma^2 R_3 + ... + \gamma^{T-1}R_T \\ k \to 1 :G_1 & = R_2 + \gamma R_3 + \gamma^2 R_4 + ... + \gamma^{T-1}R_T \\ k \to 2 :G_2 & = R_3 + \gamma R_4 + \gamma^2 R_5 + ... + \gamma^{T-1}R_T \\ ... \end{aligned}
k→0:G0k→1:G1k→2:G2...=R1+γR2+γ2R3+...+γT−1RT=R2+γR3+γ2R4+...+γT−1RT=R3+γR4+γ2R5+...+γT−1RT (乘法暂时忽略)第一次需要计算
T
−
1
T-1
T−1次加法；第二次要计算
T
−
2
T-2
T−2次加法；…以此类推； 如果是反向遍历
→
\to
→ 要执行的运算次数：
k
→
T
−
1
:
G
T
−
1
=
R
T
−
1
+
γ
R
T
k
→
T
−
2
:
G
T
−
2
=
R
T
−
2
+
γ
R
T
−
1
+
γ
2
R
T
k
→
T
−
3
:
G
T
−
3
=
R
T
−
3
+
γ
R
T
−
2
+
γ
2
R
T
−
1
+
γ
3
R
T
.
.
.
\begin{aligned} k \to T- 1 : G_{T-1} & = R_{T-1} + \gamma R_T \\ k \to T- 2:G_{T-2} & = R_{T-2} + \gamma R_{T-1} + \gamma^2 R_T \\ k \to T-3 :G_{T-3} & = R_{T-3} + \gamma R_{T-2} + \gamma^2 R_{T-1} + \gamma^3R_T \\ ... \end{aligned}
k→T−1:GT−1k→T−2:GT−2k→T−3:GT−3...=RT−1+γRT=RT−2+γRT−1+γ2RT=RT−3+γRT−2+γ2RT−1+γ3RT (乘法暂时忽略)第一次需要计算1次加法；第二次要计算2次加法；…以此类推； 假设都在
t
t
t次循环后找到了状态
s
s
s： 正向遍历需要计算加法的次数：
∑
i
=
1
t
T
−
i
=
t
×
T
−
1
2
t
(
t
+
1
)
\sum_{i=1}^tT -i = t\times T - \frac{1}{2}t(t+1)
i=1∑tT−i=t×T−21t(t+1) 反向遍历需要计算加法的次数：
∑
i
=
1
t
i
=
1
2
t
(
t
+
1
)
\sum_{i=1}^ti = \frac{1}{2}t(t+1)
i=1∑ti=21t(t+1) 一般情况下，情节序列的长度是较大的(随便几步就找到最优解了，还要强化学习干什么)，因此：
∑
i
=
1
t
T
−
i
≥
∑
i
=
1
t
i
(
T
=
t
+
1
取
等
)
\sum_{i=1}^t T-i \geq \sum_{i=1}^ti(T=t+1取等)
i=1∑tT−i≥i=1∑ti(T=t+1取等)
无论是首次访问型还是每次访问型，它的存储方式都可以用哈希表的方式进行存储(画的草率，见谅哈)。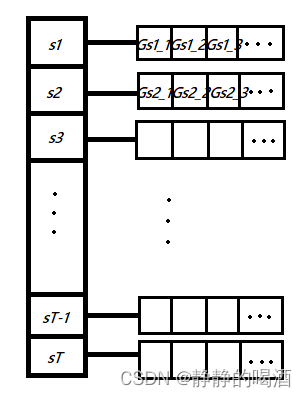 
以每次型访问为例，对每个步骤的迭代必然会在表中添加一个回报元素。
下一节将介绍基于状态-动作价值函数的蒙特卡洛方法求解。 相关参考： 【强化学习】蒙特卡洛方法-策略评估 深度强化学习原理、算法pytorch实战 —— 刘全，黄志刚编著
