策略梯度方法介绍——Value-Based强化学习方法 VS Policy-Based强化学习方法

目录

从本节开始，将介绍策略梯度方法求解强化学习任务。

回顾：基于价值函数(Value-Based)的强化学习方法 Value-Based强化学习方法介绍

从前面介绍的各种求解强化学习任务的方法中，总共介绍了3大类求解 马尔可夫决策过程(Markov Decision Process,MDP)问题的方法，它们分别是：

• 动态规划方法(Dynamic Programming,DP)；
• 蒙特卡洛方法(Monte Carlo,MC)；
• 时序差分方法(Temporal-Difference,TD)

这三种方法存在共同特点：

• 在求解强化学习任务时，最终目标是求解满足规则的最优策略 π \pi π。 但以上三种方法并没有 直接求解 策略 π \pi π这个变量，而是先计算 状态价值函数 V π ( s ) V_\pi(s) Vπ​(s) / 状态-动作价值函数 q π ( s , a ) q_\pi(s,a) qπ​(s,a)；然后再基于价值函数结果改进 策略 π \pi π，从而实现策略 π \pi π的迭代更新。
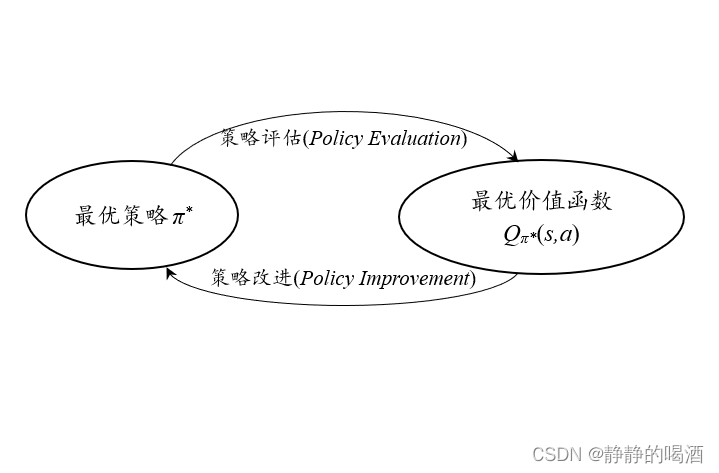
• 无论是动态规划方法的策略迭代，还是蒙特卡洛控制、时序差分控制，它们呈现的共同点都是在策略改进过程中，均选择最优价值函数对应的动作作为新的策略。 (即便在同轨策略方法中存在使用 ϵ − \epsilon- ϵ−贪心策略修正的情况，但并不影响 选择“最优动作”作为新的策略 的本质） a ∗ = π ′ ( s ) = arg ⁡ max ⁡ a q π ( s , a ) a^* = \pi'(s) = \mathop{\arg\max}\limits_{a}q_\pi(s,a) a∗=π′(s)=aargmax​qπ​(s,a)
• 这三种方法都是 表格式强化学习 的代表方法，其主要思想是：

1. 在算法开始前，初始化一个存储价值函数的空间 Q − T a b l e Q-Table Q−Table；
2. 在迭代过程中，每次迭代更新对应位置 ( s t a t e , a c t i o n ) (state,action) (state,action)的价值函数信息；
3. 并不是从迭代开始就会将正确的信息加入到 Q − T a b l e Q-Table Q−Table中(Q-Learning中产生的就最大化偏差是个很好的例子)，而是通过不断试错——与环境不断交互并从环境的反馈信息中进行学习。

Value-Based强化学习方法的缺陷

什么样的情况是Value-Based强化学习方法 无法解决/解决不好 的呢？

• 根据上面的特点介绍，我们发现，每次策略改进得到的最优策略 π ∗ \pi^* π∗一定是 确定性策略/基于 ϵ − \epsilon- ϵ−贪心策略修正后的 软性策略。 但ϵ-贪心策略仍然改变不了‘最优动作占据新策略最多权重，并且远超其他动作权重’的本质。因此，该策略主体仍然是某一确定性动作，即价值函数最高结果对应的动作。

  但是每次迭代产生的这种确定性动作反而限制了迭代过程(这样会导致每次迭代更新的 方向性极强)。在真实环境中，我们更想要一个随机性策略而不是确定性动作。 这里说的‘随机性策略’和‘软性策略’截然不同，因为‘软性策略中的随机性’是人为定的超参数(ϵ),而不是机器生成的;

• Value-Based强化学习方法面对的问题一般情况下状态(State)、动作(Action) 等变量是 可数的、有穷的 ：前面介绍具体强化学习方法时，经常对 状态集合 S \mathcal S S,动作集合 A \mathcal A A,奖励集合 R \mathcal R R进行 逻辑场景构建：传送门 S = { s 1 , s 2 , ⋯   , s m } A = { a 1 , a 2 , ⋯   , a n } R = { r 1 , r 2 , ⋯   , r k } \mathcal S = \{s_1,s_2,\cdots,s_m\} \\ \mathcal A = \{a_1,a_2,\cdots,a_n\} \\ \mathcal R = \{r_1,r_2,\cdots,r_k\} S={s1​,s2​,⋯,sm​}A={a1​,a2​,⋯,an​}R={r1​,r2​,⋯,rk​} 并且在构建时声明它们是 离散型随机变量。但是在真实环境中，我们遇到的动作(Action) 不一定是离散的：

  示例：二维平面内智能体运动方向 a a a的选择 如果使用角度来描述它的运动方向(智能体选择的运动方向 与 当前状态智能体运动方向 之间的夹角)：那么有效的运动方向范围表示如下： a ∈ [ 0 , 2 π ] a \in [0,2\pi] a∈[0,2π] 如果将运动方向的选择看成智能体选择的动作，即动作的选择结果在 [ 0 , 2 π ] [0,2\pi] [0,2π]内均有效——该场景中的动作明显是一个连续型随机变量，没有办法将 [ 0 , 2 π ] [0,2\pi] [0,2π]内 所有动作 全部列举出来。

• 针对步骤2若后退一步——假设我们动作的选择是可数的、有穷的，但是动作的数量 极多，使用价值函数强化学习方法进行求解时，我们需要建立一个超级大的 Q − T a b l e → Q-Table \to Q−Table→ 用于迭代过程中价值函数的更新。但这种操作内存占用情况是非常严重的。

综上，Value-Based强化学习方法并不能有效解决上述问题。

基于策略(Policy-Based)的强化学习方法 适用场景

相比于Value-Based强化学习方法，Policy-Based强化学习方法不再利用价值函数，而是利用 策略函数 直接选择动作。

对比Value-Based强化学习方法的缺陷，我们介绍Policy-Based强化学习方法适用的场景：

• 产生的策略是随机性策略；
• 动作是连续型随机变量(动作空间连续)；

这相比仅仅是针对确定性策略、动作是离散型随机变量的Value-Based强化学习方法，Policy-Based强化学习方法能够解决问题的范围 更加广泛——使用Policy-Based强化学习方法同样可以求解Value-Based强化学习方法的场景。

求解过程

在Value-Based强化学习方法中，策略 π ( a ∣ s ) \pi(a \mid s) π(a∣s)指的是给定状态 s s s条件下，有意义的动作 a a a的概率分布，其数学符号表示如下： π ( a ∣ s ) = ( π ( a 1 ∣ s ) π ( a 2 ∣ s ) ⋮ π ( a N ∣ s ) ) ( a 1 , a 2 , ⋯   , a N ∈ A ( s ) ) \begin{aligned} \pi(a \mid s) = \begin{pmatrix} \pi(a_1 \mid s) \\ \pi(a_2 \mid s) \\ \vdots \\ \pi(a_N \mid s) \\ \end{pmatrix}(a_1,a_2,\cdots,a_N \in \mathcal A(s)) \end{aligned} π(a∣s)=⎝ ⎛​π(a1​∣s)π(a2​∣s)⋮π(aN​∣s)​⎠ ⎞​(a1​,a2​,⋯,aN​∈A(s))​ 但Policy-Based强化学习方法中的动作 a a a是连续性随机变量，因此此时的策略 π \pi π不再是上述概率集合的形式，而是可微函数的形式——动作发生的概率受到某个概率密度函数的控制。

根据上述思路，进行如下分析：

• 根据实际情况，假设动作 a a a服从某一概率密度函数 P ( a ∣ s ; θ ) P(a\mid s;\theta) P(a∣s;θ)(换种思路理解——将动作 a a a理解成从概率模型 P ( a ∣ s ; θ ) P(a\mid s;\theta) P(a∣s;θ)产生的样本) 其中s表示给定的状态，theta表示概率密度函数的参数信息。
• 最终目标从求解 π ( a ∣ s ) \pi(a \mid s) π(a∣s)转换成求解策略中的参数 θ \theta θ。 因此，将含参数 θ \theta θ的策略称为策略函数。记作 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ),通常情况下可简写成 π θ \pi_{\theta} πθ​。 π ( a ∣ s ; θ ) = P ( A t = a ∣ S t = s , θ t = θ ) \pi(a \mid s;\theta) = P(A_t = a \mid S_t = s,\theta_t = \theta) π(a∣s;θ)=P(At​=a∣St​=s,θt​=θ) 关于策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)分布的特点，上面我们提到，使用Policy-Based强化学习方法同样可以求解Value-Based强化学习方法的场景，那么动作分别是离散和连续的情况下， π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)是如何进行表示的？

1. 如果动作 a a a是离散型随机变量 → \to → 使用   s o f t m a x \ softmax  softmax函数将其映射为 指数族分布： 这里并不是一定要使用softmax函数进行映射 -> 只要能够映射为‘指数族分布’即可。 将 h ( s , a ; θ ) h(s,a;\theta) h(s,a;θ)函数定义为‘动作偏好值’ -> 将离散型的策略 π ( a ∣ s ) \pi(a \mid s) π(a∣s)视为关于 θ \theta θ的一个函数，仅此而已; π ( a ∣ s ) → e h ( s , a ; θ ) ∑ k ∈ A ( s ) e h ( s , k ; θ ) \pi(a \mid s) \to \frac{e^{h(s,a;\theta)}}{\sum_{k \in \mathcal A(s)} e^{h(s,k;\theta)}} π(a∣s)→∑k∈A(s)​eh(s,k;θ)eh(s,a;θ)​
2. 如果动作 a a a是连续型随机变量 → a \to a →a服从分布的复杂性有很多种，这里不妨设 a a a服从 高斯分布 ： 这里将高斯分布中的 μ , σ \mu,\sigma μ,σ看作参数 θ \theta θ的函数，若 θ \theta θ能够求解， μ , σ \mu,\sigma μ,σ同样也可以被求解，最终求解整个分布。 s是状态，s是给定的。 μ = μ ( s ; θ ) , σ = σ ( s ; θ ) \mu = \mu(s;\theta),\sigma = \sigma(s;\theta) μ=μ(s;θ),σ=σ(s;θ) 至此，假设 a a a是服从1维随机变量的高斯分布，策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)表示如下： π ( a ∣ s ; θ ) → 1 2 π σ ( s ; θ ) exp ⁡ { − ( a − μ ( s ; θ ) ) 2 2 σ 2 ( s ; θ ) } \pi(a \mid s;\theta) \to \frac{1}{\sqrt{2\pi}\sigma(s;\theta)}\exp\{{-\frac{(a - \mu(s;\theta))^2}{2\sigma^2(s;\theta)}}\} π(a∣s;θ)→2π ​σ(s;θ)1​exp{−2σ2(s;θ)(a−μ(s;θ))2​}

• 为了衡量策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)的优劣性 → \to → 围绕参数 θ \theta θ构建一个目标函数 J ( θ ) \mathcal J(\theta) J(θ)。通常情况下，最直接的思路就是将 J ( θ ) \mathcal J(\theta) J(θ)定义为情节中初始状态回报(Return)的期望，即 初始状态的状态价值函数 V π ( a ∣ s ; θ ) ( s 0 ) V_{\pi(a |s;\theta)}(s_0) Vπ(a∣s;θ)​(s0​)。 '目标函数'并不是Policy-Based强化学习方法的特有概念，在Value-Based强化学习方法中也存在‘目标函数’的说法： V π ( s ) , q π ( s , a ) V_\pi(s),q_\pi(s,a) Vπ​(s),qπ​(s,a)都是目标函数; 之所以选择‘初始状态’回报的期望 -> 极大限度地将 R 1 , R 2 , ⋯   , R T R_1,R_2,\cdots,R_T R1​,R2​,⋯,RT​利用上。 数学符号表示如下： J ( θ ) = V π ( a ∣ s ; θ ) ( s 0 ) = E π ( a ∣ s ; θ ) [ G 0 ] = E π ( a ∣ s ; θ ) [ R 1 + γ R 2 + ⋯ + γ T − 1 R T ] \begin{aligned} \mathcal J(\theta) & = V_{\pi(a \mid s;\theta)}(s_0) \\ & = \mathbb E_{\pi(a \mid s;\theta)}[G_0] \\ & = \mathbb E_{\pi(a \mid s;\theta)}[R_1 + \gamma R_2 + \cdots + \gamma^{T-1}R_T] \end{aligned} J(θ)​=Vπ(a∣s;θ)​(s0​)=Eπ(a∣s;θ)​[G0​]=Eπ(a∣s;θ)​[R1​+γR2​+⋯+γT−1RT​]​

至此，我们推演一下策略梯度方法的求解过程：

• 初始参数 θ i n i t \theta_{init} θinit​，基于该参数得到初始策略函数 π ( a ∣ s ; θ i n i t ) \pi(a \mid s;\theta_{init}) π(a∣s;θinit​)； θ i n i t → π ( a ∣ s ; θ i n i t ) \theta_{init} \to \pi(a \mid s;\theta_{init}) θinit​→π(a∣s;θinit​)
• 基于该策略函数去执行一个完整情节 { S 0 , a 0 , S 1 , a 1 , ⋯   , S T − 1 , a T − 1 , S T } \{S_0,a_0,S_1,a_1,\cdots,S_{T-1},a_{T-1},S_T\} {S0​,a0​,S1​,a1​,⋯,ST−1​,aT−1​,ST​},得到奖励结果如下： R 1 , R 2 , ⋯   , R T R_1,R_2,\cdots,R_{T} R1​,R2​,⋯,RT​
• 基于奖励结果 → \to → 求解目标函数 J ( θ i n i t ) \mathcal J(\theta_{init}) J(θinit​); J ( θ i n i t ) = E π ( a ∣ s ; θ ) [ R 1 + γ R 2 + ⋯ + γ T − 1 R T ] \mathcal J(\theta_{init}) = \mathbb E_{\pi(a \mid s;\theta)}[R_1 + \gamma R_2 + \cdots + \gamma^{T-1}R_T] J(θinit​)=Eπ(a∣s;θ)​[R1​+γR2​+⋯+γT−1RT​]
• 从常规 机器学习的梯度方法 思考，对 J ( θ i n i t ) \mathcal J(\theta_{init}) J(θinit​)求解 梯度，再配合学习率 α \alpha α对 θ i n i t \theta_{init} θinit​进行更新； 由于 J ( θ i n i t ) \mathcal J(\theta_{init}) J(θinit​)是初始状态的状态价值函数，自然是希望 J ( θ i n i t ) \mathcal J(\theta_{init}) J(θinit​)越大越好，因此，这里使用 梯度上升法 对 θ \theta θ进行迭代： 该步骤在后续进行讲解。 θ ′ ← θ i n i t + α ∇ J ( θ i n i t ) \theta' \gets \theta_{init} + \alpha \nabla \mathcal J(\theta_{init}) θ′←θinit​+α∇J(θinit​)
• 此时，得到一个更新后的新参数 θ ′ \theta' θ′，将 θ ′ ← θ i n i t \theta' \gets \theta_{init} θ′←θinit​重新执行上述步骤，直至 J ( θ ) \mathcal J(\theta) J(θ)达到最优并且稳定为止。

但上述推演过程中我们漏掉了一个问题：如何求解梯度 ∇ J ( θ i n i t ) \nabla\mathcal J(\theta_{init}) ∇J(θinit​)？

关于梯度 ∇ J ( θ ) \nabla\mathcal J(\theta) ∇J(θ)变化的核心要素——状态分布 状态分布思路的产生

基于上一节的思路继续思考：到底是哪些要素影响梯度 ∇ J ( θ ) \nabla\mathcal J(\theta) ∇J(θ)的变化？

首先观察 ∇ J ( θ ) \nabla\mathcal J(\theta) ∇J(θ)和 θ \theta θ之间的关联关系。 为了简化计算： → \to → 不妨假定动作 a a a服从1维随机变量的某种分布； → \to → 此时参数 θ \theta θ同样也是1维随机变量； → \to → 导致求解梯度 ∇ J ( θ ) \nabla\mathcal J(\theta) ∇J(θ)退化成对 J ( θ ) \mathcal J(\theta) J(θ)的导数计算 J ′ ( θ ) \mathcal J'(\theta) J′(θ)；

从导数定义角度观察 J ′ ( θ ) \mathcal J'(\theta) J′(θ)： J ′ ( θ ) = lim ⁡ Δ θ → 0 Δ J ( θ ) Δ θ \mathcal J'(\theta) = \mathop{\lim}\limits_{\Delta\theta\to 0}\frac{\Delta \mathcal J(\theta)}{\Delta \theta} J′(θ)=Δθ→0lim​ΔθΔJ(θ)​

继续观察：如果参数 θ \theta θ发生变化( Δ θ \Delta \theta Δθ)，到底如何影响 J ( θ ) \mathcal J(\theta) J(θ)跟着发生变化( Δ J ( θ ) \Delta \mathcal J(\theta) ΔJ(θ))?

• (必然发生的情况)首先，由于 θ \theta θ是策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)的参数，因此 θ \theta θ的变化必然引起策略参数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)的变化；

  策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)的变化，自然会引发 J ( θ ) \mathcal J(\theta) J(θ)的变化； J ( θ ) = E π ( a ∣ s ; θ ) [ R 1 + γ R 2 + ⋯ + γ T − 1 R T ] \mathcal J(\theta) = \mathbb E_{\pi(a \mid s;\theta)}[R_1 + \gamma R_2 + \cdots + \gamma^{T-1}R_T] J(θ)=Eπ(a∣s;θ)​[R1​+γR2​+⋯+γT−1RT​]

• (状态分布产生的核心思路)基于策略函数产生的一条完整情节，那么该情节中 状态出现的概率分布和策略函数之间存在直接联系。具体描述如下：

  基于参数 θ \theta θ产生的策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)，并使用该策略执行了一个完整情节。该情节中的状态部分表示如下： { s 0 , s 1 , s 2 , ⋯   , s T } \{s_0,s_1,s_2,\cdots,s_T\} {s0​,s1​,s2​,⋯,sT​}

  其中 s T s_T sT​表示终结状态。如果状态(State)自身是离散型随机变量，状态集合 S \mathcal S S表示如下： S = { s ( 0 ) , s ( 1 ) , ⋯   , s ( N ) } \mathcal S = \{s^{(0)},s^{(1)},\cdots,s^{(N)}\} S={s(0),s(1),⋯,s(N)} 在完整情节中，各随机变量在情节种出现的次数(频率)和概率表示如下：

  s ( 0 ) s^{(0)} s(0) s ( 1 ) s^{(1)} s(1) s ( 2 ) s^{(2)} s(2) ⋯ \cdots ⋯ s ( N ) s^{(N)} s(N)出现次数 k 0 k_0 k0​ k 1 k_1 k1​ k 2 k_2 k2​ ⋯ \cdots ⋯ k N k_N kN​出现概率 k 0 T \frac{k_0}{T} Tk0​​ k 1 T \frac{k_1}{T} Tk1​​ k 2 T \frac{k_2}{T} Tk2​​ ⋯ \cdots ⋯ k N T \frac{k_N}{T} TkN​​

  ∑ i = 1 N k i = T \sum_{i=1}^N k_i = T i=1∑N​ki​=T 至此，我们得到了一组关于状态的概率分布： p ( s ) = [ k 0 T , k 1 T , ⋯   , k N T ] p(s) = [\frac{k_0}{T},\frac{k_1}{T},\cdots,\frac{k_N}{T}] p(s)=[Tk0​​,Tk1​​,⋯,TkN​​] 我们在机器学习笔记——极大似然估计与最大后验概率估计介绍过 频率学派角度看待机器学习问题，并引用了黑格尔的一句名言：存在即合理。

  虽然产生的状态分布 p ( s ) p(s) p(s)和策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)之间 不是映射关系：

  • 因为策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)是随机性策略，虽然知道动作对应的概率分布，但该状态选择的具体动作是未知的；
  • 状态转移过程 P ( s ′ , r ∣ s , a ) P(s',r \mid s,a) P(s′,r∣s,a)同样也是一个概率分布，并且状态转移过程是系统内部发生的变化，和智能体的主观意志无关；

  但是根据频率学派角度的观点： p ( s ) p(s) p(s)是通过策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)产生出来的【真实存在】的样本，既然能够产生，自然存在它的合理性。

  因此，状态分布指向的结果即：情节中 策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)的变化会影响 状态分布的变化 ，而状态分布的变化会影响目标函数 J ( θ ) \mathcal J(\theta) J(θ)的变化。

状态分布的求解过程

上面介绍了相同的策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)可能得到各种各样状态分布样本(非映射关系)；但是我们需要对这些样本的特征进行归纳——归纳后的结果与策略函数之间存在具体关系。

这里引入两个新的概念：

• 平均次数(与表格中的“出现次数”对应)，平均次数定义可以表述为：以某一具体状态 s s s在某完整情节中出现的期望次数。数学符号表示为 η ( s ) \eta(s) η(s)；
• 出现概率(与表格中的“出现概率”对应)，具体表述为状态 s s s的平均次数和所有状态的平均次数的比值。数学符号表示为 μ ( s ) \mu(s) μ(s)；

如何求解 η ( s ) \eta(s) η(s)？我们将 η ( s ) \eta(s) η(s)的求解过程分为两个部分：

• 状态 s s s是初始状态 → \to → 状态 s s s没有前继状态； 根据概率的频率定义，状态 s s s在初始状态出现的平均次数即 重复大量试验后，状态 s s s是初始状态的频率，即 s s s被选择的概率。 → \to → 使用 h ( s ) h(s) h(s)表示 s s s被选择的概率。

• 状态 s s s是非初始状态 → \to → 状态 s s s在情节中必然存在一个前继状态通过状态转移的方式 得到状态 s s s。令前继状态为 s ˉ \bar s sˉ；

  根据该思路继续思考：

  • 如果知道了状态 s s s所有可能的前继状态 s ˉ \bar s sˉ的平均次数 η ( s ˉ ) \eta(\bar s) η(sˉ)；
  • 并且知道在前继状态 s ˉ \bar s sˉ条件下，动作 a a a的概率分布 π ( a ∣ s ˉ ) \pi(a \mid \bar s) π(a∣sˉ)；
  • 并且还知道每个前继续状态 s ˉ \bar s sˉ转移到状态 s s s的转移概率 P ( s ∣ s ˉ , a ) P(s \mid \bar s,a) P(s∣sˉ,a)；

  那么可以求解期望的方式求解状态 s s s的平均次数： ∑ s ˉ η ( s ˉ ) ∑ a ∈ A ( s ˉ ) π ( a ∣ s ˉ ) P ( s ∣ s ˉ , a ) \sum_{\bar s}\eta(\bar s)\sum_{a \in \mathcal A(\bar s)} \pi(a \mid \bar s)P(s \mid \bar s,a) sˉ∑​η(sˉ)a∈A(sˉ)∑​π(a∣sˉ)P(s∣sˉ,a)

• 将上述两种状态(初始状态\非初始状态)结果相加，则有： η ( s ) = h ( s ) + ∑ s ˉ η ( s ˉ ) ∑ a ∈ A ( s ˉ ) π ( a ∣ s ˉ ) P ( s ∣ s ˉ , a ) \eta(s) = h(s) + \sum_{\bar s}\eta(\bar s)\sum_{a \in \mathcal A(\bar s)} \pi(a \mid \bar s)P(s \mid \bar s,a) η(s)=h(s)+sˉ∑​η(sˉ)a∈A(sˉ)∑​π(a∣sˉ)P(s∣sˉ,a) 我们发现，上述式子是个迭代式子——它描述了状态 s s s的平均次数 η ( s ) \eta(s) η(s)与它前继状态的平均次数 η ( s ˉ ) \eta(\bar s) η(sˉ)的 关联关系。 在求解 η ( s ˉ ) \eta(\bar s) η(sˉ)时，也会使用上式与 s ˉ \bar s sˉ的前继构建关联关系。 以此类推，必然会递推到初始状态；

  因此，构建新的数学符号对上式进行修改，修改结果如下： η ( s ) = ∑ k = 0 T − 1 P r { s 0 → s , k , π } \begin{aligned} \eta(s) & = \sum_{k=0}^{T-1}P_r\{s_0 \to s,k,\pi\} \end{aligned} η(s)​=k=0∑T−1​Pr​{s0​→s,k,π}​ 该式可以理解为：

  • P r { s 0 → s , k , π } → P_r\{s_0 \to s,k,\pi\} \to Pr​{s0​→s,k,π}→ 初始状态 s 0 s_0 s0​，在策略函数 π \pi π的条件下，进行了 k k k次状态转移，最终达到状态 s s s的概率；
  • 在得到上述概率后，相当于有 P r { s 0 → s , k , π } P_r\{s_0 \to s,k,\pi\} Pr​{s0​→s,k,π}的概率必然在对应位置出现1次状态 s s s，那么状态 s s s在该位置出现的平均次数即： P r { s 0 → s , k , π } × 1 P_r\{s_0 \to s,k,\pi\} \times 1 Pr​{s0​→s,k,π}×1 那么状态 s s s在整个情节中出现的平均次数即： ∑ k = 0 T − 1 P r { s 0 → s , k , π } × 1 = ∑ k = 0 T − 1 P r { s 0 → s , k , π } \sum_{k=0}^{T-1}P_r\{s_0 \to s,k,\pi\} \times 1 = \sum_{k=0}^{T-1}P_r\{s_0 \to s,k,\pi\} k=0∑T−1​Pr​{s0​→s,k,π}×1=k=0∑T−1​Pr​{s0​→s,k,π}

出现概率 μ ( s ) \mu(s) μ(s)根据概念描述即：某一状态的平均次数占所有状态平均次数的比重。 μ ( s ) = η ( s ) ∑ s ′ η ( s ′ ) \mu(s) = \frac{\eta(s)}{\sum_{s'}\eta(s')} μ(s)=∑s′​η(s′)η(s)​

状态分布的求解全部结束，下一节将介绍策略梯度定理。

相关参考： 【强化学习】策略梯度方法-策略近似 深度强化学习原理、算法pytorch实战 —— 刘全，黄志刚编著