策略梯度方法介绍——带基线的REINFORCE

引言

上一节介绍了蒙特卡洛策略梯度方法(REINFORCE)的推导过程，本节将介绍REINFORCE的一种优化方式——基于baseline的REINFORCE方法。

回顾：REINFORCE算法

使用策略梯度定理表示目标函数的梯度 ∇ J ( θ ) \nabla \mathcal J(\theta) ∇J(θ)如下： ∇ J ( θ ) = E S t ∼ ρ π θ ; A t ∼ π θ [ ∇ log ⁡ π ( A t ∣ S t ; θ ) G t ] \nabla \mathcal J(\theta) = \mathbb E_{S_t \sim \rho^{\pi_{\theta}};A_t \sim \pi_{\theta}}[\nabla \log \pi(A_t \mid S_t;\theta)G_t] ∇J(θ)=ESt​∼ρπθ​;At​∼πθ​​[∇logπ(At​∣St​;θ)Gt​] 并基于这种期望表示，使用蒙特卡洛方法通过样本均值的方式近似求解 ∇ J ( θ ) \nabla \mathcal J(\theta) ∇J(θ)；最终对策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)中的参数 θ \theta θ进行 增量更新： θ t + 1 = θ t + α ∇ log ⁡ π ( A t ∣ S t ; θ ) G t \theta_{t+1} = \theta_t + \alpha \nabla \log \pi(A_t \mid S_t;\theta)G_t θt+1​=θt​+α∇logπ(At​∣St​;θ)Gt​

REINFORCE方法在执行过程中的问题

上述的采样操作确实实现了对 ∇ J ( θ ) \nabla \mathcal J(\theta) ∇J(θ)的 无偏估计，但在真实环境中，假设执行每个动作的奖励(Reward)均为正：从而使对应状态的回报(Return)恒为正值： G t = R t + 1 + γ R t + 2 + ⋯ + γ T − 1 R T ≥ 0 G_t = R_{t+1} +\gamma R_{t+2} + \cdots + \gamma^{T-1} R_T \geq 0 Gt​=Rt+1​+γRt+2​+⋯+γT−1RT​≥0 从而导致 ∇ J ( θ ) \nabla \mathcal J(\theta) ∇J(θ)结果大于等于0恒成立 → \to → θ \theta θ在增量更新中的采集样本大于等于0恒成立，策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)中的 θ \theta θ不断增长： ∇ log ⁡ π ( A t ∣ S t ; θ ) G t ≥ 0 θ t + 1 = θ t + α ∇ log ⁡ π ( A t ∣ S t ; θ ) G t ↑ \nabla \log \pi (A_t \mid S_t;\theta)G_t \geq 0 \\ \theta_{t+1} = \theta_t + \alpha \nabla \log \pi(A_t \mid S_t;\theta)G_t \uparrow ∇logπ(At​∣St​;θ)Gt​≥0θt+1​=θt​+α∇logπ(At​∣St​;θ)Gt​↑ 导致这种情况会导致策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)(可以理解成 关于 θ \theta θ的概率密度函数) 由于 θ \theta θ的不断增加而出现 每个动作被选择的概率存在不同程度地提升。 这一现象会严重降低学习速率，导致梯度方差的增大 → \to → 即存在 动作大概率只能从若干个有限范围内局部选择 的现象。

带基线的REINFORCE

基于上述问题，为了降低蒙特卡洛方法引起的梯度方差较高的现象，有这样一种思路：

• 基于方差和期望之间的关系： V a r ( X ) = E [ X 2 ] − { E [ X ] } 2 Var(X) = \mathbb E[X^2] - \{\mathbb E[X]\}^2 Var(X)=E[X2]−{E[X]}2 如果将 E [ X 2 ] \mathbb E[X^2] E[X2]减小，自然会让方差降下来；
• 基于上述思路，如果让观察 E [ X 2 ] \mathbb E[X^2] E[X2]减小 → X \to X →X减小。 X X X是REINFORCE算法中蒙特卡洛方法采样的样本： X → ∇ log ⁡ π ( A t ∣ S t ; θ ) G t X \to \nabla \log \pi(A_t \mid S_t;\theta)G_t X→∇logπ(At​∣St​;θ)Gt​
• 最直接的做法就是将 G t G_t Gt​减小一个数值(基线)，从而降低采样时产生的梯度方差：

基线REINFORCE推导过程

上述的基线数值不能随意去减，减下去的数值需要满足一个条件： 基线数值的去除 理论上不影响策略梯度 ∇ J ( θ ) \nabla \mathcal J(\theta) ∇J(θ)的变化；

进行如下假设： 假设基线数值是关于状态的函数 b ( s ) b(s) b(s)：

• 根据策略梯度定理： 这里并没有使用 E S t ∼ ρ π θ ; A t ∼ π θ [ ∇ log ⁡ π ( A t ∣ S t ; θ ) G t ] \mathbb E_{S_t \sim \rho^{\pi_{\theta}};A_t \sim \pi_{\theta}}[\nabla \log \pi(A_t \mid S_t;\theta)G_t] ESt​∼ρπθ​;At​∼πθ​​[∇logπ(At​∣St​;θ)Gt​]进行推导，因为log函数没有办法处理掉。 ∇ J ( θ ) ∝ ∑ s ∈ S μ ( s ) ∑ a ∈ A q π ( s , a ) ∇ π ( a ∣ s ; θ ) \nabla \mathcal J(\theta) \propto \sum_{s \in \mathcal S}\mu(s) \sum_{a \in \mathcal A}q_\pi(s,a) \nabla \pi(a \mid s;\theta) ∇J(θ)∝s∈S∑​μ(s)a∈A∑​qπ​(s,a)∇π(a∣s;θ)

• 我们将 q π ( s , a ) q_\pi(s,a) qπ​(s,a)( G t G_t Gt​的期望)减去一个 b ( s ) b(s) b(s)： ∑ s ∈ S μ ( s ) ∑ a ∈ A ( q π ( s , a ) − b ( s ) ) ∇ π ( a ∣ s ; θ ) \sum_{s \in \mathcal S}\mu(s) \sum_{a \in \mathcal A}(q_\pi(s,a) - b(s)) \nabla \pi(a \mid s;\theta) s∈S∑​μ(s)a∈A∑​(qπ​(s,a)−b(s))∇π(a∣s;θ) 减掉的baseline部分表示如下： ∑ s ∈ S μ ( s ) ∑ a ∈ A b ( s ) ∇ π ( a ∣ s ; θ ) \sum_{s \in \mathcal S}\mu(s) \sum_{a \in \mathcal A} b(s) \nabla \pi(a \mid s;\theta) s∈S∑​μ(s)a∈A∑​b(s)∇π(a∣s;θ)

• 对上式进行整理，由于 b ( s ) b(s) b(s)中不含动作 a a a，因此在 ∑ a ∈ A \sum_{a \in \mathcal A} ∑a∈A​运算中视作常数，并将梯度符号 ∇ \nabla ∇移到前面： ∑ s ∈ S μ ( s ) × b ( s ) ∇ ∑ a ∈ A π ( a ∣ s ; θ ) \sum_{s \in \mathcal S}\mu(s) \times b(s) \nabla \sum_{a \in \mathcal A} \pi(a \mid s;\theta) s∈S∑​μ(s)×b(s)∇a∈A∑​π(a∣s;θ) 由于策略函数 π ( a ∣ s ; θ ) \pi(a \mid s;\theta) π(a∣s;θ)本质依然是关于 a a a的概率分布，因此， ∑ a ∈ A π ( a ∣ s ; θ ) \sum_{a \in \mathcal A} \pi(a \mid s;\theta) ∑a∈A​π(a∣s;θ)本质上是求动作 a a a的边缘概率。因此则有： 相反，如果一开始选择的函数是关于‘状态、动作两个变量的函数’b(s,a)，该步骤则无法使用‘边缘概率’进行化简。 ∑ a ∈ A π ( a ∣ s ; θ ) = 1 \sum_{a \in \mathcal A} \pi(a \mid s;\theta) = 1 a∈A∑​π(a∣s;θ)=1

• 对结果进行整理，又因为常数的梯度为0，因此，被去除的基线数值的梯度结果为0： ∑ s ∈ S μ ( s ) × b ( s ) ∇ ∑ a ∈ A π ( a ∣ s ; θ ) = ∑ s ∈ S μ ( s ) × b ( s ) ∇ 1 = ∑ s ∈ S μ ( s ) × b ( s ) × 0 = 0 \begin{split} & \sum_{s \in \mathcal S}\mu(s) \times b(s) \nabla \sum_{a \in \mathcal A} \pi(a \mid s;\theta) \\ & = \sum_{s \in \mathcal S}\mu(s) \times b(s) \nabla 1\\ & = \sum_{s \in \mathcal S}\mu(s) \times b(s) \times 0 \\ & = 0 \end{split} ​s∈S∑​μ(s)×b(s)∇a∈A∑​π(a∣s;θ)=s∈S∑​μ(s)×b(s)∇1=s∈S∑​μ(s)×b(s)×0=0​

• 因此，基线数值的去除 理论上不影响策略梯度 ∇ J ( θ ) \nabla \mathcal J(\theta) ∇J(θ)的变化： ∑ s ∈ S μ ( s ) ∑ a ∈ A ( q π ( s , a ) − b ( s ) ) ∇ π ( a ∣ s ; θ ) = ∑ s ∈ S μ ( s ) ∑ a ∈ A q π ( s , a ) ∇ π ( a ∣ s ; θ ) − ∑ s ∈ S μ ( s ) ∑ a ∈ A b ( s ) ∇ π ( a ∣ s ; θ ) = ∑ s ∈ S μ ( s ) ∑ a ∈ A q π ( s , a ) ∇ π ( a ∣ s ; θ ) − 0 = ∑ s ∈ S μ ( s ) ∑ a ∈ A q π ( s , a ) ∇ π ( a ∣ s ; θ ) = ∇ J ( θ ) \begin{split} & \sum_{s \in \mathcal S}\mu(s) \sum_{a \in \mathcal A}(q_\pi(s,a) - b(s)) \nabla \pi(a \mid s;\theta) \\ & = \sum_{s \in \mathcal S}\mu(s) \sum_{a \in \mathcal A}q_\pi(s,a) \nabla \pi(a \mid s;\theta) - \sum_{s \in \mathcal S}\mu(s) \sum_{a \in \mathcal A} b(s) \nabla \pi(a \mid s;\theta) \\ & = \sum_{s \in \mathcal S}\mu(s) \sum_{a \in \mathcal A}q_\pi(s,a) \nabla \pi(a \mid s;\theta) - 0 \\ & = \sum_{s \in \mathcal S}\mu(s) \sum_{a \in \mathcal A}q_\pi(s,a) \nabla \pi(a \mid s;\theta) = \nabla \mathcal J(\theta) \end{split} ​s∈S∑​μ(s)a∈A∑​(qπ​(s,a)−b(s))∇π(a∣s;θ)=s∈S∑​μ(s)a∈A∑​qπ​(s,a)∇π(a∣s;θ)−s∈S∑​μ(s)a∈A∑​b(s)∇π(a∣s;θ)=s∈S∑​μ(s)a∈A∑​qπ​(s,a)∇π(a∣s;θ)−0=s∈S∑​μ(s)a∈A∑​qπ​(s,a)∇π(a∣s;θ)=∇J(θ)​

最终，基线REINFORCE的策略梯度计算公式如下： ∇ J ( θ ) = E S t ∼ ρ π θ ; A t ∼ π θ [ ∇ log ⁡ π ( A t ∣ S t ; θ ) ( G t − b ( S t ) ) ] \nabla \mathcal J(\theta) = \mathbb E_{S_t \sim \rho^{\pi_{\theta}};A_t \sim \pi_{\theta}}[\nabla \log \pi(A_t \mid S_t;\theta)(G_t - b(S_t))] ∇J(θ)=ESt​∼ρπθ​;At​∼πθ​​[∇logπ(At​∣St​;θ)(Gt​−b(St​))] 参数 θ \theta θ的更新方程公式如下： θ t + 1 = θ t + α ∇ log ⁡ π ( A t ∣ S t ; θ t ) ( G t − b ( S t ) ) \theta_{t+1} = \theta_{t} + \alpha \nabla \log \pi (A_t \mid S_t;\theta_{t})(G_t - b(S_t)) θt+1​=θt​+α∇logπ(At​∣St​;θt​)(Gt​−b(St​))

基线 b ( S t ) b(S_t) b(St​)的设置

关于状态 S t S_t St​的基线函数并不是一个一成不变的常数，为了更好地利用基线函数，我们使用一个参数 w w w来学习基线函数的结果，记作 b ^ ( S t , w ) \hat b(S_t,w) b^(St​,w)。 θ t + 1 = θ t + α ∇ log ⁡ π ( A t ∣ S t ; θ t ) ( G t − b ^ ( S t , w ) ) \theta_{t+1} = \theta_{t} + \alpha \nabla \log \pi (A_t \mid S_t;\theta_{t})(G_t - \hat b(S_t,w)) θt+1​=θt​+α∇logπ(At​∣St​;θt​)(Gt​−b^(St​,w)) 如何评判新的基线函数？(如何优化参数 w w w,使得 b ^ ( S t , w ) \hat b(S_t,w) b^(St​,w)最优)

• 对于状态-动作价值较大的状态 → \to → 设置一个较大的基线对动作进行区分；
• 对于状态-动作价值较小的状态 → \to → 设置一个较小的基线对动作进行区分；

从算法的角度观察上述两个条件： 无论状态-动作价值多大 → \to → 都希望基线函数结果 b ^ ( S t , w ) \hat b(S_t,w) b^(St​,w)越靠近 G t G_t Gt​越好。即： 这种思路可以理解为 -> 基线函数中的参数 w 与‘状态动作价值’之间相匹配； G t − b ^ ( S t , w ) → 0 G_t - \hat b(S_t,w) \to 0 Gt​−b^(St​,w)→0 并且还要使用该结果对参数 θ \theta θ进行更新， G t − b ^ ( S t , w ) G_t - \hat b(S_t,w) Gt​−b^(St​,w)越小， θ \theta θ就更新越慢，最终实现收敛。

带基线的REINFORCE代码实现

以CartPole-v1任务为例，首先设置常规REINFORCE：

import gym
import numpy as np
import os
from tqdm import trange

import torch
from torch import nn as nn
import torch.nn.functional as F
import torch.optim as optim

from torch.distributions import Categorical
import matplotlib.pyplot as plt

os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"

env = gym.make("CartPole-v1")
env.seed(543)
torch.manual_seed(543)

env_dict = {
    "env_states":env.observation_space.shape[0],
    "env_actions":env.action_space.n,
    "gamma":0.99,
}


class NormalPolicy(nn.Module):
    def __init__(self,n_state,n_output):
        super(NormalPolicy, self).__init__()

        self.linear_1 = nn.Linear(n_state,128)
        self.dropout = nn.Dropout(p=0.6)
        self.linear_2 = nn.Linear(128,n_output)

        self.saved_log_probs = []
        self.rewards = []

    def forward(self,x):
        x = self.linear_1(x)
        x = self.dropout(x)
        x = F.relu(x)
        action_scores = self.linear_2(x)
        # 将动作离散分布 -> 指数族分布;
        return F.softmax(action_scores,dim=1)


def get_adam_optimizer(policy,lr):
    optimizer = optim.Adam(policy.parameters(),lr)
    return optimizer


Policy = NormalPolicy(env_dict["env_states"],env_dict["env_actions"])
optimizer_normal = get_adam_optimizer(Policy,0.01)


def select_action(state,policy):
    state = torch.from_numpy(state).unsqueeze(0).float()
    probs = policy(state)
    m = Categorical(probs)
    action = m.sample()
    # 存储logπ,在反向传播过程中与Gt相乘，作为损失函数;
    policy.saved_log_probs.append(m.log_prob(action))
    return action.item()

def finish_episode_of_normal(optimizer):
    R = 0
    eps = np.finfo(np.float32).eps.item()
    policy_loss = []
    rewards = []
    for r in Policy.rewards[::-1]:
        R = r + env_dict["gamma"] * R
        rewards.insert(0, R)
    rewards = torch.tensor(rewards)
    # rewards 做了标准化;
    rewards = (rewards - rewards.mean()) / (rewards.std() + eps)
    for log_prob, reward in zip(Policy.saved_log_probs, rewards):
        policy_loss.append(-1 * log_prob * reward)
    optimizer.zero_grad()
    policy_loss = torch.cat(policy_loss).sum()
    policy_loss.backward()
    optimizer.step()
    del Policy.rewards[:]
    del Policy.saved_log_probs[:]


def reinforce_normal(env):
    running_reward = 10
    i_episodes = []
    running_rewards = []

    for i_episode in trange(1000):
        state = env.reset()
        ep_reward = 0

        for t in range(1000):
            action = select_action(state,Policy)
            state,reward,done,_ = env.step(action)
            Policy.rewards.append(reward)
            ep_reward += reward
            if done:
                break

        running_reward = 0.05 * ep_reward + (1 - 0.05) * running_reward
        finish_episode_of_normal(optimizer_normal)
        running_rewards.append(running_reward)
        i_episodes.append(i_episode)

    return i_episodes,running_rewards

if __name__ == '__main__':
    i_episodes,running_rewards = reinforce_normal(env)
    plt.plot(i_episodes,running_rewards)
    plt.show()

带基线的REINFORCE：

import torch.nn as nn
import torch.nn.functional as F
import gym
import torch
from torch.distributions import Categorical
import torch.optim as optim
from copy import deepcopy

import matplotlib.pyplot as plt
from torch.nn.utils import clip_grad_norm_
import os
from tqdm import trange
os.environ["KMP_DUPLICATE_LIB_OK"]="True"

render = False
class Policy(nn.Module):
    def __init__(self,n_states, n_hidden, n_output):
        super(Policy, self).__init__()
        self.linear1 = nn.Linear(n_states, n_hidden)
        self.linear2 = nn.Linear(n_hidden, n_output)

        self.reward = []
        self.log_act_probs = []
        self.Gt = []
        self.sigma = []

    def forward(self, x):
        x = F.relu(self.linear1(x).detach())
        output = F.softmax(self.linear2(x), dim= 1)
        # self.act_probs.append(action_probs)
        return output
    
env = gym.make('CartPole-v1')
n_states = env.observation_space.shape[0]
n_actions = env.action_space.n
policy = Policy(n_states, 128, n_actions)
s_value_func = Policy(n_states, 128, 1)
alpha_theta = 1e-3
optimizer_theta = optim.Adam(policy.parameters(), lr=alpha_theta)
gamma = 0.99
seed = 1
env.seed(seed)
torch.manual_seed(seed)

if __name__ == '__main__':
    running_reward = 10
    live_time = []
    i_episodes = []
    for i_episode in trange(1000):
        state, ep_reward = env.reset(), 0
        if render: env.render()
        policy_loss = []
        s_value = []
        state_sequence = []
        log_act_prob = []
        for t in range(1000):
            state = torch.from_numpy(state).unsqueeze(0).float()
            state_sequence.append(deepcopy(state))
            action_probs = policy(state)
            m = Categorical(action_probs)
            action = m.sample()
            m_log_prob = m.log_prob(action)
            log_act_prob.append(m_log_prob)
            action = action.item()
            next_state, re, done, _ = env.step(action)
            if render: env.render()
            policy.reward.append(re)
            ep_reward += re
            if done:
                break
            state = next_state
        running_reward = 0.05 * ep_reward + (1 - 0.05) * running_reward
        i_episodes.append(i_episode)

        live_time.append(running_reward)
        R = 0
        Gt = []

        # get Gt value
        # 开头的项从T-1,T-2,...
        for r in policy.reward[::-1]:
            R = r + gamma * R
            Gt.insert(0, R)

        for i in range(len(Gt)):
            G = Gt[i]
            V = s_value_func(state_sequence[i])
            delta = G - V
            alpha_w = 1e-3
			
			# 通过更新参数w优化b(s,w)
            optimizer_w = optim.Adam(s_value_func.parameters(), lr=alpha_w)
            optimizer_w.zero_grad()
            policy_loss_w = -delta
            policy_loss_w.backward(retain_graph=True)
            clip_grad_norm_(policy_loss_w, 0.1)
            optimizer_w.step()

            # update policy network
            optimizer_theta.zero_grad()
            policy_loss_theta = - log_act_prob[i] * delta
            policy_loss_theta.backward()
            clip_grad_norm_(policy_loss_theta, 0.1)
            optimizer_theta.step()
        del policy.log_act_probs[:]
        del policy.reward[:]

    plt.plot(i_episodes,live_time)
    plt.show()

将两者图像进行对比，对比结果如下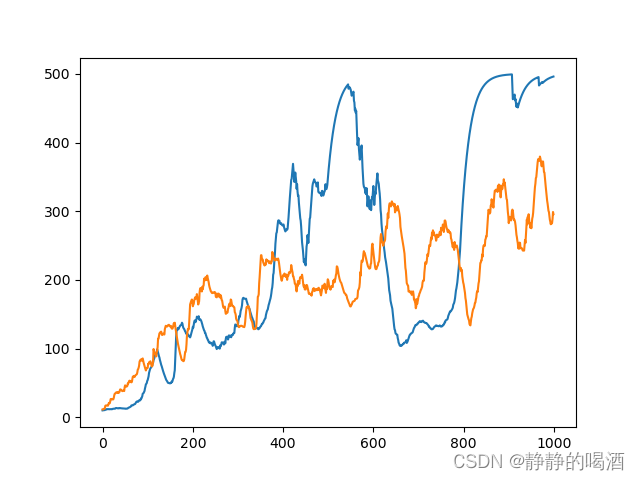： 其中横坐标表示情节个数；纵坐标表示累积的reward结果；

• 蓝色线 表示带基线的REINFORCE；
• 橙色线 表示常规REINFORCE；

可以看出，在更少的情节数量内，带基线的REINFORCE能够更快地得到好的结果并收敛。无论是哪种REINFORCE方法，它的波动都比较高。主要是因为CartPole-v1任务环境本身比较复杂。为了解决该问题，下一节将介绍行动者-评论家框架算法。

相关参考： 【强化学习】策略梯度方法-REINFORCE with Baseline & Actor-Critic 深度强化学习原理、算法pytorch实战 —— 刘全，黄志刚编著