机器学习笔记之EM算法(一)隐变量与EM算法公式的收敛性

引言

从本节开始将介绍EM算法。本节将介绍隐变量以及EM算法公式的收敛性。

隐变量

什么是隐变量？从字面意义来看，就是看不见的变量。或者可以理解为 隐藏在数据内部，表示其隐含规律的变量。通过两个例子，对隐变量进行说明。

示例1

我们面前有若干个非透明的盒子，每个盒子中装有若干个涂有颜色的球，并且 任意一个球均只有一个颜色。此时，有两个人：

• 第一个人是实验员，负责执行实验；
• 另一个人是记录员，负责记录实验过程；

实验目的：推测每个非透明盒子中各颜色球数量的比例，如果 N N N个盒子，自然会得到 N N N个比例结果；

实验员将重复执行如下操作：

• 任意选择一个盒子，并将盒子中的球摇匀；
• 从选择的盒子中抽取一个球；
• 抽取结束后，将球原路放回；

记录员的动作只有一个：记录实验员的整个操作流程。 实际上，实验员每次执行重复操作时，记录员都将记录两个信息：

• 实验员选择的盒子编号 k ( k ∈ { 1 , 2 , ⋯   , N } ) k \quad (k \in \{1,2,\cdots,N\}) k(k∈{1,2,⋯,N})；
• 实验员在编号 k k k盒子中选取的球的颜色。

随着实验员重复执行的次数越多，记录员记录结果越多，我们可以通过记录得到每个袋子球的颜色比例： P i ( k ) ≈ N i ( k ) N ( k ) P_i^{(k)} \approx \frac{N_i^{(k)}}{N^{(k)}} Pi(k)​≈N(k)Ni(k)​​ 其中 P i ( k ) P_i^{(k)} Pi(k)​表示编号为 k k k的盒子中颜色为 i i i的球数量的比例； N ( k ) N^{(k)} N(k)表示整个记录结果中，实验员选择编号 k k k盒子的次数； N i ( k ) N_i^{(k)} Ni(k)​表示 实验员选择编号 k k k盒子条件下，抽取颜色为 i i i的球的数量。 基于中心极限定理，记录的结果越多，推测的结果就越准确。

如果在记录员和实验员之间加一个帘子，使得记录员无法观察实验员时从哪个盒子中抽取的球，只能观察实验员每次操作中抽取球的颜色。 至此，由于选择盒子的过程无法观测到，导致即便再多的记录，也很难直观推测各盒子中各颜色求数量比例。此时，选择盒子的信息就相当于一个隐变量。

示例2

已知 X = { x ( 1 ) , x ( 2 ) , ⋯   , x ( N ) } \mathcal X = \{x^{(1)},x^{(2)},\cdots,x^{(N)}\} X={x(1),x(2),⋯,x(N)}是由概率模型 P ( X ∣ θ ) P(\mathcal X\mid \theta) P(X∣θ)产生的一组样本集合。并且任意一个样本点 x ( i ) ( i = 1 , 2 , ⋯   , N ) x^{(i)}(i=1,2,\cdots,N) x(i)(i=1,2,⋯,N)是一个2维向量。即： x ( i ) = ( x 1 ( i ) , x 2 ( i ) ) ( i = 1 , 2 , … , N ) x^{(i)} = (x_1^{(i)},x_2^{(i)})\quad(i=1,2,\dots,N) x(i)=(x1(i)​,x2(i)​)(i=1,2,…,N) 该样本集合在2维样本空间中的分布如下所示：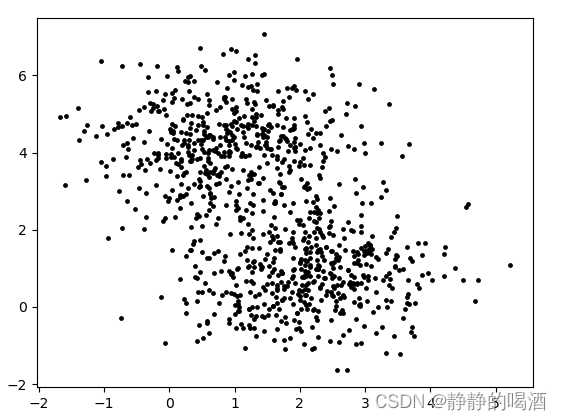

• 从对上图观测的角度我们可能会发现：上面的样本像是分成了两堆。
• 但是这个结果仅凭单纯的观察样本集合，我们是很难观测出来的，样本分成两堆这个信息是通过将样本映射到样本空间中得到的隐藏在样本集合中的信息。

如果我们将上述图像 染个色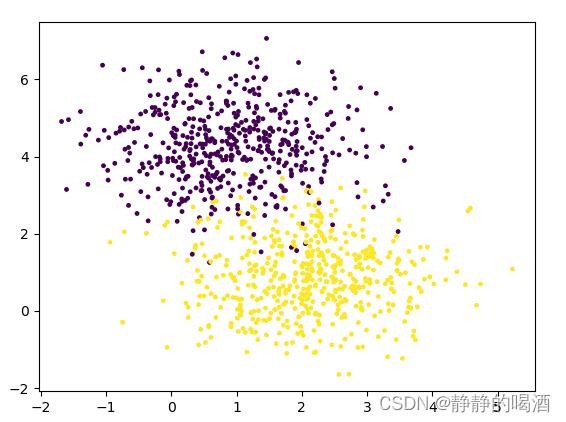： 我们可以直观发现：概率模型 P ( X ∣ θ ) P(\mathcal X \mid \theta) P(X∣θ)描述的是两个不同分布放在一起的效果。基于染色信息，可以对各颜色样本点的分布进行推测，从而推测整个概率模型。 我们也可以称这个染色信息(分类信息)为隐变量。

综合上述两个例子，隐变量存在的特性：

隐变量是样本集合中一种 无法直接观测的规律，但是对概率模型的状态、对输出结果存在影响的一种信息。

EM算法 包含隐变量的混合概率模型

基于上述对隐变量的介绍，我们可以将概率模型分为两类：

• 简单模型：对于一个概率模型 P ( X ∣ θ ) P(\mathcal X \mid \theta) P(X∣θ)，它的模型参数 θ \theta θ可以 仅通过 P ( X ∣ θ ) P(\mathcal X \mid \theta) P(X∣θ)生成的样本集合 X \mathcal X X进行求解。 关于 θ \theta θ解析解的求解方式是极大似然估计(Maximum Likelihood Estimate，MLE)： 为了简化运算，通常添加一个log,对log likelihood求解最大值: θ ^ = arg ⁡ max ⁡ θ log ⁡ P ( X ∣ θ ) \hat {\theta} = \mathop{\arg\max}\limits_{\theta} \log P(\mathcal X \mid \theta) θ^=θargmax​logP(X∣θ)
• 复杂模型：基于上述两个示例，存在一些信息 仅通过直接观测样本集合 X \mathcal X X直接求解模型参数 θ \theta θ是非常困难的。 因而，将无法直接观测到的隐含信息具象化为一个变量：隐变量。用 Z \mathcal Z Z表示。此时，概率模型将成为一个关于 X \mathcal X X和 Z \mathcal Z Z的混合模型： P ( X , Z ∣ θ ) P(\mathcal X,\mathcal Z \mid \theta) P(X,Z∣θ) 通常称： X \mathcal X X为观测变量：通过样本集合直接观测到的信息； Z \mathcal Z Z称为隐变量：样本集合中无法直接观测到的隐藏信息。 将 X \mathcal X X和 Z \mathcal Z Z合并在一起，称为 完整数据。

EM算法的表达形式

EM算法就是针对包含隐变量的混合概率模型 P ( X , Z ∣ θ ) P(\mathcal X,\mathcal Z \mid \theta) P(X,Z∣θ)求解最优模型参数 θ \theta θ的一种方法。其算法公式表示如下： θ ( t + 1 ) = arg ⁡ max ⁡ θ { ∫ Z log ⁡ P ( X , Z ∣ θ ) ⋅ P ( Z ∣ X , θ ( t ) ) d Z } \theta^{(t+1)} = \mathop{\arg\max}\limits_{\theta} \left\{\int_{\mathcal Z} \log P(\mathcal X,\mathcal Z \mid \theta)\cdot P(\mathcal Z \mid \mathcal X,\theta^{(t)})d\mathcal Z\right\} θ(t+1)=θargmax​{∫Z​logP(X,Z∣θ)⋅P(Z∣X,θ(t))dZ} 观察该公式：

• 首先，它并没有直接求解出模型参数 θ \theta θ的最优解，而是一个关于 θ ( t + 1 ) \theta^{(t+1)} θ(t+1)与 θ ( t ) \theta^{(t)} θ(t)之间的迭代过程；
• P ( Z ∣ X , θ ( t ) ) P(\mathcal Z \mid \mathcal X,\theta^{(t)}) P(Z∣X,θ(t))表示：给定 t t t时刻(或者说上一时刻)的模型参数 θ ( t ) \theta^{(t)} θ(t)和观测变量 X \mathcal X X条件下，隐变量 Z \mathcal Z Z的后验概率；
• log ⁡ P ( X , Z ∣ θ ) \log P(\mathcal X,\mathcal Z \mid \theta) logP(X,Z∣θ)是基于 完整数据 X , Z \mathcal X,\mathcal Z X,Z的 log ⁡ \log log似然结果。

因此，可以将上述公式括号中的部分看作：基于后验概率 P ( Z ∣ X , θ ( t ) ) P(\mathcal Z \mid \mathcal X,\theta^{(t)}) P(Z∣X,θ(t))分布的关于 log ⁡ P ( X , Z ∣ θ ) \log P(\mathcal X,\mathcal Z \mid \theta) logP(X,Z∣θ)的期望结果： ∫ Z log ⁡ P ( X , Z ∣ θ ) ⋅ P ( Z ∣ X , θ ( t ) ) d Z = E Z ∣ X , θ ( t ) [ log ⁡ P ( X , Z ∣ θ ) ] \int_{\mathcal Z} \log P(\mathcal X,\mathcal Z \mid \theta)\cdot P(\mathcal Z \mid \mathcal X,\theta^{(t)})d\mathcal Z = \mathbb E_{\mathcal Z \mid \mathcal X,\theta^{(t)}} \left[\log P(\mathcal X,\mathcal Z \mid \theta)\right] ∫Z​logP(X,Z∣θ)⋅P(Z∣X,θ(t))dZ=EZ∣X,θ(t)​[logP(X,Z∣θ)] 并称上述求解期望的过程为EM算法中的E部(Expectation-step)； 将当前时刻最优模型参数 θ ( t + 1 ) \theta^{(t+1)} θ(t+1)的求解过程称为M部； θ ( t + 1 ) = arg ⁡ max ⁡ θ { E Z ∣ X , θ ( t ) [ log ⁡ P ( X , Z ∣ θ ) ] } \theta^{(t+1)} = \mathop{\arg\max}\limits_{\theta} \left\{\mathbb E_{\mathcal Z \mid \mathcal X,\theta^{(t)}} \left[\log P(\mathcal X,\mathcal Z \mid \theta)\right]\right\} θ(t+1)=θargmax​{EZ∣X,θ(t)​[logP(X,Z∣θ)]}

EM算法的收敛性

EM算法的标准计算框架是由E步和M步交替组成，而算法的收敛性可以确保每次迭代得到的模型参数 θ ( t + 1 ) \theta^{(t+1)} θ(t+1)优于之前迭代得到的模型参数 θ ( t ) , θ ( t − 1 ) , ⋯ \theta^{(t)},\theta^{(t-1)},\cdots θ(t),θ(t−1),⋯，从而最终至少逼近局部最优值。下面将证明EM算法的收敛性。

EM算法的收敛性证明的条件与目标

描述EM算法收敛性的核心是：通过EM算法迭代得到的 θ ( t + 1 ) \theta^{(t+1)} θ(t+1)对于概率模型的表示： P ( X ∣ θ ( t + 1 ) ) P(\mathcal X \mid \theta^{(t+1)}) P(X∣θ(t+1))优于 θ ( t ) \theta^{(t)} θ(t)对于概率模型的表示： P ( X ∣ θ ( t ) ) P(\mathcal X \mid \theta^{(t)}) P(X∣θ(t))。从极大似然估计的角度表示： 注意：这里使用的是’概率模型‘ P ( X ∣ θ ) P(\mathcal X \mid \theta) P(X∣θ)而不是'概率混合模型' P ( X , Z ∣ θ ) P(\mathcal X,\mathcal Z \mid \theta) P(X,Z∣θ),因为’隐变量‘这个概念是人为定义的，在真实情况中，数据集合内只有观测变量 X \mathcal X X； log ⁡ P ( X ∣ θ ( t ) ) ≤ log ⁡ P ( X ∣ θ ( t + 1 ) ) \log P(\mathcal X \mid \theta^{(t)}) \leq \log P(\mathcal X \mid \theta^{(t+1)}) logP(X∣θ(t))≤logP(X∣θ(t+1)) 综上，我们确定了 算法收敛性证明的条件：EM算法自身。 θ ( t + 1 ) = arg ⁡ max ⁡ θ { ∫ Z log ⁡ P ( X , Z ∣ θ ) ⋅ P ( Z ∣ X , θ ( t ) ) d Z } \theta^{(t+1)} = \mathop{\arg\max}\limits_{\theta} \left\{\int_{\mathcal Z} \log P(\mathcal X,\mathcal Z \mid \theta)\cdot P(\mathcal Z \mid \mathcal X,\theta^{(t)})d\mathcal Z\right\} θ(t+1)=θargmax​{∫Z​logP(X,Z∣θ)⋅P(Z∣X,θ(t))dZ} 并确定了描述算法收敛性证明的目标： log ⁡ P ( X ∣ θ ( t ) ) ≤ log ⁡ P ( X ∣ θ ( t + 1 ) ) \log P(\mathcal X \mid \theta^{(t)}) \leq \log P(\mathcal X \mid \theta^{(t+1)}) logP(X∣θ(t))≤logP(X∣θ(t+1))

EM算法的收敛性证明过程

具体证明如下：

• 将隐变量 Z \mathcal Z Z引入 log ⁡ P ( X ∣ θ ) \log P(\mathcal X \mid \theta) logP(X∣θ)中： 联合概率与条件概率~ log ⁡ P ( X ∣ θ ) = log ⁡ P ( X , Z ∣ θ ) P ( Z ∣ X , θ ) = log ⁡ P ( X , Z ∣ θ ) − log ⁡ P ( Z ∣ X , θ ) \log P(\mathcal X \mid \theta) = \log \frac{P(\mathcal X,\mathcal Z \mid \theta)}{P(\mathcal Z \mid \mathcal X,\theta)} = \log P(\mathcal X,\mathcal Z \mid \theta) - \log P(\mathcal Z \mid \mathcal X,\theta) logP(X∣θ)=logP(Z∣X,θ)P(X,Z∣θ)​=logP(X,Z∣θ)−logP(Z∣X,θ)
• 针对上述公式等式两端求积分。对分布 P ( Z ∣ X , θ ( t ) ) P(\mathcal Z \mid \mathcal X,\theta^{(t)}) P(Z∣X,θ(t))求解积分：

  • 对 log ⁡ P ( X ∣ θ ) \log P(\mathcal X \mid \theta) logP(X∣θ)求解积分： ∫ Z P ( Z ∣ X , θ ( t ) ) ⋅ log ⁡ P ( X ∣ θ ) d Z \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \cdot \log P(\mathcal X \mid \theta) d\mathcal Z ∫Z​P(Z∣X,θ(t))⋅logP(X∣θ)dZ 由于 log ⁡ P ( X ∣ θ ) \log P(\mathcal X \mid \theta) logP(X∣θ)中不含 Z \mathcal Z Z项，因此在求积分过程中将其视为常数，并将其提到积分号外面： log ⁡ P ( X ∣ θ ) ∫ Z P ( Z ∣ X , θ ( t ) ) d Z \log P(\mathcal X \mid \theta)\int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)})d\mathcal Z logP(X∣θ)∫Z​P(Z∣X,θ(t))dZ 根据条件概率密度积分的定义(动态规划强化学习任务中介绍过)，有： ∫ Z P ( Z ∣ X , θ ( t ) ) d Z = 1 \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)})d\mathcal Z = 1 ∫Z​P(Z∣X,θ(t))dZ=1 最终对 log ⁡ P ( X ∣ θ ) \log P(\mathcal X \mid \theta) logP(X∣θ)求解积分结果没有变化，依然是 log ⁡ P ( X ∣ θ ) \log P(\mathcal X \mid \theta) logP(X∣θ)自身： log ⁡ P ( X ∣ θ ) ∫ Z P ( Z ∣ X , θ ( t ) ) d Z = log ⁡ P ( X ∣ θ ) ⋅ 1 = log ⁡ P ( X ∣ θ ) \log P(\mathcal X \mid \theta)\int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)})d\mathcal Z = \log P(\mathcal X \mid \theta) \cdot 1 = \log P(\mathcal X \mid \theta) logP(X∣θ)∫Z​P(Z∣X,θ(t))dZ=logP(X∣θ)⋅1=logP(X∣θ)

  • log ⁡ P ( X , Z ∣ θ ) − log ⁡ P ( Z ∣ X , θ ) \log P(\mathcal X,\mathcal Z \mid \theta) - \log P(\mathcal Z \mid \mathcal X,\theta) logP(X,Z∣θ)−logP(Z∣X,θ)对分布 P ( Z ∣ X , θ ( t ) ) P(\mathcal Z \mid \mathcal X,\theta^{(t)}) P(Z∣X,θ(t))求解积分： ∫ Z P ( Z ∣ X , θ ( t ) ) [ log ⁡ P ( X , Z ∣ θ ) − log ⁡ P ( Z ∣ X , θ ) ] d Z \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \left[\log P(\mathcal X,\mathcal Z \mid \theta) - \log P(\mathcal Z \mid \mathcal X,\theta)\right]d\mathcal Z ∫Z​P(Z∣X,θ(t))[logP(X,Z∣θ)−logP(Z∣X,θ)]dZ 将上式展开： ∫ Z P ( Z ∣ X , θ ( t ) ) log ⁡ P ( X , Z ∣ θ ) d Z − ∫ Z P ( Z ∣ X , θ ( t ) ) log ⁡ P ( Z ∣ X , θ ) d Z \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)})\log P(\mathcal X,\mathcal Z \mid \theta) d\mathcal Z - \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \log P(\mathcal Z \mid \mathcal X,\theta)d\mathcal Z ∫Z​P(Z∣X,θ(t))logP(X,Z∣θ)dZ−∫Z​P(Z∣X,θ(t))logP(Z∣X,θ)dZ 观察上述结果是两项相减的形式。对上述两项进行如下定义： 将上述两项均定义为关于 θ , θ ( t ) \theta,\theta^{(t)} θ,θ(t)的函数; Q ( θ , θ ( t ) ) = ∫ Z P ( Z ∣ X , θ ( t ) ) log ⁡ P ( X , Z ∣ θ ) d Z H ( θ , θ ( t ) ) = ∫ Z P ( Z ∣ X , θ ( t ) ) log ⁡ P ( Z ∣ X , θ ) d Z \mathcal Q(\theta,\theta^{(t)}) = \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)})\log P(\mathcal X,\mathcal Z \mid \theta) d\mathcal Z \\ \mathcal H(\theta,\theta^{(t)}) = \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \log P(\mathcal Z \mid \mathcal X,\theta)d\mathcal Z Q(θ,θ(t))=∫Z​P(Z∣X,θ(t))logP(X,Z∣θ)dZH(θ,θ(t))=∫Z​P(Z∣X,θ(t))logP(Z∣X,θ)dZ 原式则有： log ⁡ P ( X ∣ θ ) = Q ( θ , θ ( t ) ) − H ( θ , θ ( t ) ) \log P(\mathcal X \mid \theta) = \mathcal Q(\theta,\theta^{(t)}) - \mathcal H(\theta,\theta^{(t)}) logP(X∣θ)=Q(θ,θ(t))−H(θ,θ(t)) 首先观察 Q ( θ , θ ( t ) ) \mathcal Q(\theta,\theta^{(t)}) Q(θ,θ(t))，该式即EM算法的E部。根据EM算法(收敛性证明条件)，有： 根据EM算法定义得到 Q ( θ ( t + 1 ) , θ ( t ) ) ≥ Q ( θ , θ ( t ) ) ∀ θ \mathcal Q(\theta^{(t+1)},\theta^{(t)}) \geq \mathcal Q(\theta,\theta^{(t)}) \quad \forall \theta Q(θ(t+1),θ(t))≥Q(θ,θ(t))∀θ 基于上式，自然有： θ ( t ) ∈ ∀ θ Q ( θ ( t + 1 ) , θ ( t ) ) ≥ Q ( θ ( t ) , θ ( t ) ) → Q ( θ ( t + 1 ) , θ ( t ) ) − Q ( θ ( t ) , θ ( t ) ) ≥ 0 \theta^{(t)} \in \forall \theta \\ \mathcal Q(\theta^{(t+1)},\theta^{(t)}) \geq \mathcal Q(\theta^{(t)},\theta^{(t)}) \to \mathcal Q(\theta^{(t+1)},\theta^{(t)}) - \mathcal Q(\theta^{(t)},\theta^{(t)}) \geq 0 θ(t)∈∀θQ(θ(t+1),θ(t))≥Q(θ(t),θ(t))→Q(θ(t+1),θ(t))−Q(θ(t),θ(t))≥0 继续观察 H ( θ , θ ( t ) ) \mathcal H(\theta,\theta^{(t)}) H(θ,θ(t))，和 Q ( θ , θ ( t ) ) Q(\theta,\theta^{(t)}) Q(θ,θ(t))处理方式类似，观察 H ( θ ( t + 1 ) , θ ( t ) ) \mathcal H(\theta^{(t+1)},\theta^{(t)}) H(θ(t+1),θ(t))和 H ( θ ( t ) , θ ( t ) ) \mathcal H(\theta^{(t)},\theta^{(t)}) H(θ(t),θ(t))之间的大小关系。即： H ( θ ( t + 1 ) , θ ( t ) ) − H ( θ ( t ) , θ ( t ) ) = ? 0 \mathcal H(\theta^{(t+1)},\theta^{(t)}) - \mathcal H(\theta^{(t)},\theta^{(t)}) \overset{\text{?}}{=} 0 H(θ(t+1),θ(t))−H(θ(t),θ(t))=?0 将上述公式展开： ∫ Z P ( Z ∣ X , θ ( t ) ) log ⁡ P ( Z ∣ X , θ ( t + 1 ) ) d Z − ∫ Z P ( Z ∣ X , θ ( t ) ) log ⁡ P ( Z ∣ X , θ ( t ) ) d Z \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \log P(\mathcal Z \mid \mathcal X,\theta^{(t+1)})d\mathcal Z - \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \log P(\mathcal Z \mid \mathcal X,\theta^{(t)})d\mathcal Z ∫Z​P(Z∣X,θ(t))logP(Z∣X,θ(t+1))dZ−∫Z​P(Z∣X,θ(t))logP(Z∣X,θ(t))dZ 提出公因式 P ( Z ∣ X , θ ( t ) ) P(\mathcal Z \mid \mathcal X,\theta^{(t)}) P(Z∣X,θ(t))： ∫ Z P ( Z ∣ X , θ ( t ) ) [ log ⁡ P ( Z ∣ X , θ ( t + 1 ) ) − log ⁡ P ( Z ∣ X , θ ( t ) ) ] d Z = ∫ Z P ( Z ∣ X , θ ( t ) ) [ log ⁡ P ( Z ∣ X , θ ( t + 1 ) ) P ( Z ∣ X , θ ( t ) ) ] d Z \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)})\left[\log P(\mathcal Z \mid \mathcal X,\theta^{(t+1)}) - \log P(\mathcal Z \mid \mathcal X,\theta^{(t)})\right] d\mathcal Z \\ = \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \left[\log \frac{P(\mathcal Z \mid \mathcal X,\theta^{(t+1)})}{P(\mathcal Z \mid \mathcal X,\theta^{(t)})}\right] d\mathcal Z ∫Z​P(Z∣X,θ(t))[logP(Z∣X,θ(t+1))−logP(Z∣X,θ(t))]dZ=∫Z​P(Z∣X,θ(t))[logP(Z∣X,θ(t))P(Z∣X,θ(t+1))​]dZ 该格式是 K L \mathcal K\mathcal L KL散度的格式： KL散度是描述概率分布差距的一种方式，其结果 ≥ 0 \geq0 ≥0恒成立，先挖一个坑把~ ∫ Z P ( Z ∣ X , θ ( t ) ) [ log ⁡ P ( Z ∣ X , θ ( t + 1 ) ) P ( Z ∣ X , θ ( t ) ) ] d Z = − K L ( P ( Z ∣ X , θ ( t ) ) ∣ ∣ P ( Z ∣ X , θ ( t + 1 ) ) ) ≤ 0 \int_{\mathcal Z}P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \left[\log \frac{P(\mathcal Z \mid \mathcal X,\theta^{(t+1)})}{P(\mathcal Z \mid \mathcal X,\theta^{(t)})}\right] d\mathcal Z = - \mathcal K\mathcal L(P(\mathcal Z \mid \mathcal X,\theta^{(t)}) || P(\mathcal Z \mid \mathcal X,\theta^{(t+1)})) \leq 0 ∫Z​P(Z∣X,θ(t))[logP(Z∣X,θ(t))P(Z∣X,θ(t+1))​]dZ=−KL(P(Z∣X,θ(t))∣∣P(Z∣X,θ(t+1)))≤0 因此，则有： H ( θ ( t + 1 ) , θ ( t ) ) − H ( θ ( t ) , θ ( t ) ) ≤ 0 \mathcal H(\theta^{(t+1)},\theta^{(t)}) - \mathcal H(\theta^{(t)},\theta^{(t)}) \leq 0 H(θ(t+1),θ(t))−H(θ(t),θ(t))≤0 结合 Q ( θ ( t + 1 ) , θ ( t ) ) − Q ( θ ( t ) , θ ( t ) ) ≥ 0 \mathcal Q(\theta^{(t+1)},\theta^{(t)}) - \mathcal Q(\theta^{(t)},\theta^{(t)}) \geq 0 Q(θ(t+1),θ(t))−Q(θ(t),θ(t))≥0，从而有： Q ( θ ( t + 1 ) , θ ( t ) ) − H ( θ ( t + 1 ) , θ ( t ) ) ≥ Q ( θ ( t ) , θ ( t ) ) − H ( θ ( t ) , θ ( t ) ) \mathcal Q(\theta^{(t+1)},\theta^{(t)}) - \mathcal H(\theta^{(t+1)},\theta^{(t)}) \geq \mathcal Q(\theta^{(t)},\theta^{(t)}) - \mathcal H(\theta^{(t)},\theta^{(t)}) Q(θ(t+1),θ(t))−H(θ(t+1),θ(t))≥Q(θ(t),θ(t))−H(θ(t),θ(t)) 最终有： log ⁡ P ( X ∣ θ ( t + 1 ) ) ≥ log ⁡ P ( X ∣ θ ( t ) ) \log P(\mathcal X \mid \theta^{(t+1)}) \geq \log P(\mathcal X \mid \theta^{(t)}) logP(X∣θ(t+1))≥logP(X∣θ(t))

证毕。

总结

• 隐变量 Z \mathcal Z Z是人为设定的，朴素目的是为了更简单地求解概率模型 P ( X ∣ θ ) P(\mathcal X \mid \theta) P(X∣θ)；
• EM算法的收敛性表达了通过EM算法迭代得到的模型参数确实能够更好地表示概率模型，但该模型参数只是局部最优。

相关参考： 机器学习中的隐变量和隐变量模型 最大期望算法-百度百科 机器学习-EM算法1(EM算法公式以及算法收敛性证明)