机器学习笔记之EM算法(三)隐变量与EM算法的本质

引言

上一节介绍了EM算法公式的导出过程，本节将重新回顾EM算法，比对各模型的求解方式，并探究引入隐变量与EM算法的本质。

回顾：EM算法 从性质上介绍EM算法

EM算法本质上是一种算法，它的目标是通过求解参数 θ \theta θ，将概率模型 P ( X ∣ θ ) P(\mathcal X \mid \theta) P(X∣θ)表示出来。 和EM算法具有 相似性质 的如：极大似然估计(MLE)，最大后验概率估计(MAP)： θ ^ M L E = arg ⁡ max ⁡ θ log ⁡ P ( X ∣ θ ) θ ^ M A P ∝ arg ⁡ max ⁡ θ log ⁡ P ( X ∣ θ ) P ( θ ) \hat \theta_{MLE} = \mathop{\arg\max}\limits_{\theta} \log P(\mathcal X \mid \theta) \\ \hat \theta_{MAP} \propto \mathop{\arg\max}\limits_{\theta} \log P(\mathcal X \mid \theta)P(\theta) θ^MLE​=θargmax​logP(X∣θ)θ^MAP​∝θargmax​logP(X∣θ)P(θ)

和上述两种方法不同的是，EM算法并没有求解析解，而是迭代解： 与其说是求解，不如说是对求解过程中‘对解进行优化’。相似方法的有‘梯度下降’~ θ ( t + 1 ) = arg ⁡ max ⁡ θ ∫ Z P ( X , Z ∣ θ ) P ( Z ∣ X , θ ( t ) ) d Z \theta^{(t+1)} = \mathop{\arg\max}\limits_{\theta} \int_{\mathcal Z} P(\mathcal X,\mathcal Z \mid \theta)P(\mathcal Z \mid \mathcal X,\theta^{(t)}) d\mathcal Z θ(t+1)=θargmax​∫Z​P(X,Z∣θ)P(Z∣X,θ(t))dZ 通过EM算法的收敛性证明，可以推导出EM算法在迭代过程中可以对模型参数的解 θ \theta θ进行优化，从而达到一个至少是局部最优的解： log ⁡ P ( X ∣ θ ( t + 1 ) ) ≥ log ⁡ P ( X ∣ θ ( t ) ) \log P(\mathcal X \mid \theta^{(t+1)}) \geq \log P(\mathcal X \mid \theta^{(t)}) logP(X∣θ(t+1))≥logP(X∣θ(t))

其他概念回顾

由于EM算法的算法性质，自然和之前介绍的其他概念存在明显区分：

线性回归

例如之前介绍的很多概念如：线性回归，它的模型只是一个线性函数： f ( W , b ) = W T X + b f(\mathcal W,b) = \mathcal W^{T}\mathcal X + b f(W,b)=WTX+b 基于该模型，如何通过求解模型参数 W , b \mathcal W,b W,b来实现回归任务？因此介绍一种求解模型参数 W , b \mathcal W,b W,b的工具：最小二乘估计： L ( W , b ) = ∑ i = 1 N ∣ ∣ W T x ( i ) + b − y ( i ) ∣ ∣ ( x ( i ) , y ( i ) ) ∈ D a t a \mathcal L(\mathcal W,b) = \sum_{i=1}^N||\mathcal W^{T}x^{(i)} + b - y^{(i)}|| \quad (x^{(i)},y^{(i)}) \in Data L(W,b)=i=1∑N​∣∣WTx(i)+b−y(i)∣∣(x(i),y(i))∈Data 我们要强调的是：最小二乘估计 自身是不能求解最优模型参数，他只是提供了一种 手段，而真正求解最优参数 W ^ , b ^ \hat {\mathcal W},\hat b W^,b^是如下式子： W ^ , b ^ = arg ⁡ min ⁡ W , b L ( W , b ) \hat {\mathcal W},\hat b = \mathop{\arg\min}\limits_{\mathcal W,b} \mathcal L(\mathcal W,b) W^,b^=W,bargmin​L(W,b) 因此，最小二乘估计 L ( W , b ) \mathcal L(\mathcal W,b) L(W,b)通常称之为 策略，还有一个更熟悉的名字：损失函数(Loss Function)。 在介绍线性分类中，在介绍每一种方法时，都会提到一个词：朴素思想。而 朴素思想就是构建策略的心路历程。

感知机算法

例如：感知机算法(perceptron) 它的朴素思想：错误驱动。基于该思想构建的策略是： L ( W , b ) = ∑ ( x ( i ) , y ( i ) ) ∈ D − y ( i ) ( W T x ( i ) + b ) \mathcal L(\mathcal W,b) = \sum_{(x^{(i)},y^{(i)}) \in \mathcal D} -y^{(i)}\left(\mathcal W^{T}x^{(i)} + b\right) L(W,b)=(x(i),y(i))∈D∑​−y(i)(WTx(i)+b) 基于该策略的具体算法是： W ^ , b ^ = arg ⁡ min ⁡ W , b L ( W , b ) \hat {\mathcal W},\hat b = \mathop{\arg\min}\limits_{\mathcal W,b} \mathcal L(\mathcal W,b) W^,b^=W,bargmin​L(W,b)

支持向量机

支持向量机不仅仅只满足于当前样本分类正确，并且它希望分类模型鲁棒性更强，预测结果更加泛化。

以硬间隔SVM为例，它的朴素思想是：基于选择的模型，将样本全部分类正确的条件下，使得距离划分直线(超平面)最近的样本点到直线(超平面)之间的距离最大。

因此，基于该思想的策略表达如下： { max ⁡ W , b min ⁡ x ( i ) ∈ X 1 ∣ ∣ W ∣ ∣ ∣ W T x ( i ) + b ∣ s . t . y ( i ) ( W T x ( i ) + b ) > 0 \begin{cases} \mathop{\max}\limits_{\mathcal W,b} \mathop{\min}\limits_{x^{(i)} \in \mathcal X} \frac{1}{||\mathcal W||} \left|\mathcal W^{T}x^{(i)} + b\right| \\ s.t. \quad y^{(i)} \left(\mathcal W^{T}x^{(i)} + b \right) > 0 \end{cases} ⎩ ⎨ ⎧​W,bmax​x(i)∈Xmin​∣∣W∣∣1​∣ ∣​WTx(i)+b∣ ∣​s.t.y(i)(WTx(i)+b)>0​

我们可以看出，在之前介绍的每一种方法，其核心都是策略的构建，而不是模型本身。甚至整个线性分类都共用同一款模型： f ( W , b ) = s i g n ( W T X + b ) f(\mathcal W,b) = sign(\mathcal W^{T}\mathcal X + b) f(W,b)=sign(WTX+b) 其区别只是在 s i g n sign sign函数连续、不连续而已。

需要使用EM算法求解的问题

回顾关于EM算法公式的相关结论： X = { x ( 1 ) , x ( 2 ) , ⋯   , x ( N ) } Z = { z ( 1 ) , z ( 2 ) , ⋯   , z ( n ) } \mathcal X = \{x^{(1)},x^{(2)},\cdots,x^{(N)}\} \\ \mathcal Z = \{z^{(1)},z^{(2)},\cdots,z^{(n)}\} X={x(1),x(2),⋯,x(N)}Z={z(1),z(2),⋯,z(n)} 其中， X \mathcal X X称为观测变量； Z \mathcal Z Z称为隐变量； ( X , Z ) (\mathcal X,\mathcal Z) (X,Z)称为完备数据(Complete Data)； EM算法求解的概率模型如下： P ( X ∣ θ ) P(\mathcal X \mid \theta) P(X∣θ) 其中， θ \theta θ表示模型参数(Model Parameter); EM算法通过E部(Expectation-step)和M部(Maximization step)交替迭代计算优化模型参数：

• E部操作： E Z ∣ X , θ [ log ⁡ P ( X , Z ∣ θ ) ] \mathbb E_{\mathcal Z \mid \mathcal X,\theta} \left[\log P(\mathcal X,\mathcal Z \mid \theta)\right] EZ∣X,θ​[logP(X,Z∣θ)]
• M部操作： θ ( t + 1 ) = arg ⁡ max ⁡ θ { E Z ∣ X , θ [ log ⁡ P ( X , Z ∣ θ ) ] } \theta^{(t+1)} = \mathop{\arg\max}\limits_{\theta} \left\{\mathbb E_{\mathcal Z \mid \mathcal X,\theta} \left[\log P(\mathcal X,\mathcal Z \mid \theta)\right]\right\} θ(t+1)=θargmax​{EZ∣X,θ​[logP(X,Z∣θ)]}

而EM算法主要应用于求解 概率生成模型 的模型参数。

概率生成模型

在介绍隐变量的过程中我们提到过：隐变量 Z \mathcal Z Z只是一个人为设置的变量，它并不真实存在，从始至终真实存在的只有观测变量 X \mathcal X X。使用概率图对概率生成模型进行表示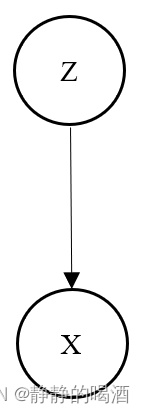： 尽管这个图很抽象，但是概率生成模型实际表达的意思是：以 Z \mathcal Z Z为条件，通过隐变量 Z \mathcal Z Z生成真实的可观测变量 X \mathcal X X。

在介绍线性分类，我们介绍了两个基于软分类的概率生成模型：高斯判别分析(Gaussian Discriminant Analys)和 朴素贝叶斯分类器(Naive BayesClassifier)。

以高斯判别分析为例，高斯判别分析的概率图和上述概率图有一些区别： 可以理解成‘概率生成模型’的一种特殊表示。 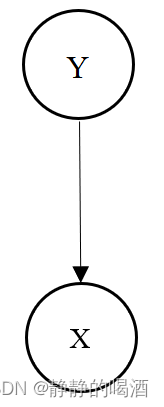区别主要在于高斯判别分析它的隐变量是样本标签赋予的，当然这个样本标签也是人为标注的，但 Y \mathcal Y Y确实也是数据集合的一部分；

但是它的思想和概率生成模型是如出一辙的。

• 基于标签的类别数量，对样本标签的先验分布 P ( Y ) P(\mathcal Y) P(Y)进行假设；(分类分布或者伯努利分布)
• 基于 P ( Y ) P(\mathcal Y) P(Y)确定的条件下，样本针对各标签服从高斯分布。 X ∣ Y ∼ N ( μ , Σ ) \mathcal X \mid \mathcal Y \sim \mathcal N(\mu,\Sigma) X∣Y∼N(μ,Σ)

与高斯判别分析相对应，高斯混合模型(Gaussian Mixture Model,GMM)。从数据集合的角度观察，数据此时不存在标签信息，只剩下样本集合 X \mathcal X X的信息。 因此假设隐变量 Z \mathcal Z Z服从分类分布；

Z \mathcal Z Z12 ⋯ \cdots ⋯ k k k P ( Z ) P(\mathcal Z) P(Z) p 1 p_1 p1​ p 2 p_2 p2​ ⋯ \cdots ⋯ p k p_k pk​

在隐变量 Z \mathcal Z Z分布的条件下，基于样本 X \mathcal X X的条件概率分布 P ( X ∣ Z ) P(\mathcal X\mid \mathcal Z) P(X∣Z)服从高斯分布： P ( X ∣ Z = i ) ∼ N ( μ i , Σ i ) ( i = 1 , 2 , ⋯   , k ) P(\mathcal X \mid \mathcal Z = i) \sim \mathcal N(\mu_i,\Sigma_i) \quad (i=1,2,\cdots,k) P(X∣Z=i)∼N(μi​,Σi​)(i=1,2,⋯,k)

在求解过程中，都是对联合概率分布进行建模。 依然以高斯判别分析为例:

• 它的策略是基于联合概率分布 P ( X , Y ) P(\mathcal X,\mathcal Y) P(X,Y)的 log ⁡ \log log似然函数； 需要假设‘各样本间相互独立’。
• 算法部分使用 极大似然估计： L ( θ ) = log ⁡ P ( X , Y ) = log ⁡ ∏ i = 1 N P ( x ( i ) , y ( i ) ) θ ^ = arg ⁡ max ⁡ θ L ( θ ) \mathcal L(\theta) = \log P(\mathcal X,\mathcal Y) = \log \prod_{i=1}^N P(x^{(i)},y^{(i)}) \\ \hat \theta = \mathop{\arg\max}\limits_{\theta} \mathcal L(\theta) L(θ)=logP(X,Y)=logi=1∏N​P(x(i),y(i))θ^=θargmax​L(θ)

高斯混合模型关于隐变量 Z \mathcal Z Z的假设非常简单，只是离散的一维分布。但实际上 Z \mathcal Z Z的假设有很多种形式和结构。在后续遇到时会再次提起。 接着挖坑~

EM算法的本质

再次回到EM算法本身。无论是狭义EM还是广义EM，它对所求解的概率模型是有条件的：

• 观测数据只有 X \mathcal X X；
• 概率模型是关于参数 θ \theta θ的函数。即 通过求解参数 θ \theta θ的方式，再通过参数 θ \theta θ表示概率模型：

但是在之前的介绍中，这种求解模式都是使用极大似然估计去做的： θ ^ = arg ⁡ max ⁡ θ log ⁡ P ( X ∣ θ ) \hat {\theta} = \mathop{\arg\max}\limits_{\theta} \log P(\mathcal X\mid \theta) θ^=θargmax​logP(X∣θ) 但是，有的时候，极大似然估计并不是很好用。核心问题在于观测数据 X \mathcal X X过于复杂。

如果观测数据 X \mathcal X X的分布简单，我们能够发现它的规律还好说，但如果观测数据的分布如下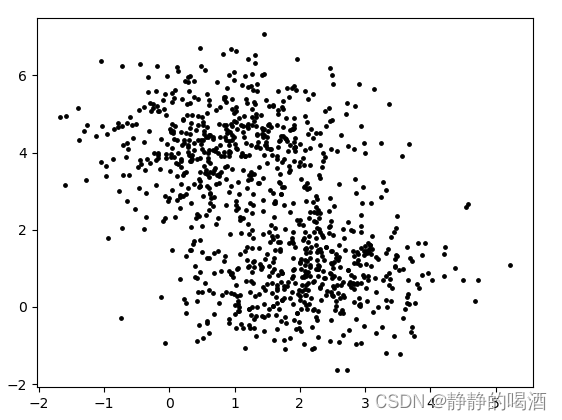： 在没有标签信息的条件下，当前这个 2维的观测数据的分布是比较复杂的。 可能存在 已经投入了足够多的样本，使用极大似然估计去估计模型参数 θ \theta θ收效甚微。

因此，我们可能需要对样本分布进行假设，即：假定观测数据 X \mathcal X X服从某个概率模型 P ( Z ) P(\mathcal Z) P(Z)，换句话说，通过概率模型 P ( Z ) P(\mathcal Z) P(Z)可以源源不断地生成观测数据 X \mathcal X X。 因而，复杂的样本分布 P ( X ) P(\mathcal X) P(X)可以通过两步走的形式迂回求解：

• 将隐变量 Z \mathcal Z Z引进来： P ( X , Z ) = P ( X ∣ Z ) P ( Z ) P(\mathcal X,\mathcal Z) = P(\mathcal X \mid \mathcal Z) P(\mathcal Z) P(X,Z)=P(X∣Z)P(Z)
• 用概率密度积分的方式将隐变量 Z \mathcal Z Z积分掉： P ( X ) = ∫ Z P ( X , Z ) d Z P(\mathcal X) = \int_{\mathcal Z} P(\mathcal X,\mathcal Z)d\mathcal Z P(X)=∫Z​P(X,Z)dZ 或者可以看成期望的形式： P ( X ) = E Z [ P ( X , Z ) ] P(\mathcal X) = \mathbb E_{\mathcal Z} \left[P(\mathcal X,\mathcal Z)\right] P(X)=EZ​[P(X,Z)] 这和EM算法的表示思想如出一辙： 上面两端各添个log就更像啦~ log ⁡ P ( X ∣ θ ) = E Z ∣ X , θ [ log ⁡ P ( X , Z ∣ θ ) ] \log P(\mathcal X \mid \theta) = \mathbb E_{\mathcal Z \mid \mathcal X,\theta} \left[\log P(\mathcal X,\mathcal Z \mid \theta)\right] logP(X∣θ)=EZ∣X,θ​[logP(X,Z∣θ)]

因此，引入隐变量 Z \mathcal Z Z的本质在于简化求解基于当前样本的概率分布 P ( X ) P(\mathcal X) P(X)。

相关参考： 机器学习-EM算法4-再回首