- 引言
- 回顾：隐马尔可夫模型
- 变量性质
- 模型参数
- 假设支撑
- 问题处理
- 总结与延伸
- HMM(动态模型)与GMM(静态模型)的联系
- 关于动态模型的问题延伸
上一节介绍了基于隐马尔可夫模型的解码问题，本节将针对之前介绍的关于隐马尔可夫模型的相关性质并延伸至动态模型的高度 进行总结。
回顾：隐马尔可夫模型 变量性质隐马尔可夫模型(Hidden Mixture Model,HMM)的概率图格式表示如下：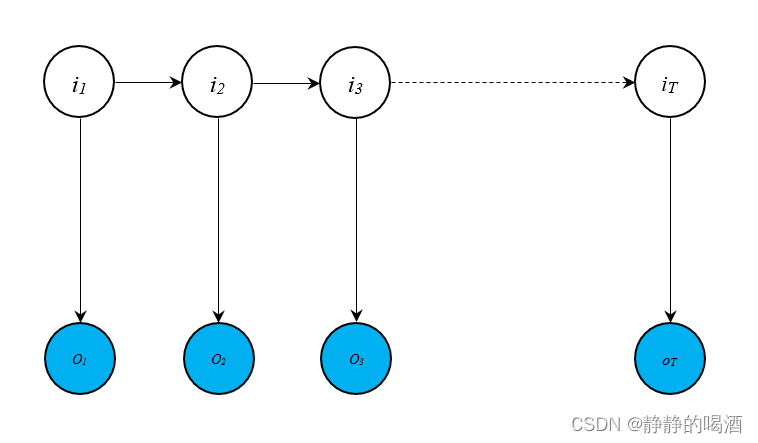 
从图中观察:
- 图像上方的节点被称为状态变量 i t ( t = 1 , 2 , ⋯ , T ) i_t(t = 1,2,\cdots,T) it(t=1,2,⋯,T)；图像下方的节点被称为观测变量 o t ( t = 1 , 2 , ⋯ , T ) o_t(t = 1,2,\cdots,T) ot(t=1,2,⋯,T)；
- 状态变量基于时间过程的有序排列而产生的序列称为状态序列；同理，观测变量基于时间过程的有序排列而产生的序列称为观测序列。记状态序列为 I \mathcal I I，观测序列为 O \mathcal O O，具体表示如下： I = ( i 1 , i 2 , ⋯ , i T ) O = ( o 1 , o 2 , ⋯ , o T ) \mathcal I = (i_1,i_2,\cdots,i_T) \\ \mathcal O = (o_1,o_2,\cdots,o_T) I=(i1,i2,⋯,iT)O=(o1,o2,⋯,oT)
基于隐马尔可夫模型的性质，状态序列 I \mathcal I I中的任一状态变量的取值结果均是离散的。即： ∀ i t ∈ I , i t ∈ Q = { q 1 , q 2 , ⋯ , q K } \forall i_t \in \mathcal I, \quad i_t \in \mathcal Q = \{q_1,q_2,\cdots,q_{\mathcal K}\} ∀it∈I,it∈Q={q1,q2,⋯,qK} 其中： q 1 , ⋯ , q K q_1,\cdots,q_{\mathcal K} q1,⋯,qK称为状态值， Q \mathcal Q Q称为状态值集合。同理，观测序列 O \mathcal O O中的任一观测变量的取值结果均是离散的。即： ∀ o t ∈ O , o t ∈ V = { v 1 , v 2 , ⋯ , v M } \forall o_t \in \mathcal O,\quad o_t \in \mathcal V = \{v_1,v_2,\cdots,v_{\mathcal M}\} ∀ot∈O,ot∈V={v1,v2,⋯,vM} 其中： v 1 , v 2 , ⋯ , v M v_1,v_2,\cdots,v_{\mathcal M} v1,v2,⋯,vM成为观测值， V \mathcal V V称为观测值集合。
模型参数隐马尔可夫模型的参数记作 λ \lambda λ，模型参数共包含三个部分：
- 初始概率分布 π \pi π： 即 状态变量 i 1 i_1 i1 选择任意状态值 q i ( i ∈ 1 , 2 , ⋯ , K ) q_i (i \in {1,2,\cdots,\mathcal K}) qi(i∈1,2,⋯,K)的概率结果组成的向量形式。即： π = [ P ( i 1 = q 1 ) P ( i 1 = q 2 ) ⋮ P ( i 1 = q K ) ] K × 1 ∑ k = 1 K P ( i 1 = q k ) = 1 \pi = \begin{bmatrix}P(i_1 = q_1) \\ P(i_1 = q_2) \\ \vdots \\ P(i_1 = q_{\mathcal K})\end{bmatrix}_{\mathcal K \times 1} \quad \sum_{k=1}^{\mathcal K} P(i_1 = q_{k}) = 1 π=⎣ ⎡P(i1=q1)P(i1=q2)⋮P(i1=qK)⎦ ⎤K×1k=1∑KP(i1=qk)=1
- 状态转移矩阵 A \mathcal A A：矩阵 A \mathcal A A中的任意一个元素 a i j a_{ij} aij表示当前时刻的状态变量 i t = q i i_t =q_i it=qi的条件下，下一时刻的状态变量 i t + 1 = q j i_{t+1} = q_j it+1=qj的后验概率结果。即： A = [ a i j ] K × K , a i j = P ( i t + 1 = q j ∣ i t = q i ) \mathcal A = [a_{ij}]_{\mathcal K \times \mathcal K},\quad a_{ij} = P(i_{t+1}=q_j \mid i_t = q_i) A=[aij]K×K,aij=P(it+1=qj∣it=qi)
- 发射矩阵 B \mathcal B B：矩阵中的任意一个元素 b j ( k ) b_{j}(k) bj(k)表示当前时刻的状态变量 i t = q i i_t =q_i it=qi的条件下，对应时刻的观测变量 o t = v k o_t = v_k ot=vk的后验概率结果。即： B = [ b j ( k ) ] K × M , b j ( k ) = P ( o t = v k ∣ i t = q j ) \mathcal B = [b_j(k)]_{\mathcal K \times \mathcal M}, \quad b_j(k) = P(o_t = v_k \mid i_t = q_j) B=[bj(k)]K×M,bj(k)=P(ot=vk∣it=qj)
- 齐次马尔可夫假设：任一时刻状态变量 i t i_t it的后验概率，只和其前一时刻的状态变量 i t − 1 i_{t-1} it−1相关，与其他变量无关。即： P ( i t ∣ i t − 1 , ⋯ , i 1 , o t − 1 , ⋯ , o 1 ) = P ( i t ∣ i t − 1 ) P(i_t \mid i_{t-1},\cdots,i_{1},o_{t-1},\cdots,o_1) = P(i_t \mid i_{t-1}) P(it∣it−1,⋯,i1,ot−1,⋯,o1)=P(it∣it−1)
- 观测独立性假设：任一时刻观测变量 o t o_t ot的后验概率，只和对应时刻的状态变量 i t i_t it相关，与其他变量无关。 P ( o t ∣ i t , i t − 1 , ⋯ , i 1 , o t − 1 , ⋯ , o 1 ) = P ( o t ∣ i t ) P(o_t \mid i_t,i_{t-1},\cdots,i_1,o_{t-1},\cdots,o_1) = P(o_t \mid i_t) P(ot∣it,it−1,⋯,i1,ot−1,⋯,o1)=P(ot∣it)
隐马尔可夫模型主要处理三类问题：
-
求值问题/评估问题(Evaluation)：其具体表述是：隐马尔可夫模型给定模型参数 λ = ( π , A , B ) \lambda = (\pi,\mathcal A,\mathcal B) λ=(π,A,B)，求解 观测序列 O = ( o 1 , o 2 , ⋯ , o T ) \mathcal O = (o_1,o_2,\cdots,o_T) O=(o1,o2,⋯,oT)的后验概率结果 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)。 常用的求解方式分为两种：
- 前向算法(Forward ALgorithm)：通过求解
P
(
o
1
,
⋯
,
o
t
,
i
t
=
q
i
∣
λ
)
P(o_1,\cdots,o_t,i_t=q_i \mid \lambda)
P(o1,⋯,ot,it=qi∣λ)和
P
(
o
1
,
⋯
,
o
t
+
1
,
i
t
+
1
=
q
j
∣
λ
)
P(o_1,\cdots,o_{t+1},i_{t+1} = q_j \mid \lambda)
P(o1,⋯,ot+1,it+1=qj∣λ)之间的关联关系，迭代求解
P
(
O
∣
λ
)
P(\mathcal O \mid \lambda)
P(O∣λ)：
从α 1 ( i ) \alpha_1(i) α1(i)开始，经过T T T次迭代，即可求出对应结果α T ( i ) \alpha_T(i) αT(i); α t ( i ) = P ( o 1 , ⋯ , o t , i t = q i ∣ λ ) α t + 1 ( j ) = P ( o 1 , ⋯ , o t + 1 , i t + 1 = q j ∣ λ ) α t + 1 ( j ) = ∑ i = 1 K b j ( o t + 1 ) ⋅ a i j ⋅ α t ( i ) P ( O ∣ λ ) = ∑ i = 1 K α T ( i ) \alpha_t(i) = P(o_1,\cdots,o_t,i_t=q_i \mid \lambda) \\ \alpha_{t+1}(j) = P(o_1,\cdots,o_{t+1},i_{t+1} = q_j \mid \lambda) \\ \alpha_{t+1}(j) = \sum_{i=1}^{\mathcal K} b_j(o_{t+1})\cdot a_{ij}\cdot \alpha_t(i) \\ P(\mathcal O \mid \lambda) = \sum_{i=1}^{\mathcal K}\alpha_T(i) αt(i)=P(o1,⋯,ot,it=qi∣λ)αt+1(j)=P(o1,⋯,ot+1,it+1=qj∣λ)αt+1(j)=i=1∑Kbj(ot+1)⋅aij⋅αt(i)P(O∣λ)=i=1∑KαT(i) - 后向算法(Backward Algorithm)：通过求解条件概率
P
(
o
t
+
1
,
⋯
,
o
T
∣
i
t
=
q
i
,
λ
)
P(o_{t+1},\cdots,o_{T} \mid i_t = q_i,\lambda)
P(ot+1,⋯,oT∣it=qi,λ)和条件概率
P
(
o
t
,
⋯
,
o
T
∣
i
t
−
1
=
q
j
,
λ
)
P(o_t,\cdots,o_T \mid i_{t-1} = q_j,\lambda)
P(ot,⋯,oT∣it−1=qj,λ)之间的关联关系，迭代求解
P
(
O
∣
λ
)
P(\mathcal O \mid \lambda)
P(O∣λ)：
与前向算法相反，从β T ( i ) \beta_T(i) βT(i)开始，经过T T T次迭代，即可求出对应结果β 1 ( j ) \beta_1(j) β1(j); β t ( i ) = P ( o t + 1 , ⋯ , o T ∣ i t = q i , λ ) β t − 1 ( j ) = P ( o t , ⋯ , o T ∣ i t − 1 = q j , λ ) β t − 1 ( j ) = ∑ i = 1 K b i ( o t ) ⋅ β t ( i ) ⋅ a i j P ( O ∣ λ ) = ∑ i = 1 K [ b i ( o t ) ⋅ β 1 ( i ) ⋅ π ] \beta_t(i) = P(o_{t+1},\cdots,o_{T} \mid i_t = q_i,\lambda) \\ \beta_{t-1}(j) = P(o_t,\cdots,o_T \mid i_{t-1} = q_j,\lambda) \\ \beta_{t-1}(j) = \sum_{i=1}^{\mathcal K} b_i(o_t) \cdot \beta_t(i) \cdot a_{ij} \\ P(\mathcal O \mid \lambda) = \sum_{i=1}^{\mathcal K} [b_i(o_t) \cdot \beta_1(i) \cdot \pi] βt(i)=P(ot+1,⋯,oT∣it=qi,λ)βt−1(j)=P(ot,⋯,oT∣it−1=qj,λ)βt−1(j)=i=1∑Kbi(ot)⋅βt(i)⋅aijP(O∣λ)=i=1∑K[bi(ot)⋅β1(i)⋅π]
- 前向算法(Forward ALgorithm)：通过求解
P
(
o
1
,
⋯
,
o
t
,
i
t
=
q
i
∣
λ
)
P(o_1,\cdots,o_t,i_t=q_i \mid \lambda)
P(o1,⋯,ot,it=qi∣λ)和
P
(
o
1
,
⋯
,
o
t
+
1
,
i
t
+
1
=
q
j
∣
λ
)
P(o_1,\cdots,o_{t+1},i_{t+1} = q_j \mid \lambda)
P(o1,⋯,ot+1,it+1=qj∣λ)之间的关联关系，迭代求解
P
(
O
∣
λ
)
P(\mathcal O \mid \lambda)
P(O∣λ)：
-
学习问题/参数求解问题(Learning) 针对模型参数 λ \lambda λ的求解问题，采用狭义EM算法迭代求解： λ ( t + 1 ) = arg max λ ∑ I [ log P ( O ∣ λ ) ⋅ P ( I ∣ O , λ ( t ) ) ] \lambda^{(t+1)} = \mathop{\arg\max}\limits_{\lambda} \sum_{\mathcal I} \left[\log P(\mathcal O \mid \lambda) \cdot P(\mathcal I \mid \mathcal O,\lambda^{(t)}) \right] λ(t+1)=λargmaxI∑[logP(O∣λ)⋅P(I∣O,λ(t))] 以求解 λ ( t + 1 ) \lambda^{(t+1)} λ(t+1)中的 π ( t + 1 ) \pi^{(t+1)} π(t+1)为例，已知上时刻迭代的求解结果 λ ( t ) \lambda^{(t)} λ(t)， π ( t + 1 ) \pi^{(t+1)} π(t+1)使用 λ ( t ) \lambda^{(t)} λ(t)表示如下： π ( t + 1 ) = ( π 1 ( t + 1 ) , π 2 ( t + 1 ) , ⋯ , π K ( t + 1 ) ) π k ( t + 1 ) = P ^ ( i 1 = q k ) = P ( O , i 1 = q k ∣ λ ( t ) ) P ( O ∣ λ ( t ) ) ( k = 1 , 2 , ⋯ , K ) \pi^{(t+1)} = (\pi_1^{(t+1)},\pi_2^{(t+1)},\cdots,\pi_{\mathcal K}^{(t+1)}) \\ \pi_k^{(t+1)} = \hat P(i_1 = q_k) = \frac{P(\mathcal O,i_1 = q_k \mid \lambda^{(t)})}{P(\mathcal O \mid \lambda^{(t)})} \quad (k=1,2,\cdots,\mathcal K) π(t+1)=(π1(t+1),π2(t+1),⋯,πK(t+1))πk(t+1)=P^(i1=qk)=P(O∣λ(t))P(O,i1=qk∣λ(t))(k=1,2,⋯,K)
-
解码问题(Decoding) 解码问题被看做 给定长度为 T T T的观测序列 O = ( o 1 , o 2 , ⋯ , o T ) \mathcal O = (o_1,o_2,\cdots,o_T) O=(o1,o2,⋯,oT)，目标是求解与观测序列 O \mathcal O O对应状态序列 I = ( i 1 , i 2 , ⋯ , i T ) \mathcal I = (i_1,i_2,\cdots,i_T) I=(i1,i2,⋯,iT)的后验概率 P ( I ∣ O ) P(\mathcal I \mid \mathcal O) P(I∣O)： 常用方法是维特比算法(Viterbi)，其核心是 分别给定 t t t时刻状态变量 i t = q i i_t = q_i it=qi与 t + 1 t+1 t+1时刻状态变量 i t + 1 = q j i_{t+1}=q_j it+1=qj，并分别求解从初始状态 i 1 i_1 i1开始，到 i t , i t + 1 i_{t},i_{t+1} it,it+1的最大联合概率，并找出他们之间的关系： δ t ( k ) = max i 1 , i 2 , ⋯ , i t − 1 P ( o 1 , ⋯ , o t , i 1 , ⋯ , i t − 1 , i t = q i ∣ λ ) δ t + 1 ( j ) = max i 1 , i 2 , ⋯ , i t P ( o 1 , ⋯ , o t + 1 , i 1 , ⋯ , i t , i t + 1 = q j ∣ λ ) δ t + 1 ( j ) = max a ≤ k ≤ K [ δ t ( k ) ⋅ a k j ⋅ b i ( o t + 1 ) ] \delta_t(k) = \mathop{\max}\limits_{i_1,i_2,\cdots,i_{t-1}} P(o_1,\cdots,o_t,i_1,\cdots,i_{t-1},i_t = q_i \mid \lambda) \\ \delta_{t+1}(j) = \mathop{\max}\limits_{i_1,i_2,\cdots,i_{t}} P(o_1,\cdots,o_{t+1},i_1,\cdots,i_t,i_{t+1} = q_j \mid \lambda) \\ \delta_{t+1}(j) = \max_{a \leq k\leq\mathcal K} [\delta_t(k) \cdot a_{kj} \cdot b_i(o_{t+1})] δt(k)=i1,i2,⋯,it−1maxP(o1,⋯,ot,i1,⋯,it−1,it=qi∣λ)δt+1(j)=i1,i2,⋯,itmaxP(o1,⋯,ot+1,i1,⋯,it,it+1=qj∣λ)δt+1(j)=a≤k≤Kmax[δt(k)⋅akj⋅bi(ot+1)] 基于上述迭代关系，从初始状态 i 1 i_1 i1开始，查找转移过程中的最优状态变量： ϕ t + 1 ( j ) = arg max 1 ≤ k ≤ K [ δ t ( k ) ⋅ a k j ⋅ b i ( o t + 1 ) ] \phi_{t+1}(j) = \mathop{\arg\max}\limits_{1 \leq k \leq \mathcal K}[\delta_t(k) \cdot a_{kj} \cdot b_i(o_{t+1})] ϕt+1(j)=1≤k≤Kargmax[δt(k)⋅akj⋅bi(ot+1)] 从而得到基于状态值的下标序列： ( ϕ 1 , ϕ 2 , ⋯ , ϕ T ) (\phi_1,\phi_2,\cdots,\phi_T) (ϕ1,ϕ2,⋯,ϕT)
首先，隐马尔可夫模型是一种包含隐变量的概率图模型，并且它是一种动态模型(Dynamic Model)：
- 本身是一个混合模型(Mixture Model)；
- 信息随着时间的变化而变化；
这里的时间也可以是‘抽象的时间概念，如序列’。
如果从混合模型的角度观察，在之前介绍的高斯混合模型(Gaussian Mixture Model,GMM)，它的概率图模型如下所示：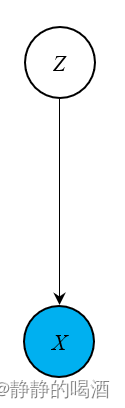 
其中隐变量
Z
\mathcal Z
Z服从离散分布：
∑ i = 1 K p i = 1 \sum_{i=1}^{\mathcal K} p_i = 1 i=1∑Kpi=1 如果使用隐马尔可夫模型中的表达方式，状态变量 Z \mathcal Z Z确定 的条件下，观测变量 X \mathcal X X的概率分布，即 发射分布(与离散的发射矩阵相对应) 服从高斯分布。
我们在介绍隐马尔可夫模型时，仅强调了状态变量
i
t
∈
I
i_t \in \mathcal I
it∈I 的取值范围是 离散的，对观测变量
o
t
∈
O
o_t \in \mathcal O
ot∈O的发射概率
P
(
o
t
∣
i
t
)
P(o_t \mid i_t)
P(ot∣it)没有这种约束； 在公式推导过程中，为了简化运算，将观测变量也设置为离散的形式。
因此，如果设隐马尔可夫模型中
P
(
o
t
∣
i
t
)
∼
N
(
μ
t
,
Σ
t
)
P(o_t \mid i_t) \sim \mathcal N(\mu_t,\Sigma_t)
P(ot∣it)∼N(μt,Σt)，那么，该隐马尔可夫模型就可以看成 高斯混合模型 + 时间(序列)信息 的形式。其转移过程如下图所示：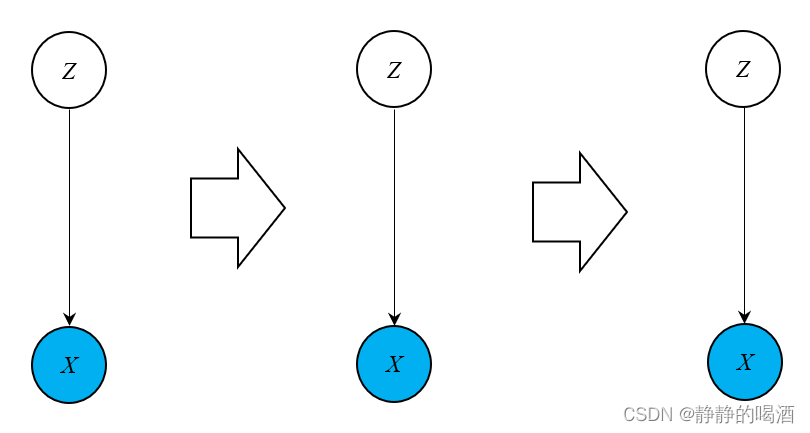 
基于上述隐马尔可夫模型的问题处理，我们将其延伸到动态模型(状态空间模型)(State-Space Mdoel)的高度，对 动态模型的问题处理进行概括： 补概率图的坑~
-
学习问题/模型参数求解问题(Learning)：通过可观测的样本数据 X \mathcal X X，学习概率模型 P ( X ∣ θ ) P(\mathcal X \mid \theta) P(X∣θ)中的参数 θ \theta θ。
-
推断问题(Inference)：通过可观测的样本数据 X \mathcal X X，推断概率模型中隐变量的后验概率 P ( Z ∣ X , θ ) P(\mathcal Z \mid \mathcal X,\theta) P(Z∣X,θ)。
基于状态空间模型： X = ( x 1 , x 2 , ⋯ , x T ) Z = ( z 1 , z 2 , ⋯ , z T ) \mathcal X = (x_1,x_2,\cdots,x_T) \\ \mathcal Z = (z_1,z_2,\cdots,z_T) X=(x1,x2,⋯,xT)Z=(z1,z2,⋯,zT) 并且各观测数据之间不是独立同分布关系： x i ⇎ i.i.d x j i , j ∈ { 1 , 2 , ⋯ , T } ; i ≠ j x_i \overset{\text{i.i.d}}{\nLeftrightarrow} x_j \quad i,j \in \{1,2,\cdots,T\};i \neq j xi⇎i.i.dxji,j∈{1,2,⋯,T};i=j 针对状态空间模型，它的推断问题根据不同的求解要求进行详细划分：
-
解码问题(Decoding)： 给定 长度为 t t t的观测序列 X = ( x 1 , ⋯ , x t ) \mathcal X = (x_1,\cdots,x_t) X=(x1,⋯,xt)，求解 对应时刻隐状态序列 Z = ( z 1 , ⋯ , z t ) \mathcal Z = (z_1,\cdots,z_t) Z=(z1,⋯,zt)的后验概率分布： P ( z 1 , ⋯ , z t ∣ x 1 , ⋯ , x t , θ ) P(z_1,\cdots,z_t \mid x_1,\cdots,x_t,\theta) P(z1,⋯,zt∣x1,⋯,xt,θ)
-
似然问题(Probability of Evidence) 如果模型只是一个普通的混合模型，而不是状态空间模型，如高斯混合模型，它的似然 P ( X ∣ θ ) P(\mathcal X \mid \theta) P(X∣θ)可以直接使用如下方式求解： P ( X ∣ θ ) = ∫ Z P ( X , Z ∣ θ ) d Z = ∫ Z P ( Z ∣ X , θ ) ⋅ P ( X ∣ Z , θ ) d Z \begin{aligned} P(\mathcal X \mid \theta) & = \int_{\mathcal Z} P(\mathcal X,\mathcal Z \mid \theta)d\mathcal Z \\ & = \int_{\mathcal Z} P(\mathcal Z \mid \mathcal X,\theta) \cdot P(\mathcal X \mid \mathcal Z,\theta) d\mathcal Z \end{aligned} P(X∣θ)=∫ZP(X,Z∣θ)dZ=∫ZP(Z∣X,θ)⋅P(X∣Z,θ)dZ 而状态空间模型需要求解观测序列 X \mathcal X X中各时刻观测变量 x t x_t xt联合概率分布的似然结果： P ( X ∣ θ ) = P ( x 1 , x 2 , ⋯ , x T ∣ θ ) P(\mathcal X \mid \theta) = P(x_1,x_2,\cdots,x_T \mid \theta) P(X∣θ)=P(x1,x2,⋯,xT∣θ)
-
滤波问题(Filtering) 给定从初始时刻到 t t t时刻的观测序列 ( x 1 , x 2 , ⋯ , x t ) (x_1,x_2,\cdots,x_t) (x1,x2,⋯,xt)，求解 t t t时刻状态变量的后验概率分布：
对t t t时刻状态变量P ( z t ) P(z_t) P(zt)进行估计时，可能并不是仅和'对应观测变量'x t x_t xt相关，而是和之前时刻的观测变量( x 1 , ⋯ , x t ) (x_1,\cdots,x_t) (x1,⋯,xt)可能存在关系。因此，滤波(Filtering)的含义是指P ( z t ∣ x 1 , ⋯ , x t ) P(z_t \mid x_1,\cdots,x_t) P(zt∣x1,⋯,xt)可能比P ( z t ∣ x t ) P(z_t \mid x_t) P(zt∣xt)更加准确，过滤掉更多的噪声。P ( z t ∣ x 1 , ⋯ , x t ) P(z_t \mid x_1,\cdots,x_t) P(zt∣x1,⋯,xt) 因此，滤波问题常适用于在线学习方法中。在线学习(On-line Learning)：一次输入一条数据，该数据训练完毕后直接更新权重。因此，它不需要一开始就提供完整的训练数据集； 在线学习的缺点也很明显，由于一条一条训练，模型参数更新过程可能随着加入的错误数据导致更新方向偏移；
离线学习(Off-line Learning)：一开始提供一个数据集，划分成 m m m个batch块，至少训练一个batch块再更新数据。 这种方式可以弥补在线学习的缺陷，一次性投入若干样本进行训练，不会因为个别错误数据使模型参数偏移的过于严重。
-
平滑问题(Smoothing) 给定一个完整的观测序列 ( x 1 , x 2 , ⋯ , x T ) (x_1,x_2,\cdots,x_T) (x1,x2,⋯,xT)，求解 t t t时刻的状态变量 z t z_t zt。即： P ( z t ∣ x 1 , x 2 , ⋯ , x T ) P(z_t \mid x_1,x_2,\cdots,x_T) P(zt∣x1,x2,⋯,xT) 这种操作通常对应离线学习。已经有了完整数据，对某一部分参数进行复盘。
-
预测问题(Prediction) 在 隐马尔可夫模型——解码问题提到过预测问题。
情况1：给定初始时刻到 t t t时刻的观测序列 ( x 1 , x 2 , ⋯ , x t ) (x_1,x_2,\cdots,x_t) (x1,x2,⋯,xt)，求解 后续时刻的状态变量： P ( z t + 1 ∣ x 1 , ⋯ , x t ) P(z_{t+1} \mid x_1,\cdots,x_t) P(zt+1∣x1,⋯,xt) 并不一定只求解后续一个时刻的状态变量，预测后续若干时刻的联合概率分布 也属于预测问题的求解范围。
以后续两个状态变量z t + 1 , z t + 2 z_{t+1},z_{t+2} zt+1,zt+2为例。P ( z t + 1 , z t + 2 ∣ x 1 , x 2 , ⋯ , x t ) P(z_{t+1},z_{t+2} \mid x_1,x_2,\cdots,x_t) P(zt+1,zt+2∣x1,x2,⋯,xt) 情况2：给定初始时刻到 t t t时刻的观测序列 ( x 1 , x 2 , ⋯ , x t ) (x_1,x_2,\cdots,x_t) (x1,x2,⋯,xt)，求解后续时刻的观测变量：同上，以后续两个观测变量x t + 1 , x t + 2 x_{t+1},x_{t+2} xt+1,xt+2为例。P ( x t + 1 , x t + 2 ∣ x 1 , x 2 , ⋯ , x t ) P(x_{t+1},x_{t+2} \mid x_1,x_2,\cdots,x_t) P(xt+1,xt+2∣x1,x2,⋯,xt)
-
相关参考： Deep Learning | 机器学习中的在线学习和离线学习 区别 机器学习-隐马尔可夫模型7-小结-Filtering&Smoothing&Prediction (1)
