博弈论 详解

😊 | Powered By HeartFireY | Game 一、博弈论简介

博弈论 ，是经济学的一个分支，主要研究具有竞争或对抗性质的对象，在一定规则下产生的各种行为。博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。

通俗地讲，博弈论主要研究的是：在一个游戏中，进行游戏的多位玩家的策略。

对于算法竞赛中的博弈问题，一般具有以下特征：

• 博弈模型为两人轮流决策的非合作博弈。即两人轮流进行决策，并且两人都使用最优策略来获取胜利。
• 博弈是有限的。即无论两人怎样决策，都会在有限步后决出胜负。
• 公平博弈。即两人进行决策所遵循的规则相同。

二、基本概念 1.公平组合游戏

公平组合游戏的定义如下：

• 游戏有两个人参与，二者轮流做出决策，双方均知道游戏的完整信息；
• 任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关，而与游戏者无关；
• 游戏中的同一个状态不可能多次抵达，游戏以玩家无法行动为结束，且游戏一定会在有限步后以非平局结束。

大部分的棋类游戏都 不是 公平组合游戏，如国际象棋、中国象棋、围棋、五子棋等（因为双方都不能使用对方的棋子）。

公平游戏具有一个重要的性质：

如果一个游戏者能够讲状态A变为状态B，那么另外一个游戏者必然也能实现这样的操作。

2.博弈图和状态 1).博弈图

如果将每个状态视为一个节点，再从每个状态向它的后继状态连边，我们就可以得到一个博弈状态图。

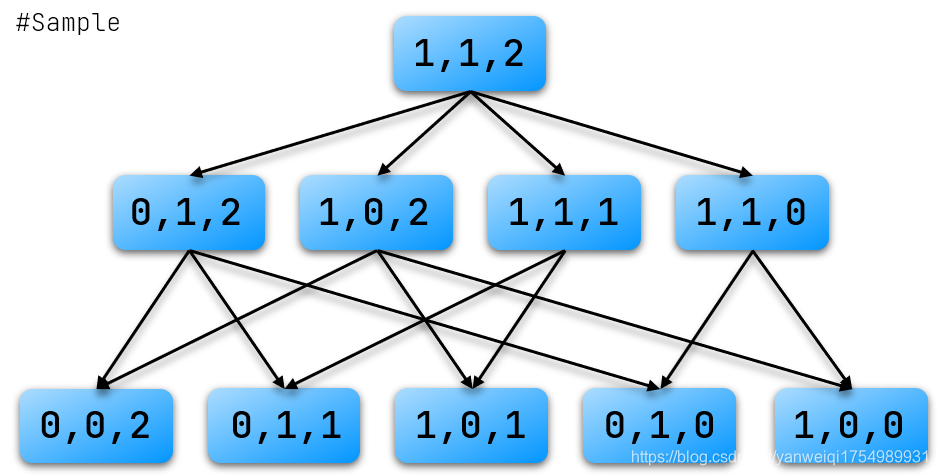
如上图，我们假定存在博弈状态 ( i ,   j ,   k ) (i,\ j,\ k) (i, j, k)，表示局面为 ( i ,   j ,   k ) (i,\ j,\ k) (i, j, k)的状态，则我们可以根据状态的转移确定博弈图。

易知：博弈图必为DAG(有向无环图)。

2).状态

我们首先定义博弈中常用的两种状态：必胜态、必输态

1. 必胜态：先手必胜的状态
2. 必败态：先手必败的状态

同时我们对决策局面进行定义：

1. **P局面：**即为Previous-position，上次移动的人具有必胜策略的局面(先手必败)。
   • 任何无法移动的局面都是P局面
2. **N局面：**即为Next-position，当前移动的人具有必胜决策的场面(先手必胜)。
   • 可以移动到P局面的局面是N局面
   • 所有移动都导致移动到N局面的局面是P局面

有了状态的定义，对于博弈图中的状态点我们可以继续定义：

1. P点：必败点，某玩家位于此点，只要对方无失误，则必败
2. N点：必胜点，某玩家位于此点，只要自己无失误，则必胜

通过推理，我们可以得到以下三条定理：

• 定理 1：没有后继状态的状态是必败状态。(终止状态必为**P局面**)
• 定理 2：一个状态是必胜状态当且仅当存在至少一个必败状态为它的后继状态。(N局面的下一步中有一个是P局面)
• 定理 3：一个状态是必败状态当且仅当它的所有后继状态均为必胜状态。(P局面的下一步全部是**N局面**)

直接这样阐述有些难以理解，我们继续进行解释：

对于定理 1，如果游戏进行不下去了，那么这个玩家就输掉了游戏。对于这个状态是十分容易理解的–大多数游戏在此时已经无法继续进行(终结局面)，比如N堆石子任意取游戏，当N堆石子均为空时不会再出现任何的后继状态，此时的状态为必胜状态；

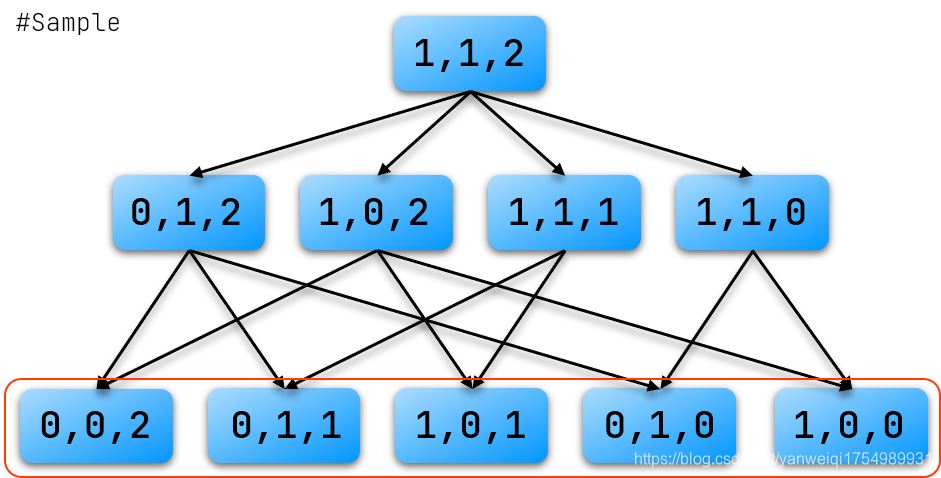
如图，红框内所示的状态点全部为“终结局面”

对于定理 2，如果该状态至少有一个后继状态为必败状态，那么玩家可以通过操作到该必败状态；此时对手的状态为必败状态——对手必定是失败的，而相反地，自己就获得了胜利。

换句话说，对于公平游戏而言，只有让对手走到必败状态，自己才能赢

对于定理 3，如果不存在一个后继状态为必败状态，那么无论如何，玩家只能操作到必胜状态；此时对手的状态为必胜状态——对手必定是胜利的，自己就输掉了游戏。

换句话说，你能到达必胜点且无法向必败点转移，那么你的对手也能到必胜点，这样你就输了。

如果博弈图是一个有向无环图，则通过这三个定理，我们可以在绘出博弈图的情况下用 O ( N + M ) O(N+M) O(N+M) 的时间（其中 N N N 为状态种数， M M M 为边数）得出每个状态是必胜状态还是必败状态。

三、博弈模型 1.巴什博弈

巴什博弈属于基本的博弈问题，其典型特征为：

给定 n n n堆物品，两个人轮流从这堆物品中取物品，规定每次最少取 1 1 1个，最多取 m m m个，最后取光者为胜。

当 n = m + 1 n = m + 1 n=m+1时，由于一次最多只能取 m m m个，所以无论先取者拿走多少个，后取者都能一次拿走剩余的物品，后取者取胜；

所以当一方面对的局势为 n = ( m + 1 ) × r + s n = (m + 1) \times r + s n=(m+1)×r+s（其中 r r r为任意自然数， s ≤ m s \leq m s≤m)，如果先取者要取走 s s s个物品，如果后取者取走 x ( x ≤ m ) x(x \leq m) x(x≤m)个，那么后取者只要取走 m + 1 − k m + 1 - k m+1−k个，结果剩下 ( m − 1 ) ( r − 1 ) (m - 1)(r - 1) (m−1)(r−1)个，以后保持这样的取法，那么先取者肯定获胜，总之，要保持给对手留下 ( m + 1 ) (m + 1) (m+1)的倍数，就能最后获胜。

结论1：若 ( m + 1 ) ∣ n (m + 1) | n (m+1)∣n，则先手必败，否则先手必赢

一种常见的变形是“问题改为最后取光的人输”。那么此时的结论：

结论2：当 ( n − 1 ) % ( m + 1 ) = = 0 (n-1)\%(m + 1)==0 (n−1)%(m+1)==0时先手必输。

2.威佐夫博弈

威佐夫博弈问题具有的典型特征是：

有两堆各若干个物品，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

如何解决威佐夫博弈问题？

首先，我们定义 ( a i , b i )   ( a i ≤ b i , i = 1 , 2 , . . . , n ) (a_i, b_i) \ (a_i \leq b_i, i = 1, 2, ..., n) (ai​,bi​) (ai​≤bi​,i=1,2,...,n)表示两堆物品的数量并称其为局势，如果甲面对 ( 0 , 0 ) (0, 0) (0,0)，那么甲已经输了，这种局势我们称为奇异局势。前几个奇异局势，前几个奇异局势为 ( 0 , 0 ) 、 ( 1 , 2 ) 、 ( 3 , 5 ) 、 ( 4 , 7 ) 、 ( 6 , 10 ) 、 ( 8 , 13 ) 、 ( 9 , 15 ) 、 ( 11 , 18 ) 、 ( 12 , 20 ) (0, 0) 、(1, 2)、(3, 5)、(4, 7)、(6, 10)、(8, 13)、(9, 15)、(11, 18)、(12,20) (0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)。任意给定一个局势 ( a , b ) (a, b) (a,b)，如下公式可以判断其是否为奇异局势： a k = ⌊ k × ( 1 + 5 ) 2 ⌋ ,   b k = a k + k   ( k = 0 , 1 , 2 , . . . , n ) a_k = \lfloor \frac {k \times (1 + \sqrt{5})}{2} \rfloor, \ b_k = a_k + k \ (k = 0, 1, 2, ..., n) ak​=⌊2k×(1+5 ​)​⌋, bk​=ak​+k (k=0,1,2,...,n) 面对非奇异局势，先手必胜；面对奇异局势，先手必败。

满足上述公式的局势性质：

我们定义 ( x , y ) (x, y) (x,y)为第 k k k个奇异局势。

(1).任何自然数都包含在一个且仅有一个奇异局势中；

(2). x x x为前 1... k 1...k 1...k个奇异局势中没有出现过的最小正整数， y = x + k y = x + k y=x+k；

(3).任何操作都会将奇异局势转化为非奇异局势；

(4).可以采取适当的方法将非奇异局势转化为奇异局势。

我们对以上的分析进行总结，可以得出威佐夫博弈的通解形式：

对于给定的两堆石子 ( x , y )   ( x < y ) (x, y) \ (x < y) (x,y) (x b [ k ] a = a[k] ，b > b[k] a=a[k]，b>b[k] ,那么，取走 b − b [ k ] b - b[k] b−b[k]个物体，即变为奇异局势； 如果 a = a [ k ] ， b < b [ k ] a = a[k] ， b < b[k] a=a[k]，b a [ k ] ， b = a [ k ] + k a > a[k] ，b= a[k] + k a>a[k]，b=a[k]+k 则从第一堆中拿走多余的数量 a − a [ k ] a - a[k] a−a[k] 即可； 如果 a < a [ k ] ， b = a [ k ] + k a < a[k] ，b= a[k] + k a