数据结构 线段树--权值线段树 详解

😊 | Powered By HeartFireY | Weighted Segment Tree 一、权值线段树 简介 1.线段树

线段树是一种用于维护区间信息的高效数据结构，可以在 O ( log ⁡ N ) O(\log N) O(logN) 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

线段树维护的信息必须满足可加性，即能以可以接受的速度合并信息和修改信息，包括在使用Lazy标记时，标记也要满足可加性

具体有关线段树的的讲解请参考博客：线段树 详解与模板

2.权值线段树

权值线段树是一种建立在基本线段树之上的数据结构。因此它的基本原理仍是基于对区间的维护操作。但与线段树相区分的点是：权值线段树维护的信息与基本线段树有所差异：

• 基本线段树中每个系欸但用来维护一段区间的最大值或总和等；
• 权值线段树每个结点维护的是一个区间的数出现的次数。

实际上，权值线段树可以看作是一个桶，桶的操作它都支持，并且能够以更快的方式去完成。

根据权值线段树的性质，我们可以知道其主要用途：

权值线段树一般用于维护一段区间的数出现的次数，从它的定义来看，它可以快速计算出一段区间的数的出现次数。

在实际应用中，我们使用权值线段树查询区间第 K K K大的值。

二、权值线段树的基本原理与操作 1.权值线段树维护信息的原理

基础线段树和权值线段树的一个较大的区别点在于：(此处特指使用数组储存树结构)基础线段树根据初始的一个序列建立树结构，具有单独的建树操作；而权值线段树不需要进行建树操作，初始状态下默认建立一棵所有点权为 0 0 0的空树，对于每个元素，在遍历的时候相应的结点做自增运算。换而言之：

• 权值线段是一棵已经建好的线段树，储存树结构的下标范围根据区间最大值最小值确定(一般开大空间即可)；
• 初始状态下所有的点权均为 0 0 0；
• 执行插入元素的操作时，会导致插入值 v v v对应的 A [ v ] + + A[v]++ A[v]++，同时引发单点更新操作。
• 可以从上述描述中得到基本推论：向空的权值线段树中插入一个无序序列，则插入完成后在树上无法再得到原序列的遍历，但能通过遍历得到有序序列(无序序列变有序序列)

我们可以通过结构对比线段树与权值线段树的区别，以此理解原理。

我们给定序列 { 1 , 2 , 2 , 3 , 3 , 3 , 4 , 4 , 4 , 4 } \{1, 2, 2, 3, 3, 3, 4, 4, 4, 4 \} {1,2,2,3,3,3,4,4,4,4}，以该序列为例建立两种线段树。

首先，序列长度为 10 10 10，建立基础区间和查询线段树，结构图如下：

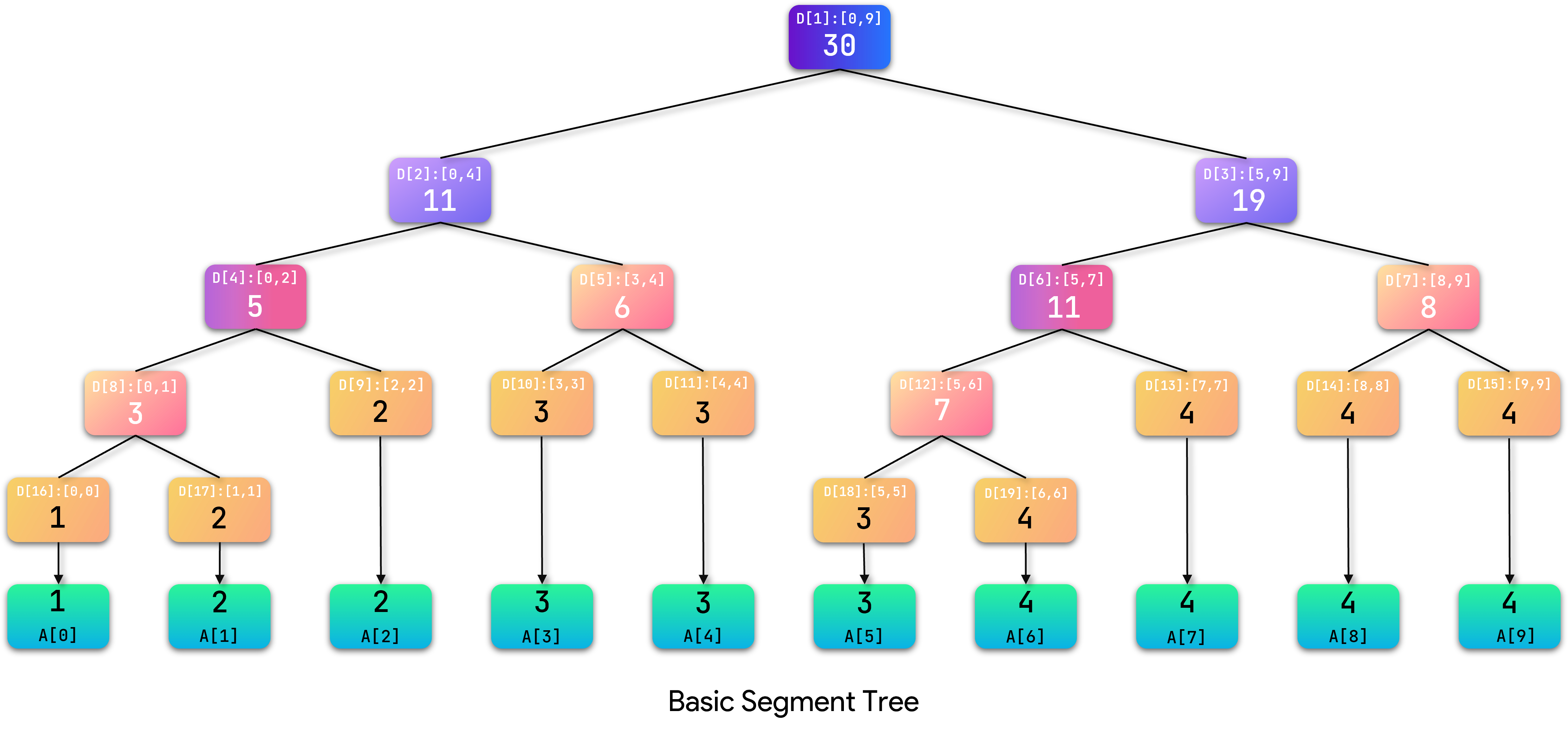
对应具体的细节不再阐述。我们继续建立权值线段树：首先给出一棵空树：

(注：为演示方便，A数组下标做+1操作，树上的范围也对应变化，这里懒得改了~)

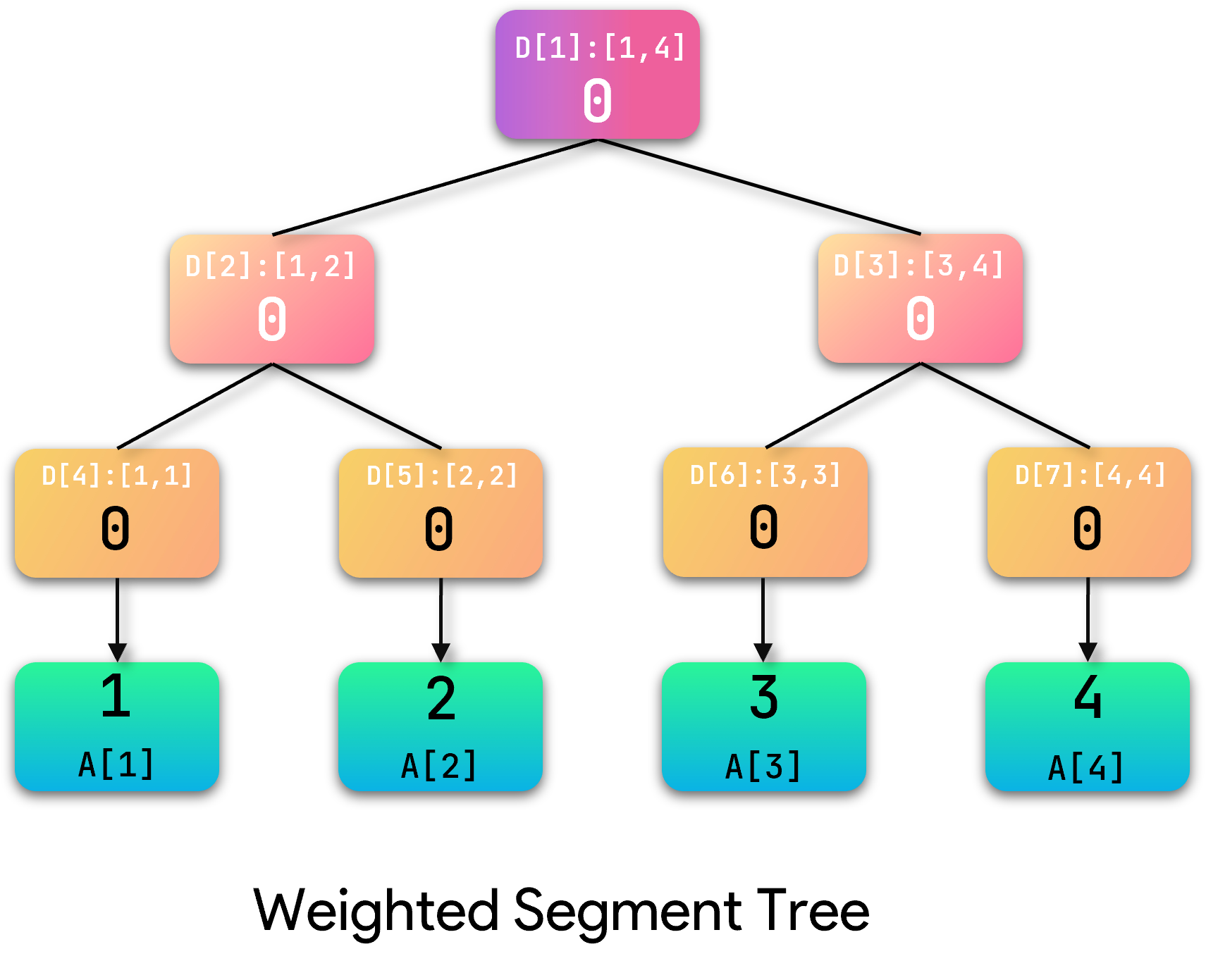
然后按照序列顺序插入元素：

解释：

A [ 1 ] = 1 A[1] = 1 A[1]=1：原序列中存在值为 1 1 1的元素 1 1 1个 A [ 2 ] = 1 A[2] = 1 A[2]=1：原序列中存在值为 2 2 2的元素 2 2 2个 A [ 3 ] = 1 A[3] = 1 A[3]=1：原序列中存在值为 3 3 3的元素 3 3 3个 A [ 4 ] = 1 A[4] = 1 A[4]=1：原序列中存在值为 4 4 4的元素 4 4 4个

D [ k ] D[k] D[k]：一定区间内所含元素的个数

我们继续探究查找第 K K K大元素的方法：

由于权值线段树每个节点记录了某段区间内包含的元素个数，且元素在叶子节点构成的序列中是有序的：

• 对于整列数中第 K K K大/小的值，我们从根节点开始判断（这里按第 K K K大为例），如果 K K K比右儿子大，就说明第 K K K大的数在左儿子所表示的值域中。然后， K K K要减去右儿子。（这是因为继续递归下去的时候，正确答案，整个区间的第 K K K大已经不再是左儿子表示区间的第 K K K大了)。如此递归到叶子节点时即为答案。
• 整棵线段树的根节点就表示整个值域有几个数。

我们很容易看出：在权值线段树中，采用元素到下标数组映射的方式进行插入。这样会导致一个问题：在数据离散程度较大的情况下，空间的利用效率比较低。因此我们对于线段树所开空间不足时，常采用离散化的方式进行解决。

📕 | 此处的前导知识：离散化(具体的参见离散化的讲解) 2.权值线段树的基本操作与实现 ①.查询第 K K K大/小元素

假设 K = 5 K = 5 K=5，那么查询过程是怎样的？

首先我们从根节点出发，由于要查询第 K K K大，是相对于终点而言的，因此从右子结点开始判断：

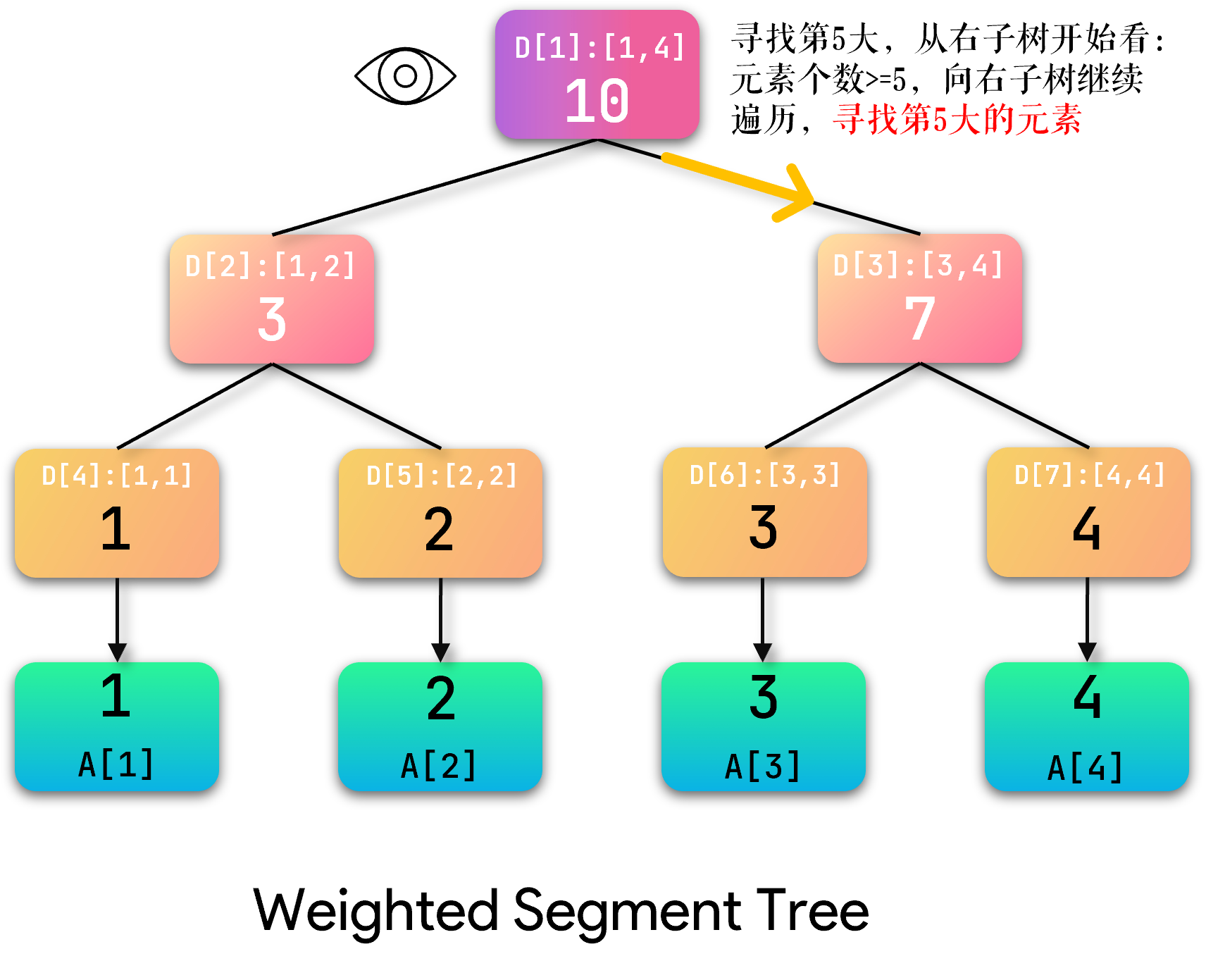
当前节点右子树包含 4 4 4个元素，所以应该向左子树遍历，注意：此时应该减去右子树的 4 4 4个元素！

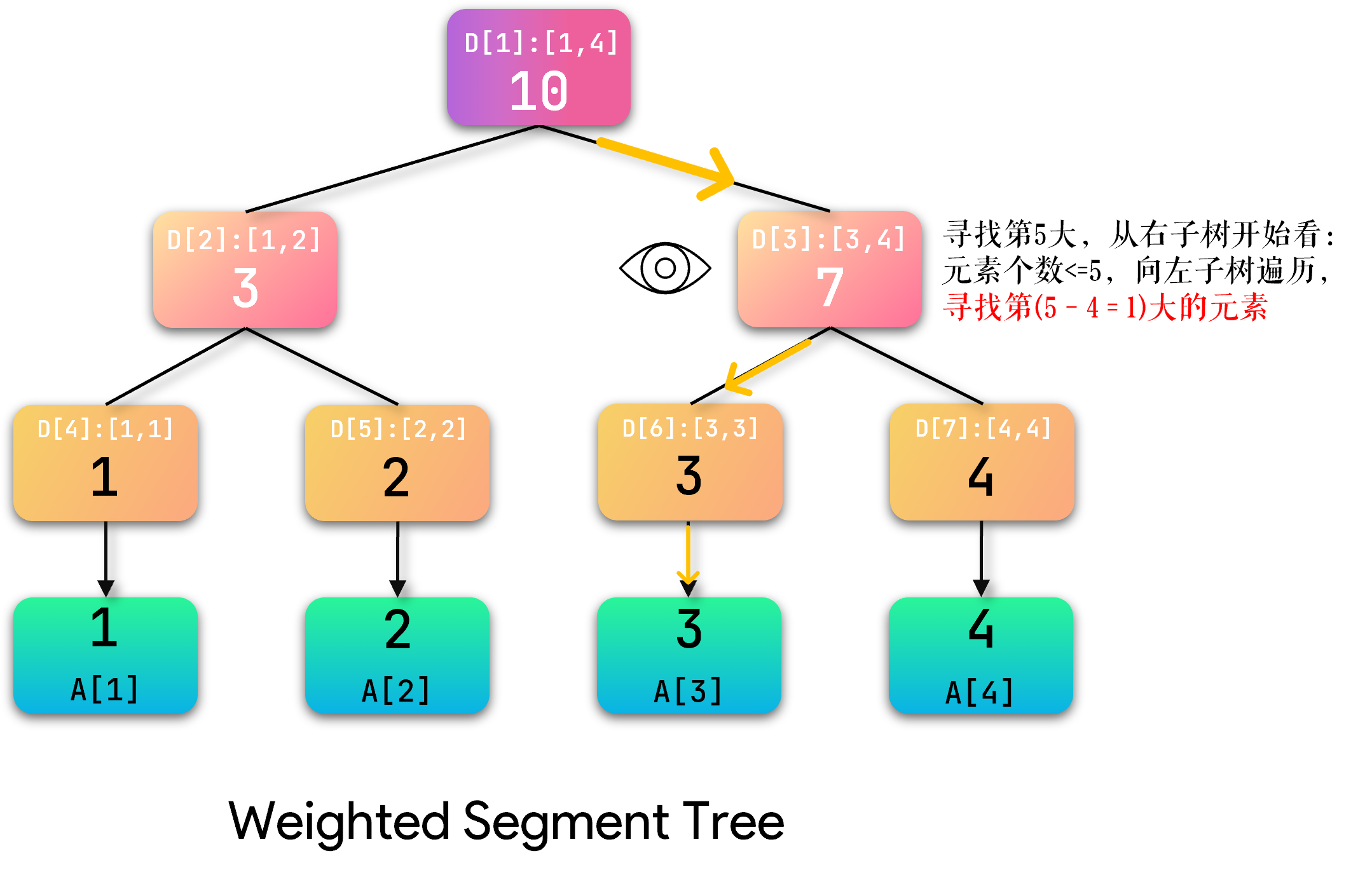
寻找第 K K K小的操作与上方类似，区别在于相对于起点OR终点而言(遍历时对左右子树的判断顺序)。

再次回顾整个步骤：对于整列数中第 K K K大/小的值，我们从根节点开始判断（这里按第 K K K大为例），如果 K K K比右儿子大，就说明第 K K K大的数在左子树中。然后， K K K要减去右子节点的值。（这是因为继续递归下去的时候，正确答案，整个区间的第 K K K大已经不再是左子树表示区间的第 K K K大了)。如此递归到叶子节点时即为答案

根据以上分析步骤，我们可以写出查询第 K K K大和第 K K K小的函数：

int query_kth(int pos, int l, int r, int k){
    if(l == r) return l;
    int mid = (l + r) >> 1, right = tree[pos