目录
一.基本概念
1.1 什么是计算?
关于有穷性
什么是好算法?
1.2 算法分析是干什么的?
T(n)
怎样评价算法优劣?
大O记号法 - 确定算法上界(最坏情况)
Ω表示法 - 确定算法下界(最好情况)
1.3 常见的复杂度
各种级别的复杂度 总结对比
二. 算法分析详解
2.1 算法分析的主要方法如下
2.2 基本的数学知识回顾
级数
循环 vs 级数
2.3 封底估计
三. 经典算法
3.1 迭代 vs 递归:减而知之
例子:数字求和
算法分析 - 递归跟踪:
算法分析 - 递推分析:
例子:数组倒置
3.2 迭代 vs 递归:分治法
例子:数组求和
例子:迭代找最大值和次大值
3.3 迭代 vs 递归:动态规划
斐波那契数列
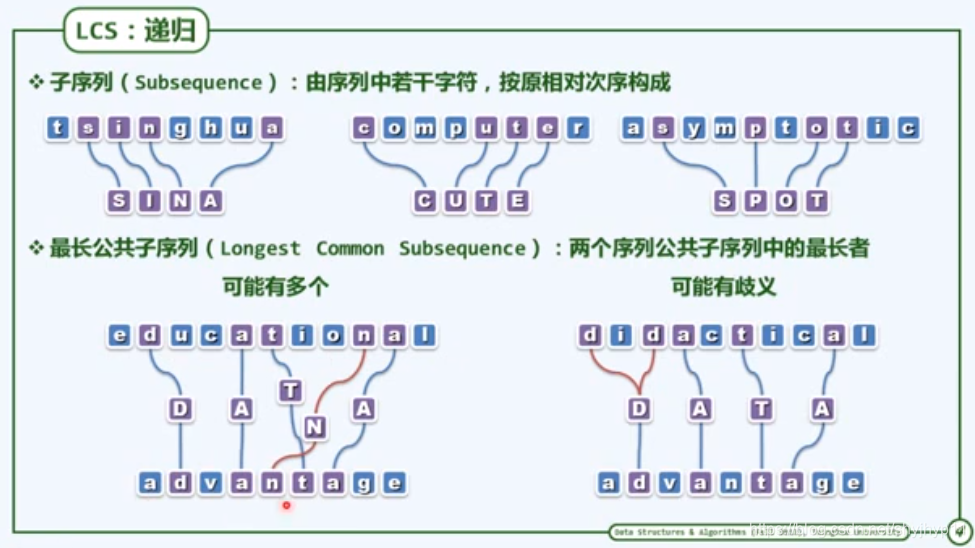
寻找两个字符串中的最长公共子序列(LCS)
TO-DO问题:渐进阶;递归;分治;排序;动态规划;贪心;图遍历; NP问题
一.基本概念 1.1 什么是计算?计算 = 信息处理 借助某种工具,遵照一定规则,以明确而机械的形式进行。

一个悬而未决的一个“算法”:希尔顿序列(Hailstone Sequence)
希尔顿序列问题是一个著名的数学问题,至今没有证明其正确性,也没证明其是错误的,即任何一个正整数N,如果是偶数的话就除以2,如果是奇数的话就乘以3再加上1,最后这个数都会变为1。由于不能证明这个程序的“有穷性”,故不能说该程序是一个算法。其表达式如下:

分析算法的 a.正确性 b.成本;一般关注的是成本中的时间成本。
同一个算法A,针对不同的问题实例P,表现是不一样的,为了度量算法的优劣,对问题实例P进行分类,分类的依据是问题实例的规模,进行等价类的划分。

用n来代表问题P的规模大小,T表示计算成本。
T(n)表示: 规模为n的问题实例P,在算法A的作用下的,计算成本。

针对同一问题P,使用不同算法A1,A2,A3...,如何评价优劣?

图灵机模型(Turing Machine)
针对上述问题(不同算法,可能更适应不同规模的输入....),评价算法优劣的解决方法:图灵机模型(Turing Machine)
参考:https://blog.csdn.net/weixin_30335353/article/details/97863943


RAM模型(Random Access Machine)
与此类似,还有RAM模型(Random Access Machine), 将算法的评价标准,进一步抽象,抽象为基本操作的次数(尺子)的评价。
此时,T(n) = 求解规模为n的问题时,所需要执行的基本操作次数。这样就摆脱了比如硬件、编程语言、代码质量等对算法评价的影响,成为一种理想的、有意义的、可信的研究模型。

用的最多的分析,度量悲观情况是什么样子。

大O记号法:T (n) = O( f(n) )
将T(n)表示为一个大O函数,函数的自变量为f(n),即完成了用 f(n)的形式表示T(n)。
O( f(n) ) 表示:存在一个大于0的常数c,当问题规模 n 远远大于2时,有 T(n) 小于 c倍的 f(n) 。
这样,使用 O( f(n) ) 简洁明了的反映出了 T(n) 的变化趋势, 同时反映出了问题规模的上界。

确切的解,用θ表示法

常数复杂度O(1)
对数复杂度(或者称 对数多项式复杂度) ![]()
多项式复杂度(可解的)![]()
指数复杂度(不可解的)![]()




指数复杂度不可解的一个例子:



在渐进意义上,c++等编程语言的基本指令,同常数条RAM的基本指令,基本相当,所以,通常会使用编程语言中,基本指令的条数来衡量算法复杂度。
2.1 算法分析的主要方法如下
包含算数级数,幂方级数,几何级数,收敛级数,调和级数,对数级数。



几何级数的时间复杂度,与它的末项同阶。

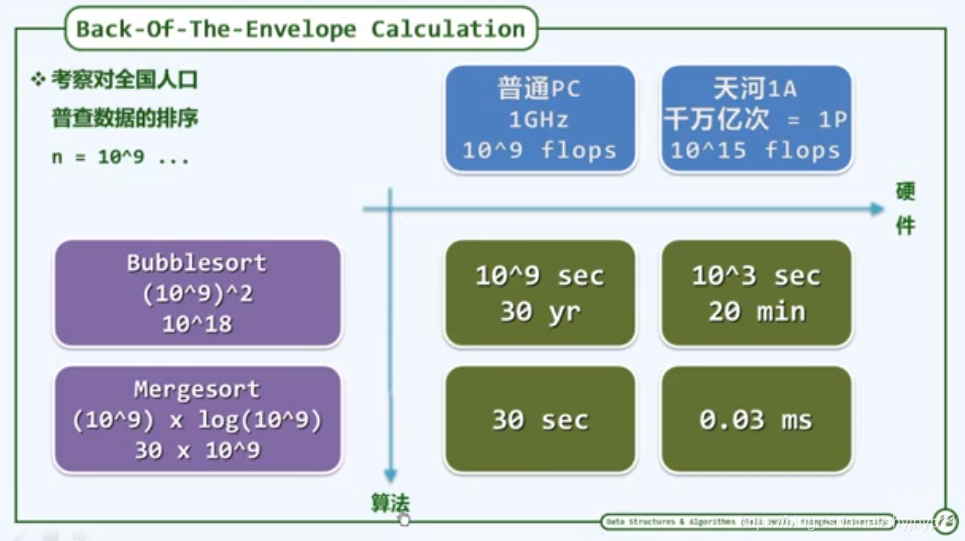
算法定量的估计,Back-of-The-Envelope Calculation
"三生三世"中的一天,正如一天中的一秒一样长。
熟知以下的时间概念:

通过提高硬件,可以将30 year 的计算时间缩短到 20 min;通过算法的改进,可以将 30 year 缩短到 30 seconds,课件算法改进的重要性。
三. 经典算法 3.1 迭代 vs 递归:减而知之 例子:数字求和

空间复杂度的考量:除了输入本身所占的空间之外,我们需要的,另加的,计算所必须的那些空间的总量。
减而知之(Decrease-and-conquer):不是平均分配问题,而是蚂蚁吞大象的方式。

分析时间复杂度时,递归的表达式可以直接抹掉(忽略掉)。
算法分析 - 递归跟踪:


分治(分而治之,Divide-and-conquer):分成的子问题,规模相当。


时间复杂度分析思想:
画出递归跟踪,可以看出,各层之间构成是几何级数关系;从渐进意义上来看,其时间复杂度等于最低层的实例的个数(sum(0,0) sum(1,1) ...),一共n个实例,所以可以直接看出,该算法的时间复杂度是O(n).

从递推的角度分析如下:列出递推方程,求解T(n).

方法一:两次扫描,第一次找最大值,第二次分成两块,找次大值

方法二:两个索引,一次扫描,找到最大值和次大值

方法三:递归 加 分治的方法,将数组拆分成两半,分别找各自一半中的最大值和次大值,然后比较两个分组中最大值和次大值
如: 左侧一半最大值次大值分别是 x1L, x2L, 右侧的最大值次大值分别是x1R,x2R; 先比两者的最大值,若右侧的最大值小于左侧的最大值,则得到整个数组的最大值,然后拿右侧的最大值和左侧的次大值比较,以此得出整个数组的次大值。

在找到问题的递归解法之后,将其等效的转换为迭代的形式。
基本思想:取决于该问题是否能用动态规划解决的是这些”小问题“会不会被被重复调用。(每个递归实例只需计算一次,将递归转成迭代的方法)
如何理解动态规划? https://www.zhihu.com/question/39948290
斐波那契数列
上述算法,计算第43项需要1s, 计算67项需要1day, 计算92项,则需要3个世纪...
采用如下递归跟踪的方法,可以看出存在大量重复计算的实例。
如右侧的一个例子,上台阶问题:从第0阶台阶,到第6阶台阶,有两种走法,每次走一个台阶,或者每次走两个台阶,一共有多少种走法,6个台阶走法数就是斐波那契数列的第6项。

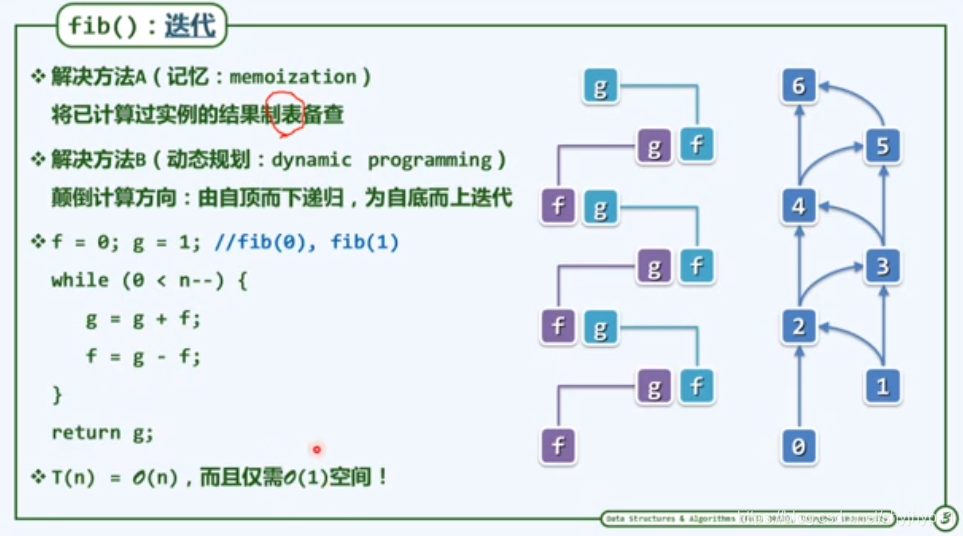
动态规定的思想(迭代的算法):
g f:通过迭代的方法,使得程序始终指向相邻的两阶,即相邻的两项,整体呈现出不断的交替的,滚动的方式不断向前推进,直到最终解。
参考视频如下:




分析可知,使用递归的复杂度O(2^n), 而递归过程中有太多的重复的实例的计算,所以应该考虑到使用迭代的方式,进行计算,基于迭代的动态规划算法的复杂度只有O(n*m),在递归中,每个实例只需计算一次,大大简化了计算量。

总结:
递归,虽然可以很容易帮助我们找到一个正确的解,但是如果要提高效率,使之变成一个实用算法的话,我们往往还需要进一步的调试,而在这个过程中,动态规划,扮演着重要的角色。
参考:邓俊辉 算法 清华 https://www.bilibili.com/video/av75509584?p=1



