数学_矩阵向量求导公式相关

目录

一. 向量变元的实值标量函数

 1、四个法则

 2、几个公式

二. 矩阵变元的实值标量函数 

1、四则运算 

2、几个公式 

求导公式

参考：矩阵分析与应用 张贤达 第五章 梯度分析和最优化 P271

一. 向量变元的实值标量函数

本节证明过程参考：矩阵求导公式的数学推导（矩阵求导——基础篇） - 知乎

设：

 1、四个法则

 

 

 

 2、几个公式

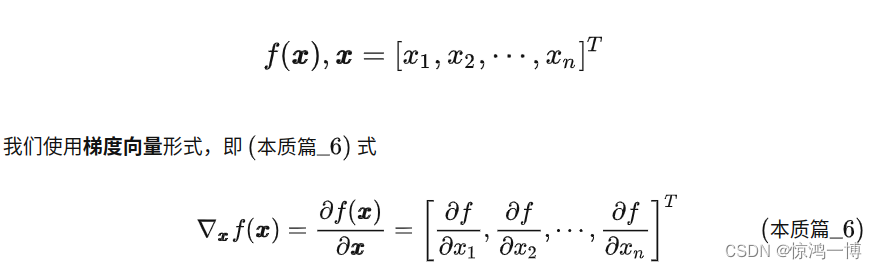
2.1 向量x与常数向量a的乘积，对该向量x求导

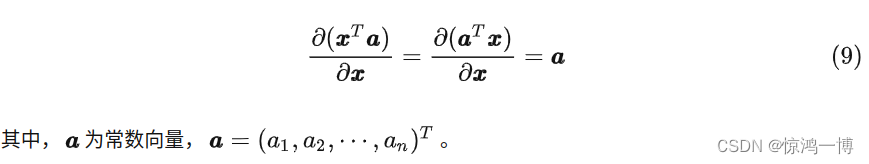
 2.2 向量x的转置与自身的乘积，对该向量x求导

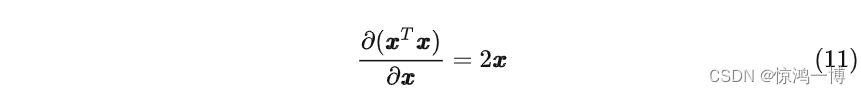
 2.3 向量x的转置乘以一个常数矩阵，再乘以该向量，对该向量求导

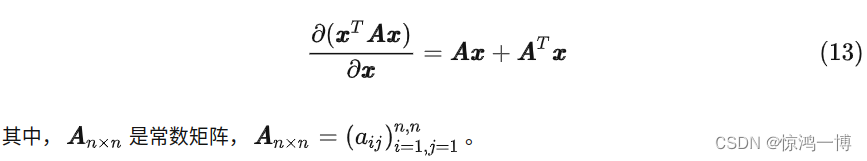
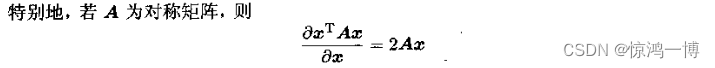 2.4 向量x与两个常数向量乘积的求导

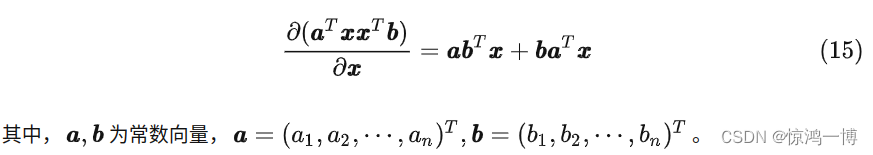
2.5 几个其它公式

2.5.1 向量x的转置对自身的导数，等于单位向量I

2.5.2  向量x的转置乘以矩阵A, 乘以向量y, 对向量x的导数

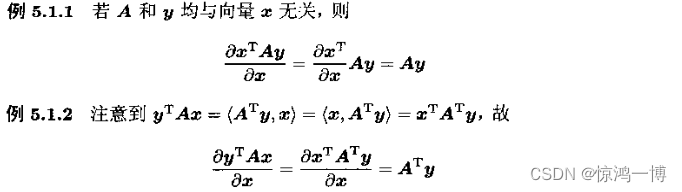
2.5.3 设A为m*n矩阵，x为n*1向量，向量(Ax)对x求导，等于矩阵A的转置

 

二. 矩阵变元的实值标量函数 

 设：

1、四则运算 

 

2、几个公式  

2.1 常数向量a的转置乘以矩阵X,再乘以常数向量b，对矩阵X的导数

（分子是一个标量，分母是一个矩阵）

2.1 常数向量a的转置乘以矩阵X的转置,再乘以常数向量b，对矩阵X的导数 

（分子是一个标量，分母是一个矩阵）

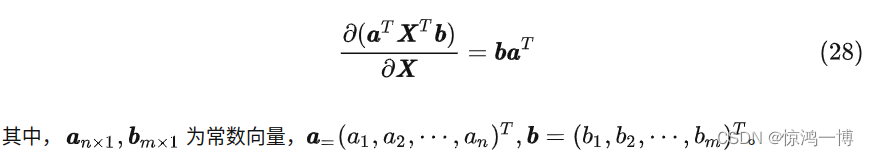
 2.3 常数向量a的转置乘以矩阵X，再乘以矩阵X的转置,再乘以常数向量b，对矩阵X的导数 

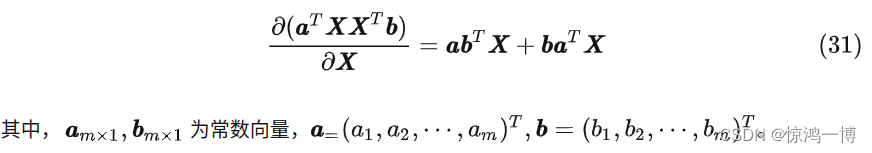
2.3 常数向量a的转置乘以矩阵X的转置，再乘以矩阵X,再乘以常数向量b，对矩阵X的导数  

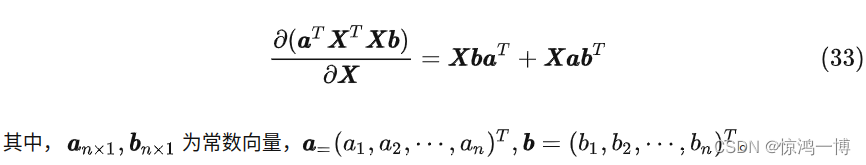
参考：矩阵求导公式的数学推导（矩阵求导——基础篇） - 知乎

张贤达《矩阵分析与应用（第二版）》P147