目录
论文基本情况
摘要
1 介绍
2 相关工作
3 方法
3.1 稀疏深度输入参数化
3.2 稀疏模式选择
4 试验设置
4.1 架构
4.2 数据库
4.3 大致的训练特征和性能评估
5 结果与分析
5.1 室内场景NYUv2
5.2 计算分析
5. 3 将D3推广为多种模式以及S2的影响
5.4 将D3模型推广到室外
5.5 鲁棒性测试(Robustness Tests)
5.6 讨论
6 总结
参考
论文基本情况- 题目: Estimating Depth from RGB and Sparse Sensing
- 作者：Zhao Chen, Vijay Badrinarayanan,Gilad Drozdov, and Andrew Rabinovich
- 单位：AR公司 Magic Leap, Sunnyvale CA 94089, USA
- 出处：ECCV 2018
- (启发点：下划线)
我们提出了一个深度模型，该模型可以根据已知深度非常稀疏的像素，和RGB图像准确生成密集的深度图。
该模型可同时用于室内/室外场景，
- 并在NYUv2和KITTI数据集上以接近实时的速度生成最新的密集深度图。
- 即使每10000个图像像素中只有1个深度值，我们也超越了单目深度估计的最新技术，并且在所有稀疏度级别上，我们都优于其他稀疏到密集的深度方法。
- 凭借1/256图像像素的深度值，我们在室内场景上实现的平均误差小于实际深度的1％，可与消费级深度传感器硬件的性能相媲美。
- 我们的实验表明，确实有可能有效地转换使用，例如，将低功率深度传感器或SLAM系统转换成高质量的密集深度图。
关键词：稀疏到稠密深度，深度估计，深度学习
一句话说明： 从groundtruth中采样出不同稀疏程度的稀疏图进行邻近填充，生成邻近填充图S1；定义一张Mask图(有深度的点值为1，没有深度的点值为0)，变换出一张欧几里得距离图S2, 将S1/S2/RBG三个输入，送到网络中，计算输出残差，将残差添加到稀疏输入图S1中以获得最终深度图估计；网络结构基于[2]中使用的网络，但使用DenseNet [9]块代替Inception [32]块。
1 介绍对于虚拟/混合现实，自动驾驶汽车和机器人等领域中的各种场景理解应用而言，高效，准确和实时的深度估计至关重要。当前，消费级的Kinect v2深度传感器消耗约15W的功率，仅在4.5m的有限范围内在室内工作，并在环境光线增加的情况下退化[8]。作为参考，未来的VR / MR头戴式深度摄像头将需要消耗1/100的功率，并且在RGB摄像头的完整FOV和分辨率下，其范围为1-80m（室内和室外）。这样的要求为联合开发节能的深度硬件和深度估计模型提供了机会。我们的工作开始从这个角度处理深度估计。
由于其固有的尺度模糊性，单目深度估计是一个具有挑战性的问题，最新的模型[4，17]在流行的大规模NYUv2室内数据集上仍然产生> 12％的平均绝对相对误差[24]。这样的误差对于诸如3D重建或跟踪之类的应用是禁止的，并且与诸如Kinect之类的深度传感器相距甚远，该传感器在室内的相对深度误差约为1％[14，25]。
认识到单眼深度估计的局限性，我们为深度模型提供了稀疏的测量深度以及RGB图像（见图1），以便估计完整的深度图。这种稀疏的深度解决了深度标度的歧义，并且可以从例如
- 飞行时间传感器[8]，
- 可信的立体匹配，
- 类似LiDAR的传感器
- 或定制设计的稀疏传感器中的照明稀疏图案中获取。
我们表明，尽管仅观察了深度图的一小部分，但所得模型仍可以提供与现代深度传感器相当的性能。我们相信我们的结果可以激励更小巧，更节能的深度传感器硬件的设计。由于现在的目标是致密化稀疏的深度图（带有来自RGB图像的其他提示），因此我们将模型称为“深度深度稠密化（Deep Depth Densification）”或D3。
我们的D3模型的一个优点是，它可以适应任意稀疏深度输入模式，每个模式都可以对应一个相关的物理系统。
- 规则的稀疏深度网格可能来自低功率深度传感器，
- 而某些兴趣点稀疏模式（例如ORB [27]或SIFT [21]）可以从现代SLAM系统[23]输出。
在这项工作的主体中，尽管我们在补充材料中详细介绍了ORB稀疏模式的实验，但由于它们易于解释且与现有深度传感器硬件具有直接相关性，因此我们将重点关注常规网格模式。
我们对深度估计领域的贡献如下：
- 1.一种用于密集场景深度估计的深度网络模型，其精确度可与常规深度传感器相比。
- 2.深度估计模型，可同时在室内和室外场景下使用，并且对常见的测量误差具有鲁棒性。
- 3.一种灵活，可逆的参数化稀疏深度输入的方法，可以在训练和测试期间适应任意稀疏输入模式。
在深度学习出现之前，深度估计已经在计算机视觉中得到了解决[28，29]。然而，产生全分辨率逐像素预测图的编码器-解码器深层网络体系结构[1，20]的普及，使深层神经网络特别适合此任务。无论是通过（典型方法）
- 将CRF（Conditional Random Field）与深网融合(deep nets)[37]；
- 利用几何形状和立体一致性[5，16]；
- 还是探索新颖的深层架构[17]，
这些进展都促使人们对深度估计的深层方法进行了大量研究。计算机视觉的深度通常用作执行其他感知任务的组件。（意义）
- 深度深度估计的第一种方法之一是同时估计多任务体系结构中的表面法线和分割[4]。
- 其他多任务视觉网络[3、12、34]也通常使用深度作为补充输出，以提高整体网络性能。
- 使用深度作为显式输入在计算机视觉中也很常见，在跟踪[30，33]，SLAM系统[13，36]和3d重建/检测[7，19]中有大量应用。
显然，对高质量深度图的需求迫在眉睫，但是当前的深度硬件解决方案非常耗电，具有严重的范围限制[8]，并且当前的传统深度估计方法[4、17]无法实现必要的精度取代此类硬件。（面临问题）
这些挑战自然会导致深度稠密化，这是将深度学习的力量与节能的稀疏深度传感器相结合的折中方法(a middle ground)。
- 深度稠密化与深度超分辨率有关[10，31]，
- 但是超分辨率通常使用双线性或双三次降采样深度图作为输入，因此仍然隐式包含来自低分辨率图中所有像素的信息。
- 真正的稀疏传感器将无法访问此附加信息，并且往往使估算问题变得更加容易（请参阅补充材料）。
- [22]和[23]中的工作遵循了更困难的致密化范式，其中仅提供了几个测量深度的像素。我们将证明我们的致密化网络优于[22]和[23]中的方法。
我们希望能够适应任意稀疏输入模式的稀疏深度输入的参数化。 这不仅应允许在不同的深度模型之间，甚至在训练和测试期间在同一模型内都可以改变这种模式。 因此，我们不建议将高度不连续的稀疏深度图直接馈入我们的深度深度致密化（D3）模型（如图1所示），而是建议对稀疏深度输入进行更灵活的参数化。
在每个训练步骤中，我们参数化的输入是：
- 1. I(x,y) 和D(x,y) ：RGB矢量值图像I和地面真实深度D。两个地图的尺寸均为H×W。 D中的无效值被编码为零。
- 2. M(x,y) ：尺寸为H×W的二进制图案掩模，其中M(x,y) = 1定义了我们所需深度样本的(x,y)位置。 对M(x,y) 进行预处理，以便M(x,y)= 1的所有点都必须对应于有效深度点（D(x,y)> 0）。 （请参阅算法1）。
从I，D和M，我们为稀疏深度输入形成两个映射图（map）：S1(x,y)和S2(x,y)。 两个映射图的尺寸均为H×W（示例请参见图2）。
- – S1(x,y) 是稀疏深度 M(x,y) * D(x,y) 的NN（最近邻居）填充。
- – S2(x,y) 是M(x,y)的欧几里得距离变换，即(x,y)与最近的点 (x', y') 之间的L2距离，其中M(x',y') = 1。
稀疏深度输入的最终参数化是 S1(x,y) 和 S2(x,y) 的串联，其总尺寸为H×W×2。 算法1中对此过程进行了描述。参数化速度很快，最多包含两个欧几里德变换。 所得的NN图S1在任何地方都不为零，这使我们可以将致密化问题视为相对于S1的残差预测。 距离图S2表示模型有关图案掩模 M(x,y) 的信息，并作为模型应输出的残差大小的先验值（即距离已知深度像素较远的点，往往会产生更高的残差）。 包含S2可以大大提高模型性能和训练稳定性，尤其是在训练过程中使用多个稀疏模式时（请参阅第5.3节）。
在这项工作中，我们主要关注规则的网格模式，因为它们是高覆盖率的稀疏映射，可以与以前的工作（通常假定为网格状的稀疏模式）进行直接比较（如[22]），但是我们的方法可以完全推广到其他模式 类似于ORB（请参阅补充材料）。
3.2 稀疏模式选择对于规则的网格图案，当选择图案蒙版M（x，y）时，我们试图通过在x和y方向上的后续模式点之间强制相等的间距，来确保最小的空间偏差。这导致了稀疏深度图S1？中正方形区域的棋盘格图案（见图2）。当一个深度模型必须容纳不同分辨率的图像时，这种策略很方便，因为我们可以简单地将M（x，y）中的正方形图案从一种分辨率扩展到另一种分辨率。为了便于解释，我们将始终使用接近整数下采样级别的稀疏模式；对于A×A的下采样系数，我们以
深度值 ？作为稀疏输入(take depth values as the sparse input)。例如，在480×640图像上进行24×24下采样，这将是总像素的0.18％。
根据经验，我们观察到在训练期间改变稀疏模式M（x，y）是有益的。对于N个稀疏点的理想最终模式，我们采用慢衰减学习方案，遵循
训练0≤t≤80000步。这样的方案开始于训练六次稀疏的模式密度，并随着训练的进行向最终密度平滑衰减。与静态稀疏模式相比，使用该衰减方案时，训练L2损失以及平均相对误差相对减少了约3％。我们还可以在每个训练步骤中以随机变化的采样密度进行训练。我们在5.3节中显示的结果是一个深度模型，该模型在不同的采样密度下可以同时很好地执行。
我们将网络架构（参见图3）基于[2]中使用的网络，但使用DenseNet [9]块代替Inception [32]块。我们凭经验发现，对于我们提出的模型而言，在整个深度网络中承载稀疏深度信息至关重要，而DenseNet的残差性质（residual）非常适合此要求。为了获得最佳结果，我们的架构保留了多种分辨率的特征图，以便在解码阶段将其重新添加到网络中。
除了第一个和最后一个块（它们是简单的3x3stride-2卷积层）之外，图3中的每个块都代表一个DenseNet模块（请参见图3插图，了解精确的模块示意图）。稀疏输入[S1，S2]的副本将作为每个模块的附加输入出现，将其降采样为适当的分辨率。每个DenseNet模块由2L层组成，每层k个特征图。我们使用L = 5和k =12。在下采样/上采样块中，最终卷积跨度为2。将网络的（残差）输出，添加到稀疏输入图S1中？以获得最终深度图估计。
Fig.3：D3网络架构。 我们提出的多尺度深度网络将以S1和S2串联的RGB图像作为输入。 第一个和最后一个计算块是简单的3x3 stride-2卷积，但其他所有块都是DenseNet模块[9]（请参见插图）。 网络中的所有卷积层都进行了归一化（batch normalized）[11]，并使用了ReLU。 网络输出一个残差，该残差被添加到稀疏深度图S1，以产生最终的密集深度预测。
4.2 数据库我们对室内和室外场景进行了广泛的实验。对于室内场景，我们使用NYUv2 [24]数据集，该数据集提供了使用Kinect V1传感器拍摄的高质量480×640深度数据，范围可达10m。缺少的深度值使用标准方法填充[18]。我们使用249/215训练/验证场景的官方划分，并从训练场景中采样了26331个图像。我们通过水平翻转进一步增强训练集。我们对654张图像的标准验证集进行测试，以与其他方法进行比较。
对于室外场景，我们使用KITTI道路场景数据集[35]，其深度范围可达〜85m。 KITTI提供了超过80000张图像进行训练，我们通过水平翻转进一步增强了图像。我们对完整的验证集（约10％的训练集）进行测试。 KITTI图像的分辨率为1392×512，但我们在训练过程中随机抽取了480×640的作物，以便使用NYUv2数据进行联合训练。 640个水平像素是随机采样的，而480个垂直像素是图像的480个底部像素（因为KITTI仅向地面提供LiDAR GT深度）。 KITTI中使用的LiDAR投影导致深度图非常稀疏（每个图像仅标注了约10％的深度），并且我们仅对具有GT深度的点评估模型。
4.3 大致的训练特征和性能评估在我们所有的实验中，我们使用Tensorflow 1.2.1在4个Maxwell Titan X GTX GPU上以 batch size 为8 的大小进行训练。 我们训练了80000 batches，并以1e-3的学习率开始，每25000步将学习率降低0.2。 我们使用Adam [15]作为我们的优化器，并使用标准的像素级L2损失进行训练。 使用标准指标[4，23]根据有效的GT深度值评估我们的深度估计模型。 设y为预测深度，y为数据集中N个像素的GT深度。 我们测量：
- （1）均方根误差（RMSE）：
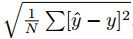， - （2）平均绝对相对误差（MRE）：
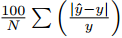，以及 - （3） Delta阈值（δi）：
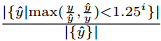。 δi是在由常数i控制的阈值下具有相对误差的像素百分比。
在这里，我们介绍室内（NYUv2）和室外（KITTI）数据集的D3模型的结果和分析。 我们进一步证明D3对输入错误具有鲁棒性，并且可以推广到多个稀疏输入模式。
5.1 室内场景NYUv2
从表1中可以看出，与[23]和[22] 2中的结果相比，D3网络在所有模式稀疏性方面都为所有指标1提供了卓越的性能。
...
5.2 计算分析我们在NYUv2数据集上的网络预测的可视化效果如图6所示。在高度稀疏的48×48下采样中，我们的D3网络已经显示出比没有任何稀疏输入的普通网络有了显着的改进。 我们在这里注意到，尽管网络输出作为残差添加到具有许多一阶不连续性的稀疏映射中，但最终预测看起来很平滑并且相对没有锋利的边缘伪像。 确实，在图6的最后一列中，我们可以看到我们的网络产生的直接残差预测还如何包含尖锐的特征，从而消除了稀疏映射中的非平滑性。
图6：NYUv2上D3预测的可视化。 左一列：RGB和GT深度示例。 中栏：针对稀疏性，顶部为稀疏S1映射，底部为D3网络预测。 Vanilla网络没有稀疏输入的情况（单眼深度估计）。 最后一栏：D3残差预测（与S1相加以获得最终预测）和最终估计值相对于GT的误差图。 距离越远，误差越大。 残差以灰色绘制，并以|δ|为上限 ≤1以获得更好的可视化； 它们表现出与S1类似的鲜明特征，展示了D3模型如何消除S1的不平滑度。
因此，对于全分辨率480×640输入，网络可以接近实时速度，并且我们期望通过深度网络的权重量化和其他优化方法可以进一步提高这些速度[6]。 更详细地讲，以一半的分辨率运行将导致我们更薄的D3网络以> 60fps的实时速度运行。 该速度对于深度作为主要组成部分的许多应用领域来说，至关重要。
5. 3 将D3推广为多种模式以及S2的影响
通过我们的实验，我们展示了D3模型在各种设置下，进行稀疏深度测量并将其转换为密集的深度图时的效果如何。 最值得注意的是，我们的模型在室内和室外场景下都能同时表现出色。 我们将模型的整体性能归因于许多因素。 从表2可以看出，我们的多尺度体系结构的设计对于优化性能很重要，在该体系中，稀疏输入以各种尺度摄取，输出被视为S1的残差。 如图7所示，我们提出的稀疏输入参数化显然可以实现更好和更稳定的训练。最后，训练课程的设计（在训练期间我们在深度输入中使用不同的稀疏度）也起着重要的作用。 这样的策略使模型能够健壮地测试稀疏性的时间变化（请参见图7）并减少总体误差。
6 总结我们已经证明，训练有序的深度深度致密化（D3）网络，可以使用稀疏的深度信息和已注册的RGB图像来生成高质量的密集深度图。我们对稀疏深度信息的灵活参数化，使模型可以轻松推广到多种场景类型（在1m到80m深度的室内和室外图像上同时工作）以及各种稀疏输入模式。即使在室内场景具有相当强烈的稀疏性（fairly aggressive sparsities），我们也可以将平均绝对相对误差控制在1％以下，与消费级深度传感器硬件的性能相当。我们还发现，我们的模型对于各种输入错误均相当健壮。
因此，我们表明，对于室内或室外需要RGBD输入的应用，稀疏深度测量就足够了。我们研究的下一步自然是要评估密集的深度图在3d重建算法，跟踪系统或相关视觉任务（例如表面法线预测）的感知模型中的表现。我们希望我们的工作能够从软件和硬件的角度激发对稀疏深度用途的更多研究。
参考- 2. Chen, W., Fu, Z., Yang, D., Deng, J.: Single-image depth perception in the wild. In: Advances in Neural Information Processing Systems. pp. 730–738 (2016)
- 4. Eigen, D., Fergus, R.: Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In: Proceedings of the IEEE International Conference on Computer Vision. pp. 2650–2658 (2015)
- 5. Garg, R., BG, V.K., Carneiro, G., Reid, I.: Unsupervised cnn for single view depth estimation: Geometry to the rescue. In: European Conference on Computer Vision. pp. 740–756. Springer (2016)
- 9. Huang, G., Liu, Z., Weinberger, K.Q., van der Maaten, L.: Densely connected convolutional networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition. vol. 1, p. 3 (2017)
- 16. Kuznietsov, Y., St¨uckler, J., Leibe, B.: Semi-supervised deep learning for monocular depth map prediction. In: Proc. of the IEEE Conference on Computer Vision and Pattern Recognition. pp. 6647–6655 (2017)
- 17. Laina, I., Rupprecht, C., Belagiannis, V., Tombari, F., Navab, N.: Deeper depth prediction with fully convolutional residual networks. In: 3D Vision (3DV), 2016 Fourth International Conference on. pp. 239–248. IEEE (2016)
- 20. Long, J., Shelhamer, E., Darrell, T.: Fully convolutional networks for semantic segmentation. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 3431–3440 (2015)
- 22. Lu, J., Forsyth, D.A., et al.: Sparse depth super resolution. In: CVPR. vol. 6 (2015)
- 23. Ma, F., Karaman, S.: Sparse-to-dense: Depth prediction from sparse depth samples and a single image. arXiv preprint arXiv:1709.07492 (2017) 后来接收：2018-ICRA
- 32. Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V., Rabinovich, A., et al.: Going deeper with convolutions. Cvpr (2015)
