目录
1. 图相关(Graph)
例1. 无向图的克隆
例2. 无向图中求最短路径的值
例3. 单词接龙
a. 从beginWord到endWord的最短转换序列中的单词数目(ladderLength)
b. 从beginWord到endWord的所有最短转换序列(findLadders)
例4. 有向图的拓扑排序 (Topological Sorting)
2. 搜索相关
例5. 组合(subsets)相关题目
a. 不含重复整数的集合的子集(leetcode78. 子集)
b. 含重复整数的数组的子集 (leetcode 90.子集 II)
c. 将一个 string 分割成回文子串 的所有方案
d. 组合总和(数组无重复元素,元素可使用多次,candidates ==> target)
e. 组合总和II(数组有重复元素,元素只可使用一次,candidates ==> target)
例6. 全排列(permutation)
a. 不含重复数字的数组的全排列
b. 含重复数字的数组的全排列
例7. N 皇后
a. 返回N皇后所有的解决方案
b. 返回N皇后所有的解决方案的个数
1. 图相关(Graph) 例1. 无向图的克隆描述:克隆一张无向图. 无向图的每个节点包含一个 label 和一个列表 neighbors. 保证每个节点的 label 互不相同.你的程序需要返回一个经过深度拷贝的新图. 新图和原图具有同样的结构,并且对新图的任何改动不会对原图造成任何影响.你需要返回与给定节点具有相同 label 的那个节点.关于无向图的表示: http://www.lintcode.com/help/graph/ (来源:lintcode 137 · 克隆图 = leetcode 133. 克隆图)
示例: 输入:adjList = [[2,4],[1,3],[2,4],[1,3]] 输出:[[2,4],[1,3],[2,4],[1,3]]
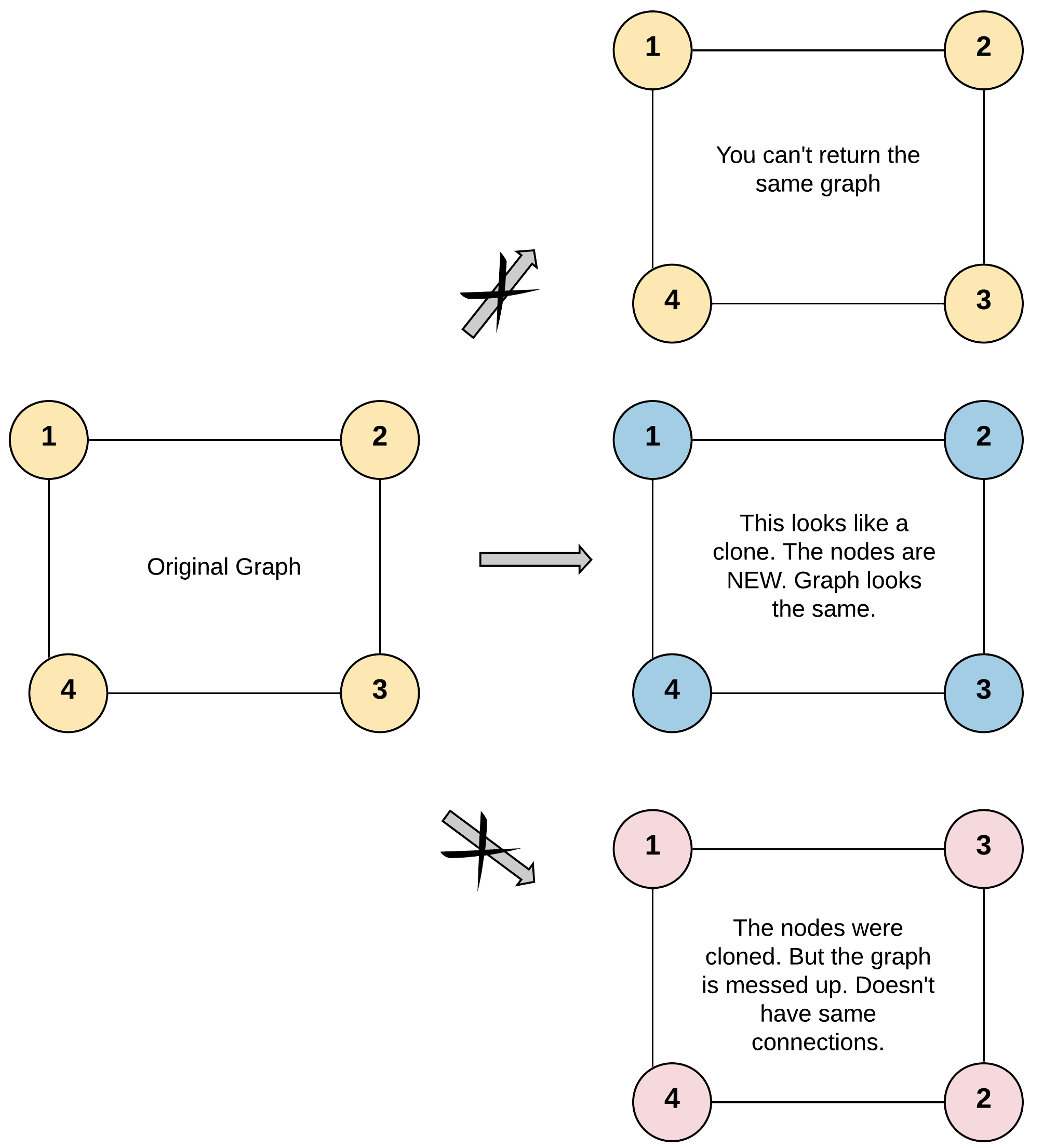
解释:图中有 4 个节点。 节点 1 的值是 1,它有两个邻居:节点 2 和 4 。 节点 2 的值是 2,它有两个邻居:节点 1 和 3 。 节点 3 的值是 3,它有两个邻居:节点 2 和 4 。 节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
代码
本题看似考察的是图,实际考察的是 广度优先遍历(BFS)。算法的整体框架也是BFS的模板(参考:二叉树遍历-例9)。 本文中采用一个队列(queue)来控制遍历的顺序; 采用一个哈希映射 (unorderd_map hashMap) 来保存新的图节点 和 复制 的节点 之间的对应关系,同时保证不遍历重复的元素。通过复制当前节点的所有邻近节点,将新的节点链接到新的邻居节点上,并依次加入hashMap中(为通过旧的节点找新的copy的节点作准备),同时依次加入到队列 queue 中(为对图中的每一个节点进行遍历作准备)。注意:这里定义了2个“跑腿的”指针 ( UndirectedGraphNode * oldNode; UndirectedGraphNode * newNode),使程序更直观可读。
/**
* Definition for undirected graph.
* struct UndirectedGraphNode {
* int label;
* vector neighbors;
* UndirectedGraphNode(int x) : label(x) {};
* };
*/
class Solution {
public:
UndirectedGraphNode* cloneGraph(UndirectedGraphNode* node) {
if (node == nullptr) {
return nullptr;
}
unordered_map hashMap;
queue que;
UndirectedGraphNode * oldNode = node; //特别注意: 这样定义使用很方便。
UndirectedGraphNode * newNode = new UndirectedGraphNode(oldNode->label);
hashMap[oldNode] = newNode;
que.push(oldNode);
while (!que.empty()) {
oldNode = que.front();
newNode = hashMap[oldNode];
que.pop();
for (int i = 0; i < oldNode->neighbors.size(); i++) {
UndirectedGraphNode * oldNeighbor = oldNode->neighbors[i];
if (hashMap.find(oldNeighbor) == hashMap.end()) {
UndirectedGraphNode * newNeighbor = new UndirectedGraphNode(oldNeighbor->label);
newNode->neighbors.push_back(newNeighbor); // 新的图上,进行边的链接
hashMap[oldNeighbor] = newNeighbor; // 保存新旧节点之间的映射关系
que.push(oldNeighbor);
} else {
newNode->neighbors.push_back(hashMap[oldNeighbor]); // 新的图上,进行边的链接
}
}
}
return hashMap[node]; // 注意返回值中的索引
}
};描述:给定一个无向图, 图中所有边的长度为1, 再选定图中的两个节点, 返回这两个节点之间最短的路径的长度。(来源:lintcode 814 · 无向图中的最短路径 中等)
样例 1: 输入: graph = {1,2,4#2,1,4#3,5#4,1,2#5,3}, node1 = 3, node2 = 5 输出: 1 解释: 1------2 3 \ | | \ | | \ | | 4 5样例 2: 输入: graph = {1,2,3,4#2,1,3#3,1#4,1,5#5,4}, node1 = 1, node2 = 5 输出: 2
代码
同样使用 宽度优先遍历BFS的模板, 这里定义一个 哈希映射(unordered_map hashMap;),记录每一个节点的最短路径值(距离起点的最短距离),从起始节点开始,遍历它的邻居节点,依次更新邻居节点的最短路径值。遍历当前节点的每一个邻居,若已经遍历过了,就不必更新它的最短路径值,否则等于当前节点的最短路径 + 1。中间过程中若遍历到的邻居节点就是目标节点,就直接返回 当前节点的最短路径值 + 1。
class Solution {
public:
/**
* @param graph: a list of Undirected graph node
* @param A: nodeA
* @param B: nodeB
* @return: the length of the shortest path
*/
int shortestPath(vector graph, UndirectedGraphNode* A, UndirectedGraphNode* B) {
if (graph.size() neighbors) { //遍历当前节点的每一个邻居,若已经遍历过了,就不必更新它的最短路径值,否则等于当前节点的最短路径 + 1
if (neighbor == B) {
return hashMap[curNode] + 1;
}
if (hashMap.find(neighbor) == hashMap.end()) {
hashMap[neighbor] = hashMap[curNode] + 1;
que.push(neighbor);
} else {
continue;
}
}
}
return -1;
}
};描述:字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:序列中第一个单词是 beginWord 。序列中最后一个单词是 endWord 。每次转换只能改变一个字母。转换过程中的中间单词必须是字典 wordList 中的单词。给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。(来源:leetcode 127. 单词接龙 ≈ lintcode 120 · 单词接龙 )示例 1: 输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"] 输出:5 解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。 示例 2: 输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"] 输出:0 解释:endWord "cog" 不在字典中,所以无法进行转换。提示:1 "log" -> "cog"
示例 2: 输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"] 输出:[ ] 解释:endWord "cog" 不在字典 wordList 中,所以不存在符合要求的转换序列。
代码 (BFS + DFS)

为了得到最短路径中的所有单词,我们这里需要定义两个map, 一个用于存储与当前单词连接(只相差一个字母)的所有单词 map neighborWords; 一个用于存储所有单词距离beginWord的距离 map distances; 我们在BFS过程中,对上述两个map进行统计, 在DFS中,从 beginWord 到 endWord 按层遍历,收集最短路径即可。
- 时间复杂度
O((V+E))- bfs:
O(V+E)遍历所有边E(即当前字符串的下一跳)和点V, - dfs:
O(size(dict))跑最后的最短路
- bfs:
- 空间复杂度
O(size(dict))- 存每个字符串与下一跳字符串的集合以及最短路径
class Solution {
private:
map distances; // 存入各个单词到 beginWord 的距离
map neighborWords; // 存入各个单词与之只相差一个字母的单词(即无向图中相连接的节点)
public:
vector findLadders(string beginWord, string endWord, vector& wordList) {
vector results; // 存放最终所有的最短转换序列
vector result; // 存放单条最短转换序列
result.push_back(beginWord); // 题目要求,若最短转换路径存在,则结果中应含有beginWord,不论字典中是否有该单词
unordered_set dict(wordList.begin(), wordList.end()); //单词放入hash set中方便O(1)级别的查找
// dict.insert(endWord); //lintcode上不要求end word 在词典中,需要加这行。leetcode不需要加此行
bfs(beginWord, endWord, dict); //广度优先遍历:统计各单词到beginWord的最短距离 以及 各单词的相邻单词
dfs(beginWord, endWord, dict, results, result); //从头到位遍历一遍,按“层” 存储最短路径
return results;
}
void bfs(string beginWord, string endWord, unordered_set& dict) {
queue que;
que.push(beginWord);
int length = beginWord.length();
int dis = 0;
distances[beginWord] = dis; //初始化
bool bFind = false;
while (!que.empty()) {
dis++; // 特别注意:距离在此加!每进入一层就加1
int size = que.size();
for (int i = 0; i < size; i++) {
string curWord = que.front();
que.pop();
for (string& newWord : getNeighbors(curWord, dict)) {
neighborWords[curWord].push_back(newWord); // 找到当前单词的邻居们,放入map
if (newWord == endWord) {
bFind = true;
}
if (distances.find(newWord) == distances.end()) { //newWord未添加到距离表(节点层号表)中时,防止第二次找到(如反向找到时)时更新原始的最短长度; 防止同一个单词添加到队列中多次。
distances[newWord] = dis;
que.push(newWord);
}
}
}
if (bFind == true) { //在遍历完当前层时,若找到了endWord就不再往下一层再遍历了。特别注意:在while大循环内!
break;
}
}
}
void dfs(string beginWord, string endWord, unordered_set& dict,
vector& results, vector result) {
if (beginWord == endWord) {
results.push_back(result);
}
vector neighbors = neighborWords[beginWord];
for (string& neighbor : neighbors) {
if (distances[neighbor] != distances[beginWord] + 1) { // 只遍历下一层的节点
continue;
}
result.push_back(neighbor);
dfs(neighbor, endWord, dict, results, result); // 递归时,从下一节点开始继续遍历
result.pop_back(); // 因为可能有另一条路径,所以要回溯当前节点,看旁支是否可以走
}
}
vector getNeighbors(string curWord, unordered_set& dict) { // 返回的neighbors包含了当前单词连接的所有节点(有前面的也有后面的)
vector res;
for (int i = 0; i < curWord.length(); i++) {
string newWord = curWord;
for (char newChar = 'a'; newChar B , 在拓扑排序中A一定在B之前. 拓扑排序中的第一个节点可以是图中的任何一个没有其他节点指向它的节点.
针对给定的有向图找到任意一种拓扑排序的顺序.你可以假设图中至少存在一种拓扑排序. 图结点的个数 B,被指向的节点B一定在A节点之后。有种分层排序的意味。所以,首先我们先要统计每一个节点的入度(被指向的次数)。然后对于入度为0的节点必定在第一梯队先被输出,然后采用宽度优先遍历(BFS)的模板,依次遍历每一个节点,每遍历到一次,入度对应的值减1,减到0时,就可以输出了。所以,我们可以采用哈希映射 (unordered_map hashMap;)来存储节点的入度,用 队列 (queue que; )来作BFS.
/**
* Definition for Directed graph.
* struct DirectedGraphNode {
* int label;
* vector neighbors;
* DirectedGraphNode(int x) : label(x) {};
* };
*/
class Solution {
public:
vector topSort(vector graph) {
vector result;
if (graph.size() == 0) { // 可以省略
return result;
}
unordered_map hashMap; // 统计各个图节点的入度 //入度为0的节点自然为拓扑排序的第一梯队
queue que; // 使用广度优先遍历 按"层"遍历图中的每一个节点
for (auto& node : graph) { // 注意:这里求的是节点的入度,对每一个节点求它的邻居(被指向/入度)出现的次数。而不是简单的统计graph中每个节点出现的次数。
for (auto& neighbor : node->neighbors ) {
if (hashMap.find(neighbor) == hashMap.end()) {
hashMap[neighbor] = 1;
} else {
hashMap[neighbor] += 1;
}
}
}
for (int i = 0; i < graph.size(); i++) { // 找到入度为0的节点,放入队列进行遍历,同时放入结果数组中
if (hashMap.find(graph[i]) == hashMap.end()) {
result.push_back(graph[i]);
que.push(graph[i]);
}
}
while (!que.empty()) {
DirectedGraphNode* curNode = que.front();
que.pop();
for (auto& neighbor : curNode->neighbors) {
hashMap[neighbor]--;
if (hashMap[neighbor] == 0) {
result.push_back(neighbor);
que.push(neighbor);
}
}
}
return result;
}
};
2. 搜索相关
例5. 组合(subsets)相关题目
求子集,递归中,遍历开始的位置:for (int i=pos; i 相当于放入[1,]
subSetsCore(nums, results, result, i + 1); //注意 i+1 // => 相当于放入[1,2],[1,3]
result.pop_back(); // => 回溯,从树根向上遍历删除
}
}
};
描述:给定一个可能具有重复数字的列表,返回其所有可能的子集。示例:输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
代码
特别注意:去重(树状结构的横向去重--for循环方向,去重重复的子集,如[1,2'] 和 [1,2'']中留第一个)的判断条件是
- if ( i != pos && nums[i] == nums[i-1] ) continue;
class Solution{
public:
vector subsetsWithDup(vector &nums){
vector results;
vector result;
sort(nums.begin(), nums.end()); //注意: 这里需要sort
subsetsWithDupCore(nums, results, result, 0);
return results;
}
void subsetsWithDupCore(const vector &nums, vector &results, //注意results和result是引用传递
vector &result, int pos){
results.push_back(result); //注意:这里空的也算子集的一部分
for (int i = pos; i < nums.size(); ++i){ //特别注意: 搜索开始的位置 i=pos
if (i != pos && nums[i] == nums[i-1]){ //特殊处理部分: 跳过重复的数字,不添加到候选子集中
continue;
}
result.push_back(nums[i]); // => 相当于放入[1,]
subsetsWithDupCore(nums, results, result, i + 1); //注意 i+1 // => 相当于放入[1,2],[1,3]
result.pop_back(); // => 回溯,从树根向上遍历删除
}
}
};描述:给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。回文串 是正着读和反着读都一样的字符串。(来源:lintcode 136 · 分割回文串 = leetcode 131. 分割回文串 = 算法笔记_面试题_15.回溯算法模板及示例 例2.1)示例 1: 输入:s = "aab" 输出:[["a","a","b"],["aa","b"]]示例 2: 输入:s = "a" 输出:[["a"]]
代码
本题 约等于 例a (不含重复整数的集合的子集), 依然是 一个 subsets的问题。将分割线作为子集中需要选择的数字,然后就等价于从 这些数字中依次选择子集,看每个子串片段是否为回文,直到分割到原始字符串结尾。树状图如下所示。代码大同小异。需要注意的是:每次判断的子串是 s.substr(pos, i - pos + 1); 其中 i 控制遍历字符串的层数, pos 控制子串开始的位置。递归时,使用 backTracking(s, results, result, i + 1);

class Solution {
public:
vector partition(string s) {
vector results;
if (s.empty()) {
return results;
}
vector result;
backTracking(s, results, result, 0);
return results;
}
void backTracking (string s, vector& results, vector result, int pos) {
if (pos == s.size()) {
results.push_back(result);
return; // 最好别少!!!
}
for (int i = pos; i < s.size(); i++) {
string subStr = s.substr(pos, i - pos + 1); // 从 pos 开始 ,长度为 i-pos+1 的子串
if (!isPalindrome(subStr)) {
continue; //表示以当前substr为根向下的分割方法(自上而下这条分支-纵向)都不符合条件。但不能时 return(相当于过滤到了下一条分支-横向,例子 ab不是 aba是的)
}
result.push_back(subStr);
backTracking(s, results, result, i + 1);
result.pop_back();
}
}
bool isPalindrome(string s) {
int start = 0;
int end = s.size() - 1;
for (; start < end; start++, end--) {
if (s[start] != s[end]) {
return false;
}
}
return true;
}
};数组无重复元素,元素可使用多次,candidates ==> target)
描述:给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。 对于给定的输入,保证和为 target 的不同组合数少于 150 个。(来源:leetcode 39. 组合总和 = lintcode 135 · 数字组合 = 算法笔记_面试题_15.回溯算法模板及示例 例1.3)示例 1: 输入:candidates = [2,3,6,7], target = 7 输出:[[2,2,3],[7]] 解释:2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选, 7 = 7 。 仅有这两种组合。示例 2: 输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]]
代码
仍然是subsets的模板,需要注意的是,数组中的数字可以重复选择,所以递归时 pos位置的参数是 i , 而不再是 i+1 (对于 for (int i = pos; i < candidates.size(); i++) )。同时,递归的退出条件也很巧妙,将 target 每次都减去 一个 可能的 candidate, 指导target == 0 时,则说明找到了目标数组
- backTracking( candidates, target - candidates[i], results, result, i );
另外,为了加速(进行剪枝),先进行排序,若当前的候选值 candidate 已经大于 目前剩余的 target值, 则经过排序后的后面的candidate可能更大于剩余的目标值,此时就可以直接return, 因为这条分支上不可能有答案了。
class Solution {
public:
vector combinationSum(vector& candidates, int target) {
vector results;
if (candidates.size() == 0) {
return results;
}
sort(candidates.begin(), candidates.end());// 为了剪枝加速,先要进行排序
vector result;
backTracking(candidates, target, results, result, 0);
return results;
}
void backTracking(vector& candidates, int target,
vector& results, vector result, int pos) {
if (target == 0) {
results.push_back(result);
}
//if (target < 0) {
// return;
//}
for (int i = pos; i < candidates.size(); i++) { // for循环每次从pos开始,而不是0开始,因为着组合中不能再倒着选回去(会造成结果重复)!
if (target < candidates[i]) { // 剪枝 加速方法
return;
}
result.push_back(candidates[i]);
backTracking(candidates, target - candidates[i], results, result, i); //特别注意:关键语句! 减号-使递归逐渐接近目标, i 表示可以重复选择
result.pop_back();
}
}
};数组有重复元素,元素只可使用一次,candidates ==> target)
描述:给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。(来源:leetcode 40. 组合总和 II = lintcode 153 · 数字组合 II 中等) 注意:解集不能包含重复的组合。 示例 1: 输入: candidates = [10,1,2,7,6,1,5], target = 8, 输出:[[1,1,6],[1,2,5],[1,7],[2,6]]示例 2: 输入: candidates = [2,5,2,1,2], target = 5, 输出:[[1,2,2],[5]]
代码
同样是subset的模板。需要注意的是:1). 因为数组中有重复元素,所以要先排序,在回溯函数中(对应树状结构上的)要横向去重:if (i != pos && candidates[i] == candidates[i-1]) continue; 2). 不可重复使用数组元素:所以递归时 i 要 变成 i + 1。
class Solution {
public:
vector combinationSum2(vector& candidates, int target) {
vector results;
int n = candidates.size();
if (n == 0) {
return results;
}
sort(candidates.begin(), candidates.end()); //特别注意:因为有重复,要先排序
vector result;
backTracking(candidates, results, result, target, 0);
return results;
}
void backTracking(vector& candidates, vector& results, vector result, int target, int pos) {
if (target == 0) { //终止条件
results.push_back(result);
return;
}
// if (target < 0 || pos == candidates.size()) { //可以省略,for中 if (num[i] > target)保证递归过来的taget>0; for中i target) { //剪枝加速
continue;
}
if (i != pos && candidates[i] == candidates[i-1]) { //特别注意:去除横向的重复子集如[1',7] 和 [1'',7]留下一个
continue;
}
result.push_back(candidates[i]);
backTracking(candidates, results, result, target - candidates[i], i + 1); //不可重复使用数组元素:所以递归时 i要 变成 i + 1
result.pop_back();
}
}
};下面的求全排列 ,递归中,遍历开始的位置:for (int i = 0; i < nums.size(); i++)
a. 不含重复数字的数组的全排列描述:给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。(leetcode 46. 全排列 = lintcode 15 · 全排列)示例 1: 输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示例 2: 输入:nums = [0,1] 输出:[[0,1],[1,0]]
代码
本文采用组合(subsets)方法的模板,采用回溯法 + visited数组去重。当然其他文章中采用的swap交换的方法也是极好的。
相比于 subsets,因为一个数可以使用多次,所以,递归中for循环 i 从 0 开始,而 i 每次也不必后移一位, 递归的句子不变。这里的for循环 从 0 开始的,所以每一轮递归中要考虑去除自己(比如 以2 开始的子集, 因为for循环从0开始,nums[0]=1 nums[1] = 2,此时就存在重复,使用visited数组跳过自己)。注意写法:if (visited[i] == true) continue;
class Solution {
public:
vector permute(vector& nums) {
vector results;
int n = nums.size();
if (n == 0) {
return results;
}
vector result;
vector visited(n, false); // 去重,记录是否已经访问过了
permuteCore(nums, results, result, visited);
return results;
}
void permuteCore(vector& nums, vector& results, vector result, vector& visited) {
if (result.size() == nums.size()) {
results.push_back(result);
}
for (int i = 0; i < nums.size(); i++) {
if (visited[i] == true) { // 去重,已经访问过的就跳过
continue;
}
result.push_back(nums[i]);
visited[i] = true; // visited数组 也一起 backtracking
permuteCore(nums, results, result, visited);
result.pop_back();
visited[i] = false;
}
}
};描述:给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。(来源:leetcode 47. 全排列 II)示例:输入:nums = [1,1,2] 输出:[[1,1,2], [1,2,1], [2,1,1]]
代码
因为有重复元素,就需要去重重复元素,在去重前,一定记得先排序!然后,判断前一个节点是否使用过进行去重。特别注意去重的判断条件:
if (visited[i] == true || (i != 0 && nums[i] == nums[i-1] && visited[i-1] == false)) continue;
(注意:nums[i] == nums[i-1] 对应的是 树状结构的横向去重--for循环方向(如[1', 1'', 2] 和 [1'', 1', 2]中留一个),同含重复数字的组合问题)
第一个判断条件:跳过自身(因为for循环每次都是从0开始的),跟不含重复数字的全排列一样。
第二个判断条件:对重复的元素进行跳过操作。特别注意:上面这行的跳过条件! false、true其实都可以。
- visited[i-1] == true: 说明同⼀树枝nums[i - 1]使⽤过, 对树枝进行剪枝;
- visited[i-1] == false:说明同一树层(效率更高)nums[i - 1]使⽤过(前一个节点已经搜索并回溯过了)。
请参考代码随想录的解释。

class Solution {
public:
vector permuteUnique(vector& nums) {
vector results;
int n = nums.size();
if (n == 0) {
return results;
}
sort(nums.begin(), nums.end()); //特别注意: 先排序!先排序,先排序!
vector result;
vector visited(n, false);
permuteUniqueCore(nums, results, result, visited);
return results;
}
void permuteUniqueCore(vector& nums, vector& results, vector result, vector& visited){
if (result.size() == nums.size()) {
results.push_back(result);
}
for (int i = 0; i < nums.size(); i++) {
if (visited[i] == true || (i != 0 && nums[i] == nums[i-1] && visited[i-1] == false)) {
continue; //注意:上面这行的跳过条件! false true都可以。// true:说明同⼀树枝nums[i - 1]使⽤过,对树枝进行剪枝 false:说明同一树层nums[i - 1]使⽤过(前一个节点已经搜索并回溯过了)
}
result.push_back(nums[i]);
visited[i] = true;
permuteUniqueCore(nums, results, result, visited);
result.pop_back();
visited[i] = false;
}
}
};描述:n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。(来源:leetcode 51. N 皇后 困难= lintcode 33 · N皇后问题(一)中等)示例 1:
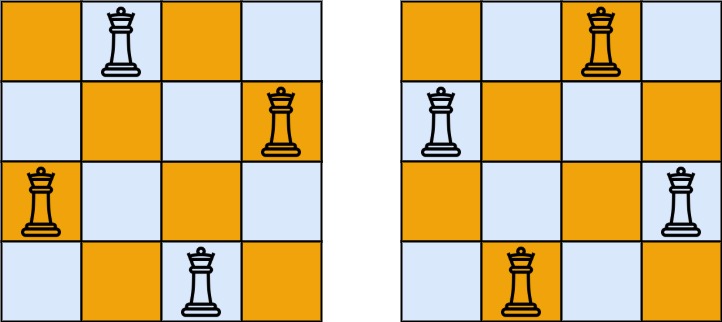
输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。示例 2: 输入:n = 1 输出:[["Q"]]
本题是一道搜索题目,使用朴素的暴力搜索方法,进行依次回溯式的搜索。需要注意的是,我们采用一个数组 vector cols 来保存一组可能的解决方案。
- cols中元素的索引:存放的是对应的行;如索引 0 1 2 3 对应上图左侧方案;
- cols中的元素:存放的是正确方案的列,如元素值 [1 3 0 2]。
这样保存结果,所有皇后自然不在一行上,只需要再判断是否在同一列和两条对角线上即可。
对于对角线上的判断,只需要判断横纵坐标之差是否相等即可。(比如 点(x1, y1) 和 点(x2,y2), 在对角线上的条件是 abs(x1 - x2) == abs(y1 - y2)) ; 对应文中代码 abs(i - row) == abs(cols[i] - col) 。其他同求无重复数组排列一致。
class Solution {
public:
vector solveNQueens(int n) {
vector result;
if (n == 0) {
return result;
}
vector cols; // 特别注意:存放正确的解决方法,cols中的元素:存放的是正确方案的列,cols中元素的索引:存放的是对应的行 //这样保存结果,所有皇后自然不在一行上,只需要再判断是否在同一列和两条对角线上即可
backTracking(n, result, cols);
return result;
}
void backTracking(int n, vector& result, vector cols) { //cols也可引用传递
if (cols.size() == n) {
result.push_back(draw(cols));
return; // 该句最好加上,不加也能测试通过
}
for (int col = 0; col < n; col++) { // 遍历每一列,找到符合条件的列
if (!isValid(cols, col)) {
continue;
}
cols.push_back(col);
backTracking(n, result, cols);
cols.pop_back();
}
}
bool isValid(vector& cols, int col) {
int row = cols.size(); //特别注意:这里row(cols中目前最后一个元素下一个位置的索引)代表的是将要放入到的行的值
for (int i = 0; i < row; i++) { // 遍历已经记录下来的皇后所在的每一行,进行位置判断
if (cols[i] == col) { //判是否同列: 如果已经放入的皇后所在的列 等于 将要放入的列,就则当前列(col)无效
return false;
}
if (abs(i - row) == abs(cols[i] - col)) { //判是否在两条对角线上: 如果已经放入的皇后位置(i, cols[i])与将要放入的皇后位置(row, col)之间的行差 = 列差,则当前列无效
return false;
}
}
return true;
}
vector draw(vector& cols) {
vector result;
int n = cols.size();
for (int i = 0; i < n; i++) {
string strRow(n, '.'); //特别注意:这里string的初始化方法!
strRow[cols[i]] = 'Q'; // 这里改变string某个位置的值的简单方法。
result.push_back(strRow);
}
return result;
}
};描述: 同上 a,只是最终只要解的个数 (来源:leetcode 52. N皇后 II = lintcode34·N皇后问题(二))
代码
此时只需要一个 int sum = 0; 来保存结果即可。不再需要 vector results 保存所有的可能。
class Solution {
public:
int totalNQueens(int n) {
if (n == 0) {
return 0;
}
int sum = 0; // 待求结果
vector cols;
backTracking(n, sum, cols);
return sum;
}
void backTracking(int n, int& sum, vector cols) {
if (cols.size() == n) {// 返回条件
sum++;
return;
}
for (int col = 0; col < n; col++) {
if (!isValid(cols, col)) {
continue;
}
cols.push_back(col);
backTracking(n, sum, cols);
cols.pop_back();
}
}
bool isValid(vector cols, int col) {
// 同 上一例题 a
}
};


