多边形或轮廓等距离外扩或收缩

 参考：多边形或轮廓等距离外扩或收缩_hjk61314的博客-CSDN博客_多边形外扩

1. 需求

已知：给定一个简单多边形，多边形按照顺时针或者逆时针的数组排列，

求：内部等距离缩小或者外部放大的多边形，该多边形实际上是由距离一系列平行已知多边形的边，并且距离为L（已知）的线段所构成的。如图所示，外围的是原多边形，内侧红色是新的多边形

2. 原理

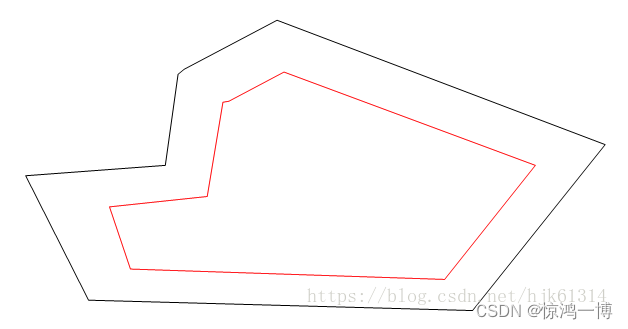
数学描述：多边形的相邻两条边，L1和L2，交于Pi点，做平行于L1和L2，平行线间距是L的，并且位于多边形内部的两条边，交于Qi点，我们要计算出Qi的坐标，如图，

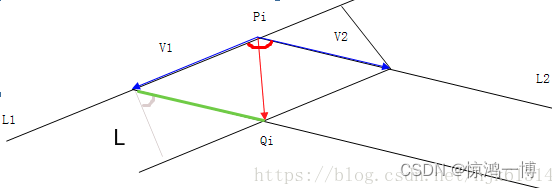PiQi向量，显然是等于平行四边形的两个相邻边的向量v1和v2的和。

而v1和v2向量的方向，就是组成多边形的边的方向，可以用顶点差来表示。

v1和v2向量的长度是相同的，等于平行线间距L与两个线段夹角的sin值的除法。

即： Qi ＝ Pi ＋ (v1 + v2)

    Qi = Pi + L / sinθ * ( Normalize(v2) + Normalize(v1))

    Sin θ = |v1 × v2 | /|v1|/|v2| （叉乘的性质）

其中，L / sinθ为平行四边形的边长（绿色线段，向量v1 v2对应的长度）

知识点：

1. 向量a=(x,y)的模长等于

2. 向量积或者叫叉乘: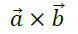

其运算结果仍是一个向量，我们记之为向量c，它的模定义为：

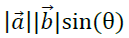
3. 二维向量的叉积：

定义：叉乘是向量间的一种运算，设两个向量分别为,，那么它们的叉乘就为，

计算步骤：

• ⑴、获取多边形顶点数组PList;
• ⑵、计算DPList[Vi+1-Vi];
• ⑶、单位化NormalizeDPList,得到NDP[DPi];（用同一个数组存储）
• ⑷、Sinα = Dp(i+1) X DP(i);
• ⑸、Qi = Pi + d/sinα (NDPi+1-NDPi)
• ⑹、这样一次性可以把所有顶点计算完。

注意，交换Qi表达式当中NDPi+1-NDPi的顺序就可以得到外部多边形顶点数组。

2. 实现

#include 
#include 
#include 
#include  
#include 

#include 
#include 
#include 

#include 

using namespace cv;
using namespace std;

void expand_polygon(vector &pList, vector &out){// already ordered by anticlockwise

    // 1. vertex set
    // pList

    // 2. edge set and normalize it
    vector dpList, ndpList;
    int count = pList.size();
    for(int i = 0; i < count; i++){
        int next = (i==(count-1) ? 0: (i+1));
        dpList.push_back(pList.at(next)-pList.at(i));
        float unitLen = 1.0f/sqrt(dpList.at(i).dot(dpList.at(i)));
        ndpList.push_back(dpList.at(i) * unitLen);
        cout