【洛谷】【动态规划】P1002 [NOIP2002 普及组] 过河卒

题目链接：https://www.luogu.com.cn/problem/P1002

题目描述

  棋盘上 A点有一个过河卒，需要走到目标 B点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

  棋盘用坐标表示，A 点 (0, 0)、B点 (n, m)，同样马的位置坐标是需要给出的。

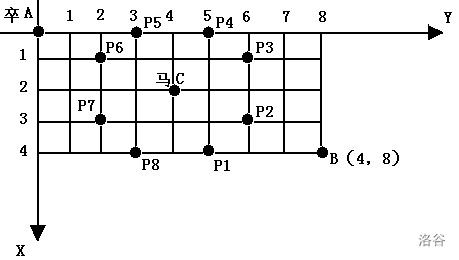
  现在要求你计算出卒从 A 点能够到达 B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

  一行四个正整数，分别表示 B点坐标和马的坐标。

输出格式

  一个整数，表示所有的路径条数。

测试样例

输入
6 6 3 3
输出
6

解题思路

1.首先我们要明白，哪些点是马可以走到的点，我们针对这个题为例，A为原点，B为目标点，X为马可以走到的点

 A 0 0 0 0 0 0
 0 0 X 0 X 0 0
 0 X 0 0 0 X 0
 0 0 0 M 0 0 0
 0 X 0 0 0 X 0
 0 0 X 0 X 0 0
 0 0 0 0 0 0 B

2.在这里我们发现，马的行动范围在[2,2]以内，如果我们直接用状态转移的话，在i-1和j-1的时候就会发生数组越界，所以我们在这里选择的是把所有点的坐标统一加2

3.在计算路径时，我们发现，A只能向右走或者向下走，所以对于每一个点，只需要计算从它左边和上边来的路径之和即可，这就是本题的状态转移方程，如下所示 f [ i ] [ j ] = m a x ( f [ i ] [ j − 1 ] + f [ i − 1 ] [ j ] , f [ i ] [ j ] ) f[i][j] = max( f[i][j-1] + f[i-1][j] , f[i][j] ) f[i][j]=max(f[i][j−1]+f[i−1][j],f[i][j]) 针对本题计算出来的结果如下所示

1 1 1 1 1 1 1
1 0 X 1 X 1 2
1 X 0 1 1 X 2
1 1 1 M 1 1 3
1 X 1 1 0 X 3
1 1 X 1 X 0 3
1 2 2 3 3 3 6

AC代码

#include
#include
using namespace std;

int main()
{
    int bx,by,mx,my;
    cin>>bx>>by>>mx>>my;
    //加2避免马的影响
    bx+=2; by+=2;
    mx+=2; my+=2;
    //这里一定记得是long long，要不然会WA的！
    long long area[30][30]={0};
    bool ma[30][30]={0};
    int x[]={0,-2,-1,1,2,-2,-1,1,2};
    int y[]={0,1,2,2,1,-1,-2,-2,-1};
    //把马能走的位置设为1，后续方便判断
    for(int i=0;i