LeetCode岛屿的最大面积

剑指 Offer II 105. 岛屿的最大面积

给定一个由 0 和 1 组成的非空二维数组 grid ，用来表示海洋岛屿地图。

一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

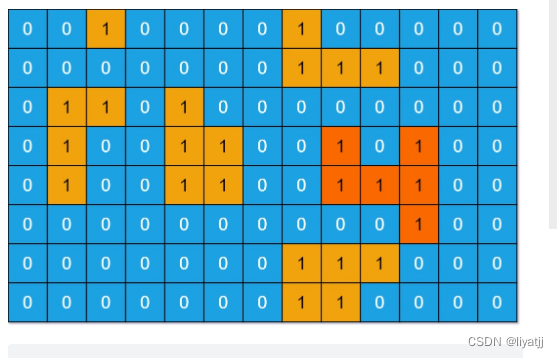
输入: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,1,1,0,1,0,0,0,0,0,0,0,0], [0,1,0,0,1,1,0,0,1,0,1,0,0], [0,1,0,0,1,1,0,0,1,1,1,0,0], [0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出: 6 解释: 对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

来源：力扣（LeetCode）

对于每一个小方块而言，去搜寻它的上下左右四个方向去寻找和它同为1并且相邻的方块，记录相应个数，最后取最大值。

深度优先搜索：

1.由于岛屿的设定是一定得是1，所以可以先增加一个判断条件，当值是0的时候就可以直接返回0。 （1）由于要考虑到数组越界问题，所以当边界的元素搜索到边界以外的元素时需要返回0，这个时候其实就是数组下标越界的时候。 （2）当i和j在四个角落时有的方向上i和j有可能是负数，所以还要增加判断条件，当i或j为负数时可以直接返回0

2.如果不是，它本身就应该算数，所以先定义一个ans记录个数，初值应该是1，而且位置应该在判断条件之后。

3.然后向四个方向进行检查，这里采用的是利用数组的方式： 分析规律可得其 右侧元素：i不变，j+1 左侧元素：i不变，j-1 下方元素：i+1，j不变 上方元素：i-1，j不变 所以可以得到两个标记下标变化的两个数组 di【】{0，0，1，-1} dj【】{1，-1，0，0} 每次要进行新方向的扩展就直接加上对应下标就可以，哪个下标在前无所谓，因为会四个方向都遍历到。 当遍历到的比如说这个元素的左侧元素是0，那么就会ans返回0，也就是对岛屿个数没影响，而且也不会再接着遍历这个0元素的其他方向。

4.在四个方向的遍历中可以使用递归的思想，最终某个岛屿的ans就应该是全部方块为1的个数和，也就是ans+=dfs（res，nexti，nextj）

5.其实每次向某个方向走，就是看看那个方向上是否是1，所以每次ans应该返回的不是0就是1，全都加起来就是某个岛屿的ans。

6.在主函数里面当然要对每一个方块进行检索，并且不断更新ans的值即可。

class Solution {
    public int maxAreaOfIsland(int[][] grid) {

        int ans=0;
        for(int i=0;i