LeetCode二维子矩阵的和

剑指 Offer II 013. 二维子矩阵的和

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。 实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化 int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。

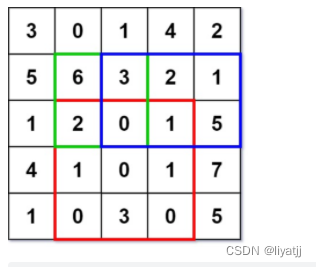
输入: [“NumMatrix”,“sumRegion”,“sumRegion”,“sumRegion”] [[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]] 输出: [null, 8, 11, 12]

解释: NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]); numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和) numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和) numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

来源：力扣（LeetCode）

一开始想的是用暴力解法，编译通过了，但是当要求和的次数很多的时候就会降低效率。

采用求前缀和的方法，新建一个sum数组，sum数组与matrix行数相同，但是列数多一列，用来存储前面元素的加和。 例如 sum【0】【1】=sum【0】【0】+matrix【0】【0】=3 sum【0】【2】=sum【0】【1】+matrix【0】【1】=3+0=3 等等 这样就可以得到某行某列的sum值分别对应前面几个值的加和，当要计算例如红色矩阵里面的第一行时，只需要用右上角右侧的元素的sum减去左上角元素的sum值即可。 再将三行的sum值进行相加，就能得到最终的ans。

class NumMatrix {

    int[][] sum;
    public NumMatrix(int[][] matrix) {
        int x=matrix.length,y=matrix[0].length;
        sum = new int[x][y+1];
        for(int i=0;i