目录
介绍
问题陈述
线性动态系统
离散时间
线性案例的解决方案
线性案例解决方案的探讨
非线性系统
方法限制
不断反馈
软件的使用
数字示例
线性系统
范德波尔(Van der Pol)振荡器
具有标量控制的Rayleigh方程
具有常数反馈的非线性系统
双连杆机器人操纵器
结论
附录
- 下载源代码 - 35.2 KB
在本文中，我想介绍一种紧凑且易于使用的软件工具，以实现对动态系统的最佳控制。最佳控制是一个非常广泛的主题。其基础是由Richard Bellman，Lev Pontryagin，Rudolf Kalman等人在20世纪50年代末至60年代奠定的。最佳控制具有许多实际应用。在这里，我们将重点关注以下经典的最优控制问题。我们的目标是通过外部控制输入将给定的动态系统从初始状态转移到某个最终状态。我们希望在此过渡期间系统参数尽可能接近其规定的轨迹。这是具有许多实际应用的最佳控制的非常基本的任务。例如，启动电动机将电流的初始跳跃限制在可接受的值。
处理这个问题甚至它的陈述需要大量的数学。我将仅限于描述问题所需的最低要求，并了解如何使用软件。附录中给出了一些额外的递归公式，没有证明。
问题陈述让我们正式化我们的问题。动态系统用以下微分方程组描述：
（1）
其中t是时间，x是状态向量，由表征系统行为的参数组成，ẋ是x的一阶导数的向量，m是控制向量。通常，控制矢量的维度不超过状态矢量的维度。在该语句中，向量m独立于向量x，并且可以被认为是开环系统的控制。具有输入控制向量m和状态向量x的开环控制系统如下所示：
开环控制系统
我们希望在0到t f的最终时间之间的时间间隔内获得控制策略m（t），这最小化了成本函数。
（2）
其中上标T表示矢量或矩阵的转置，r是期望的状态向量，u是期望的控制向量，Q和Z分别是用于状态和控制向量的期望参数和实际参数之间的偏差的权重矩阵。在大多数情况下Q和Z.是对角矩阵（但不一定！）。它们的每个对角线元素定义在给定时刻参数的期望值和实际值之间的差的平方的相对权重。矩阵可以是时间依赖的，例如，通常的做法是在最后时间增加差异的相对权重以确保期望的最终状态。这里提出的问题通常被称为“跟踪问题”。
线性动态系统在我们找到解决方案之前，让我们讨论动态系统的一个特例。研究最充分的系统类是线性动态系统，即用一组线性微分方程描述动力学的系统。对于这样的系统，等式（1）可以重写如下：
（3）
其中A(t) 和B(t) 是矩阵。首先，我们将为这类系统提供解决方案，然后将其扩展到非线性动态系统。
离散时间由于我们将提供数字解决方案，我们将在离散的时刻处理系统。因此，我们将重新设计离散时间t = k·Δt的问题，其中Δt构成一个小的时间间隔（采样间隔），k是给定的时间步长，0 mu * x[1] * (1 - x[0] * x[0]) - x[0] + m[0] }; // Exact formulas for gradients calculation var gradientsA = new CalcDelegate[dimensionX, dimensionX]; gradientsA[0, 0] = (k, deltaT, m, x) => 0; gradientsA[0, 1] = (k, deltaT, m, x) => 1; gradientsA[1, 0] = (k, deltaT, m, x) => -1 - 2 * x[0] * x[1]; gradientsA[1, 1] = (k, deltaT, m, x) => 1 - x[0] * x[0]; var gradientsB = new CalcDelegate[dimensionX, dimensionM]; gradientsB[0, 0] = (k, deltaT, m, x) => 0; gradientsB[1, 0] = (k, deltaT, m, x) => 1; var dynamicSystem1 = SQ.Create(functions, gradientsA, gradientsB, Q, Z, r, u, xInit, dt, N, (currCost, prevCost, iteration) => iteration > 20); dynamicSystem1.RunOptimization(); dynamicSystem1.Output2Csv("VanDerPol_ExactGrads", lstFormatting); dynamicSystem1.OutputExecutionDetails(isExactGradient: true); // Numeric gradients calculation double delta = 0.1; var dynamicSystem2 = SQ.Create(functions, new Vector(dimensionM, delta), new Vector(dimensionX, delta), Q, Z, r, u, xInit, dt, N, (currCost, prevCost, iteration) => iteration > 20); dynamicSystem2.RunOptimization(); dynamicSystem2.Output2Csv("VanDerPol_NumGrads", lstFormatting); dynamicSystem2.OutputExecutionDetails(isExactGradient: false); Console.WriteLine($"End \"{TITLE}\"{Environment.NewLine}{Environment.NewLine}"); } 数字示例 线性系统
有一个机械系统：质量M通过力移动。根据牛顿第二定律，力等于质量和加速度的乘积的结果，这是位移的二阶导数。让我们将差异表示为x 0，将速度表示为x 1，将力表示为m 0。系统采用以下二阶矩阵微分方程进行描述：
ẋ= Ax + Bm，其中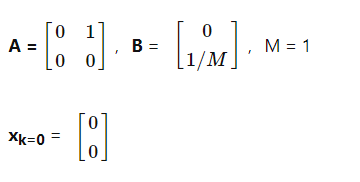
成本函数是
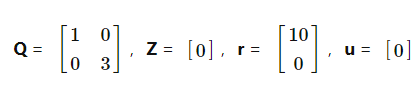
Δt= 1，N = 41。
线性系统的瞬态
由计算得到的闭环输入和反馈因子是
输入4.48，
反馈：从x 0 -0.448和x 1 -1.22。
范德波尔(Van der Pol)振荡器这是一个非线性系统。我们的目标是平稳，快速地抑制正在进行的振荡。
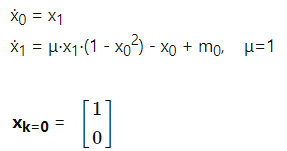
成本函数是
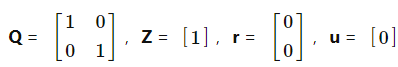
Δt= 0.1，N = 51。
20次迭代后受控Van der Pol振荡器的瞬变
控制策略m针对不同的迭代次数（1,2,3和20）
不同迭代次数的成本函数差异（百分比）
在上述具有所选状态和控制矢量和权重矩阵的情况下，我们观察到良好的收敛迭代计算。
具有标量控制的Rayleigh方程这是另一种非线性振荡系统。我们的目标与之前的情况相同：平稳和快速的持续振荡阻尼。
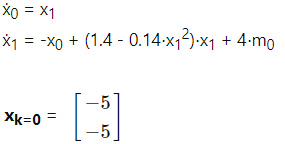
成本函数是
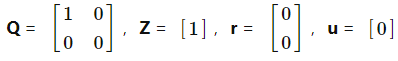
Δt= 0.025，N = 101。
94次迭代后的瞬态
控制策略m用于不同的迭代次数（1,2,3和94）
不同迭代次数的成本函数差异（百分比）
与Van der Pol振荡器类似，在这种情况下，虽然需要更多的迭代来将成本函数变为零，但也实现了良好的方法收敛。
具有常数反馈的非线性系统这是一个非线性系统，可以使用恒定反馈从其给定的初始状态充分转换为零状态。
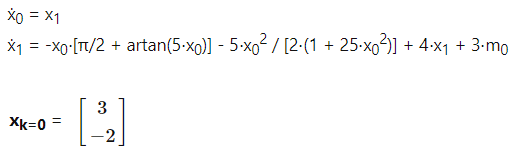
成本函数是
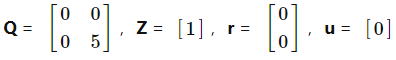Δt= 0.1，N = 101。
单次迭代的瞬态
计算结果得到的反馈因子是
从X 0 0.09 0≅和从X 1 -2.29。
瞬变 m0 =-3⋅x 1
对于单次迭代，m 0 对 x 1
上图描绘了使用我们的软件针对单次迭代后选择的权重矩阵计算的瞬态，以及针对平滑转换的特殊选择的“理想”反馈的瞬态。最后一个图显示了我们计算的受控状态坐标x 1和控制m 0之间的关系。通过我们的软件计算出的控制看起来更具“攻击性”，在m 0和x 1中具有小的过冲，但是完全可以接受。
双连杆机器人操纵器在这篇文章中（英文）介绍了所描述的技术在双连杆机器人操纵器的最佳控制中的应用。
代码示例中提供了更多数字示例。
结论本文简要解释了线性和非线性系统的序列二次优化控制问题的数值解。接近的拟线性化用于将线性化系统的非线性问题减少为一组连续的线性二次问题。提供紧凑且易于使用的软件及其使用示例。
附录用于计算反向运行中的控制向量m的递归方程（7）中的参数c和L可以从动态编程方程（本文的格式不允许提供适当的数学变换）获得，作为以下递归操作的集合：
其中P和v分别是递归计算的辅助矩阵和向量，k从k = N-1开始，其中P 0=0，v 0= 0。
注意，上述计算需要根据传递矩阵H，权重矩阵和矩阵P来反转辅助W矩阵。
原文地址：https://www.codeproject.com/Articles/863257/Simple-Software-for-Optimal-Control
