实现机器学习的循序渐进指南II——决策树

目录

介绍

决策树模型

特征选择

决策树的生成

分类

结论与分析

可访问 实现机器学习的循序渐进指南系列汇总，获取本系列完成文章列表。 

介绍

决策原则并不复杂。从根节点开始，将节点中存储的特征值与测试对象的相应特征值进行比较。然后，根据比较结果递归地转向左子树或右子树。最后，叶节点的标签是测试对象的预测。

例如，下面有一个决策树，其中功能集是{hungry, money}，标签集是{go to restaurant, go to buy a hamburger, go to sleep}。

在决策过程中，首先，如果我饿了，转向右侧的子树，这意味着我会去睡觉。否则转向左侧子树。然后，检查我的钱包里有多少钱。如果我有超过25美元，我会去餐厅。否则，我只能去买一个汉堡包。

决策树模型

决策树模型由特征选择，决策树的生成和分类组成。

特征选择

特征选择的目的是选择具有训练数据分类能力的特征，以使学习过程更有效。特征选择包括两部分，即特征选择和特征值选择。选定的元组（特征，特征值）将作为决策树中的节点应用。

特征选择通常基于信息增益或信息增益比。信息增益定义为在选择特征A，时，集合D，的经验熵与条件熵之间的差异，计算如下：

具体地，当数据集D被特征A划分为两个子集时，信息增益表示为：

其中是第一个子集的比例，即：

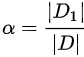
信息增益的计算代码如下所示：

left_set, right_set = self.divideData(data, i, value)
# calculate information gain
ratio = float(len(left_set)/sample_num)
if ratio == 0.0:
    info_gain = init_entropy - (1 - ratio) * self.getEntropy(right_set[:, -1])
elif ratio == 1.0:
    info_gain = init_entropy - ratio*self.getEntropy(left_set[:, -1])
else:
    info_gain = init_entropy - ratio *
    self.getEntropy(left_set[:, -1]) - (1 - ratio) * self.getEntropy(right_set[:, -1])

到目前为止，我们已经学会了如何计算信息增益。但是，如何计算经验熵？经验熵是训练集标签的熵，由下式给出：

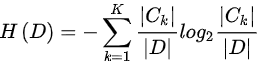
上面的等式看起来有点复杂，但很容易实现。我们来看看它的代码：

def getEntropy(self, labels):
    labels_num = len(labels)
    label_count = self.uniqueCount(labels)

    entropy = 0.0
    for j in label_count:
        prop = label_count[j]/labels_num
        entropy = entropy + (-prop*math.log(prop, 2))

    return entropy

决策树的生成

有许多算法可以生成决策树，例如ID3，C4.5。在本文中，我们以ID3算法为例生成决策树。

首先，让我们弄清楚特征选择后的分割过程。我们知道，特征选择是使数据可分类。因此，分割过程是根据所选择的特征index 及其选择的值value来划分训练数据。具体来说，拆分过程是如果样本中的特征值index大于value，则将样本添加到右子树中并删除样本中的index特征; 否则，如果样本中的特征值index小于value，则将样本添加到左子树中并删除样本中的index特征。拆分过程的代码是：

def divideData(self, data, index, value):
    left_set = []
    right_set = []
    # select feature in index with value
    for temp in data:
        if temp[index] >= value:
            # delete this feature
            new_feature = np.delete(temp, index)
            right_set.append(new_feature)
        else:
            new_feature = np.delete(temp, index)
            left_set.append(new_feature)
    return np.array(left_set), np.array(right_set)

在生成决策树之前，我们定义一个数据结构以将节点保存在决策树中：

class DecisionNode:
    def __init__(self, index=-1, value=None, results=None, right_tree=None, left_tree=None):
        self.index = index                    # the index of feature
        self.value = value                    # the value of the feature with index
        self.results = results                # current decision result
        self.right_tree = right_tree
        self.left_tree = left_tree

然后，我们可以递归地生成决策树。如果数据集中没有任何特征，请停止。如果信息增益小于给定阈值，请停止。否则，根据最佳选择的特征及其值拆分数据集，如下所示：

def createDecisionTree(self, data):
   # if there is no feature in data, stop division
   if len(data) == 0:
       self.tree_node = DecisionNode()
       return self.tree_node

   best_gain = 0.0
   best_criteria = None
   best_set = None

   feature_num = len(data[0]) - 1
   sample_num = len(data[:, -1])
   init_entropy = self.getEntropy(data[:, -1])

   # get the best division
   for i in range(feature_num):
       uniques = np.unique(data[:, i])
       for value in uniques:
           left_set, right_set = self.divideData(data, i, value)
           # calculate information gain
           ratio = float(len(left_set)/sample_num)
           if ratio == 0.0:
               info_gain = init_entropy - (1 - ratio) * self.getEntropy(right_set[:, -1])
           elif ratio == 1.0:
               info_gain = init_entropy - ratio*self.getEntropy(left_set[:, -1])
           else:
               info_gain = init_entropy - ratio * self.getEntropy
                 (left_set[:, -1]) - (1 - ratio) * self.getEntropy(right_set[:, -1])
           if info_gain > best_gain:
               best_gain = info_gain
               best_criteria = (i, value)
               best_set = (left_set, right_set)

   # create the decision tree
   if best_gain < self.t:
       self.tree_node = DecisionNode(results=self.uniqueCount(data[:, -1]))
       return self.tree_node
   else:
       ltree = self.createDecisionTree(best_set[0])
       rtree = self.createDecisionTree(best_set[1])
       self.tree_node = DecisionNode(index=best_criteria[0],
                        value=best_criteria[1], left_tree=ltree, right_tree=rtree)
       return self.tree_node

分类

分类原理就像二进制排序树，即将节点中存储的特征值与测试对象的相应特征值进行比较。然后，递归转向左子树或右子树，如下所示：

def classify(self, sample, tree):
    if tree.results != None:
        return tree.results
    else:
        value = sample[tree.index]
        branch = None
        if value >= tree.value:
            branch = tree.right_tree
        else:
            branch = tree.left_tree
        return self.classify(sample, branch)

结论与分析

在生成决策树之后，通过动态编程存在修剪过程以获得最佳决策树。此外，分类和回归树（CART）是一种决策树，不仅可以应用于分类，还可以应用于回归。最后，让我们将决策树与Sklearn中的树进行比较，检测性能如下所示：

从图中我们可以了解到决策树不如sklearn那么好，这可能是我们不应用修剪过程。

可以在MachineLearning中找到本文中的相关代码和数据集。

有兴趣的小伙伴可以查看上一篇或者下一篇。

 

原文地址：https://www.codeproject.com/Articles/4047359/Step-by-Step-Guide-To-Implement-Machine-Learning-2