实现机器学习的循序渐进指南IX ——树回归

目录

介绍

回归模型

特征选择

回归树的生成

回归

结论与分析

可访问 实现机器学习的循序渐进指南系列汇总，获取本系列完成文章列表。 

介绍

在现实世界中，一些关系不是线性的。因此，应用线性回归分析这些问题是不合适的。为了解决这个问题，我们可以采用树回归。树回归的主要思想是将问题分成较小的子问题。如果子问题是线性的，我们可以结合所有子问题模型来获得整个问题的回归模型。

回归模型

树回归类似于决策树，它由特征选择，回归树的生成和回归组成。

特征选择

在决策树中，我们根据信息增益选择特征。但是，对于回归树，预测值是连续的，这意味着回归标签对于每个样本几乎是唯一的。因此，经验熵缺乏表征能力。因此，我们利用平方误差作为特征选择的标准，即

 

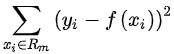
其中R m是由回归树除以的空间，f（x）由下式给出

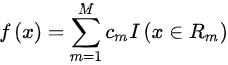
因此，无论样本的特征是什么，相同空间中的输出都是相同的。R m 的输出是空间中所有样本的回归标签的平均值，即

回归树的特征选择类似于决策树，旨在最小化损失函数，即

回归树的生成

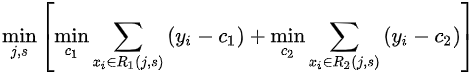
我们首先定义一个数据结构来保存树节点

class RegressionNode():    
    def __init__(self, index=-1, value=None, result=None, right_tree=None, left_tree=None):
        self.index = index
        self.value = value
        self.result = result
        self.right_tree = right_tree
        self.left_tree = left_tree

像决策树一样，假设我们选择了最佳特征及其对应的值（j，s），那么我们将数据溢出

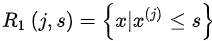
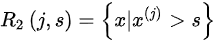
并且每个二进制文件的输出是 

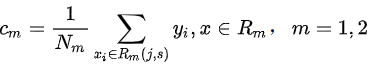
回归树的生成与决策树的生成几乎相同，此处不再赘述。您可以阅读实现机器学习的循序渐进指南II——决策树以获取更多详细信息。

def createRegressionTree(self, data):
    # if there is no feature
    if len(data) == 0:
        self.tree_node = treeNode(result=self.getMean(data[:, -1]))
        return self.tree_node

    sample_num, feature_dim = np.shape(data)

    best_criteria = None
    best_error = np.inf
    best_set = None
    initial_error = self.getVariance(data)

    # get the best split feature and value
    for index in range(feature_dim - 1):
        uniques = np.unique(data[:, index])
        for value in uniques:
            left_set, right_set = self.divideData(data, index, value)
            if len(left_set) < self.N or len(right_set) < self.N:
                continue
            new_error = self.getVariance(left_set) + self.getVariance(right_set)
            if new_error < best_error:
                best_criteria = (index, value)
                best_error = new_error
                best_set = (left_set, right_set)

    if best_set is None:
        self.tree_node = treeNode(result=self.getMean(data[:, -1]))
        return self.tree_node
    # if the descent of error is small enough, return the mean of the data
    elif abs(initial_error - best_error) < self.error_threshold:
        self.tree_node = treeNode(result=self.getMean(data[:, -1]))
        return self.tree_node
    # if the split data is small enough, return the mean of the data
    elif len(best_set[0]) < self.N or len(best_set[1]) < self.N:
        self.tree_node = treeNode(result=self.getMean(data[:, -1]))
        return self.tree_node
    else:
        ltree = self.createRegressionTree(best_set[0])
        rtree = self.createRegressionTree(best_set[1])
        self.tree_node = treeNode(index=best_criteria[0], value=best_criteria[1], left_tree=ltree, right_tree=rtree)
        return self.tree_node

回归

回归原理就像二进制排序树，即将节点中存储的特征值与测试对象的相应特征值进行比较。然后，递归转向左子树或右子树 ，如下所示：

def classify(self, sample, tree):
    if tree.result is not None:
        return tree.result
    else:
        value = sample[tree.index]
        if value >= tree.value:
            branch = tree.right_tree
        else:
            branch = tree.left_tree
        return self.classify(sample, branch)

结论与分析

分类树和回归树可以组合为分类和回归树（CART）。实际上，在生成树后生成树时存在修剪过程。我们跳过它们是因为它有点复杂而且并不总是有效。最后，让我们将回归树与Sklearn中的树进行比较，检测性能如下所示：

Sklearn树回归性能：

我们的树回归性能：

 

我们的树回归需要比sklearn更长的时间。

可以在MachineLearning中找到本文中的相关代码和数据集  。

有兴趣的小伙伴可以查看上一篇和下一篇。

 

原文地址：https://www.codeproject.com/Articles/5061172/Step-by-Step-Guide-to-Implement-Machine-Learning-7