目录
通过函数表示数据
集合
空集
全集
单元素集
其他集合
二元操作
并集
交集
笛卡尔积
差集
对等差分
其他操作
对于那些想要更进一步的人
欧几里得平面
绘制磁盘
绘制水平和垂直半平面
函数
对于那些想要更进一步的人
分形
复数和绘图
牛顿分形
对于那些想要更进一步的人
延迟简介
- 下载源码 - 121.6 KB

通过函数表示数据
让S是任何元素a,b,c...(例如,桌子上的书,或者欧几里得平面的点)的集合,并让S'是这些元素的任意子集(例如,桌子上的绿皮书,或者半径为1的圆上以欧几里得平面原点为中心的点)。
集合S'的特征函数S'(x)是一个函数,它将true或false与S的每个元素x相关联。
S'(x) = true if x is in S'
S'(x) = false if x is not in S'让S成为桌子上的一套书,让S'成为桌上的绿皮书。让a和b是两个绿色的书,让c和d是在表中的两个红色的本。然后:
S'(a) = S'(b) = true
S'(c) = S'(d) = false让S是欧几里德平面中的点的集合,并且让S'在半径为1的园中以欧几里得平面(0,0)原点为中心的点的集合(单位圆)。让a和b在单位圆的两点,并让c并且d是半径为2的圆上以欧几里得平面原点为中心的点。然后:
S'(a) = S'(b) = true
S'(c) = S'(d) = false因此,任何集合S'总是可以由其特征函数表示。一个函数,它将一个元素作为参数,并返回true如果该元素在S'中,否则返回false。换句话说,可以通过C#中的谓词来表示集合(抽象数据类型)。
Predicate set;在接下来的部分中,我们将看到如何通过C#以函数方式表示集合代数中的一些基本集合,然后我们将在集合上定义泛型二进制运算。然后,我们将在欧几里德平面的子集上对数字应用这些操作。集合是抽象数据结构,数字的子集和欧几里得平面的子集是抽象数据结构的表示,最后二元操作是适用于抽象数据结构的任何表示的通用逻辑。
集合本节通过C#介绍集合代数中一些基本集的表示。
空集
让E是空集和Empty是它的特征函数。在集合的代数中,E是没有元素的唯一集合。因此,Empty可以定义如下:
Empty(x) = false if x is in E
Empty(x) = false if x is not in E因此,E在C#中的表示可以定义如下:
public static Predicate Empty()
{
return x => false;
}在集合的代数中,Empty表示如下:
![]()
因此,运行以下代码:
Console.WriteLine("\nEmpty set:");
Console.WriteLine("Is 7 in {{}}? {0}", Empty()(7));结果如下:

全集

让S是一集合和S'是包含所有要素的S的子集,All是其特色函数。在集合的代数中,S'是包含所有元素的完整集合。因此,All可以这样定义:
All(x) = true if x is in S因此,S'在C#中的表示可以定义如下:
public static Predicate All()
{
return x => true;
}在集合的代数中,All表示如下:
![]()
因此,运行以下代码:
Console.WriteLine("Is 7 in the integers set? {0}", All()(7));结果如下:

单元素集
让E是单元素集并且Singleton是它的特征函数。在集合的代数中,E也称为单元集合,或者1元组是具有恰好一个元素e的集合。因此,Singleton可以定义如下:
Singleton(x) = true if x is e
Singleton(x) = false if x is not e因此,E在C#中的表示可以定义如下:
public static Predicate Singleton(T e)
{
return x => e.Equals(x);
}因此,运行以下代码:
Console.WriteLine("Is 7 in the singleton {{0}}? {0}", Singleton(0)(7));
Console.WriteLine("Is 7 in the singleton {{7}}? {0}", Singleton(7)(7));结果如下:

本节介绍整数集的子集。
偶数
让E是一个偶数集合,并且Even是它的特征函数。在数学中,偶数是一个2的倍数。因此,Even可以定义如下:
Even(x) = true if x is a multiple of 2
Even(x) = false if x is not a multiple of 2因此,E在C#中的表示可以定义如下:
Predicate even = i => i % 2 == 0;因此,运行以下代码:
Console.WriteLine("Is {0} even? {1}", 99, even(99));
Console.WriteLine("Is {0} even? {1}", 998, even(998));结果如下:

奇数
让E是一个奇数集合并且Odd是它的特征函数。在数学中,奇数是一个不是2的倍数的数字。因此,Odd可以定义如下:
Odd(x) = true if x is not a multiple of 2
Odd(x) = false if x is a multiple of 2因此,E在C#中的表示可以定义如下:
Predicate odd = i => i % 2 == 1;因此,运行以下代码:
Console.WriteLine("Is {0} odd? {1}", 99, odd(99));
Console.WriteLine("Is {0} odd? {1}", 998, odd(998));结果如下:

3的倍数
让E是一个3的倍数的集合兵器MultipleOfThree是它的特征函数。在数学中,3的倍数是可被3整除的数。因此,MultipleOfThree可以定义如下:
MultipleOfThree(x) = true if x is divisible by 3
MultipleOfThree(x) = false if x is not divisible by 3因此,E在C#中的表示可以定义如下:
Predicate multipleOfThree = i => i % 3 == 0;因此,运行以下代码:
Console.WriteLine("Is {0} a multiple of 3? {1}", 99, multipleOfThree(99));
Console.WriteLine("Is {0} a multiple of 3? {1}", 998, multipleOfThree(998));结果如下:

5的倍数
让E是5的倍数的集合兵器MultipleOfFive是它的特征函数。在数学中,5的倍数是可被5整除的数。因此,MultipleOfFive可以定义如下:
MultipleOfFive(x) = true if x is divisible by 5
MultipleOfFive(x) = false if x is not divisible by 5因此,E在C#中的表示可以定义如下:
Predicate multipleOfFive = i => i % 5 == 0;因此,运行以下代码:
Console.WriteLine("Is {0} a multiple of 5? {1}", 15, multipleOfFive(15));
Console.WriteLine("Is {0} a multiple of 5? {1}", 998, multipleOfFive(998));结果如下:

质数
很久以前,当我接触Project Euler问题时,我不得不解决以下问题:
By listing the first six prime numbers: 2, 3, 5, 7, 11, and 13,
we can see that the 6th prime is 13.
What is the 10 001st prime number?为了解决这个问题,我首先必须编写一个快速算法来检查给定的数字是否为素数。编写算法后,我编写了一个迭代算法,遍历素数直到找到第10 001个素数。
让E是素数的集合并且Prime是它的特征函数。在数学中,素数是大于1的自然数,除了1和自身之外没有正除数。因此,Prime可以定义如下:
Prime(x) = true if x is prime
Prime(x) = false if x is not prime因此,E在C#中的表示可以定义如下:
Predicate prime = IsPrime;IsPrime是检查给定数字是否为素数的方法。
static bool IsPrime(int i)
{
if (i == 1) return false; // 1 is not prime
if (i < 4) return true; // 2 and 3 are primes
if ((i >> 1) * 2 == i) return false; // multiples of 2 are not prime
if (i < 9) return true; // 5 and 7 are primes
if (i % 3 == 0) return false; // multiples of 3 are not primes
// If a divisor less than or equal to sqrt(i) is found
// then i is not prime
int sqrt = (int)Math.Sqrt(i);
for (int d = 5; d e(x) || f(x);
}如您所见,Union是一组特征函数的扩展函数。所有操作将被定义为集合的特征函数上的扩展函数。从而,运行以下代码:
Console.WriteLine("Is 7 in the union of Even and Odd Integers Set? {0}", Even.Union(Odd)(7));结果如下:

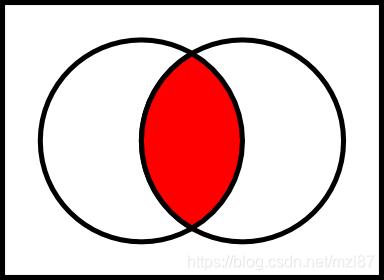
让E和F两个集合。E和F的交集,由E n F表示的是所有元素的集合,他们是E和F的成员。
让Intersection成为交叉操作。因此,可以在C#中实现如下Intersection操作:
public static Predicate Intersection(this Predicate e, Predicate f)
{
return x => e(x) && f(x);
}如您所见,Intersection是一组特征函数的扩展函数。从而,运行以下代码:
Predicate multiplesOfThreeAndFive = multipleOfThree.Intersection(multipleOfFive);
Console.WriteLine("Is 15 a multiple of 3 and 5? {0}", multiplesOfThreeAndFive(15));
Console.WriteLine("Is 10 a multiple of 3 and 5? {0}", multiplesOfThreeAndFive(10));结果如下:

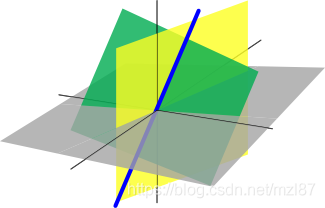
让E和F两个集合。E和F的笛卡儿积,用E × F表示的是所有有序对(e, f) 集合,因此e是E的成员,f是F的成员。
让CartesianProduct成为笛卡尔积操作。因此,CartesianProduct可以在C#中实现如下操作:
public static Func CartesianProduct(this Predicate e, Predicate f)
{
return (x, y) => e(x) && f(y);
}如您所见,CartesianProduct是一组特征函数的扩展函数。从而,运行以下代码:
Func cartesianProduct = multipleOfThree.CartesianProduct(multipleOfFive);
Console.WriteLine("Is (9, 15) in MultipleOfThree x MultipleOfFive? {0}", cartesianProduct(9, 15));结果如下:

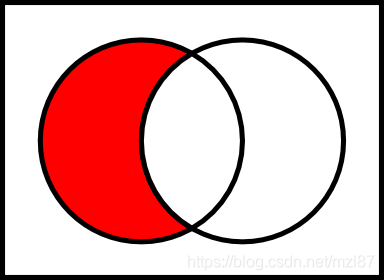
让E和F两个集合。F中E的差集,用E \ F表示的是所有元素的集合,其中的元素是E的成员但不是F的成员。
让Complement成为差集操作。因此,Complement可以在C#中实现如下操作:
public static Predicate Complement(this Predicate e, Predicate f)
{
return x => e(x) && !f(x);
}如您所见,Complement是一个集合的特征函数的扩展方法。从而,运行以下代码:
Console.WriteLine("Is 15 in MultipleOfThree \\ MultipleOfFive set? {0}",
multipleOfThree.Complement(multipleOfFive)(15));
Console.WriteLine("Is 9 in MultipleOfThree \\ MultipleOfFive set? {0}",
multipleOfThree.Complement(multipleOfFive)(9));结果如下:

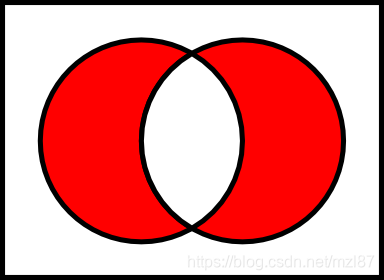
让E和F两个集合。E和F的对等差分,用E ▲ F表示的是所有元素的集合,其中的元素是E和F的成员,但不是E和F的交集成员。
让SymmetricDifference成为对等差分操作。因此,SymmetricDifference可以在C#中以两种方式实现操作。一个简单的方法是使用并和差操作,如下:
public static Predicate SymmetricDifferenceWithoutXor(this Predicate e, Predicate f)
{
return Union(e.Complement(f), f.Complement(e));
}另一种方法是使用XOR二进制操作如下:
public static Predicate SymmetricDifferenceWithXor(this Predicate e, Predicate f)
{
return x => e(x) ^ f(x);
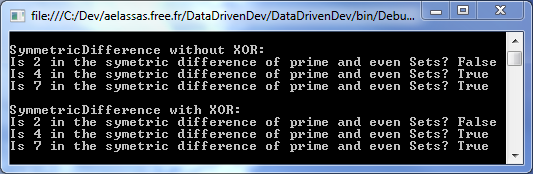
}如您所见,SymmetricDifferenceWithoutXor和SymmetricDifferenceWithXor是集合的特征函数的扩展方法。从而,运行以下代码:
// SymmetricDifference without XOR
Console.WriteLine("\nSymmetricDifference without XOR:");
Predicate sdWithoutXor = prime.SymmetricDifferenceWithoutXor(even);
Console.WriteLine
("Is 2 in the symetric difference of prime and even Sets? {0}", sdWithoutXor(2));
Console.WriteLine
("Is 4 in the symetric difference of prime and even Sets? {0}", sdWithoutXor(4));
Console.WriteLine
("Is 7 in the symetric difference of prime and even Sets? {0}", sdWithoutXor(7));
// SymmetricDifference with XOR
Console.WriteLine("\nSymmetricDifference with XOR:");
Predicate sdWithXor = prime.SymmetricDifferenceWithXor(even);
Console.WriteLine("Is 2 in the symetric difference of prime and even Sets? {0}", sdWithXor(2));
Console.WriteLine("Is 4 in the symetric difference of prime and even Sets? {0}", sdWithXor(4));
Console.WriteLine("Is 7 in the symetric difference of prime and even Sets? {0}", sdWithXor(7));结果如下:
本节介绍集合上其他有用的二进制操作。
包含
让Contains是检查元素是否在集合中的操作。此操作是一个集合的特征函数的扩展函数,它将元素作为参数,如果元素在集合中则返回true,否则返回false。
因此,此操作在C#中定义如下:
public static bool Contains(this Predicate e, T x)
{
return e(x);
}因此,运行以下代码:
Console.WriteLine("Is 7 in the singleton {{0}}? {0}", Singleton(0).Contains(7));
Console.WriteLine("Is 7 in the singleton {{7}}? {0}", Singleton(7).Contains(7));结果如下:

加
让Add是将一个元素添加到集合中的操作。此操作是一个集合的特征函数的扩展函数,它将元素作为参数并将其添加到集合中。
因此,此操作在C#中定义如下:
public static Predicate Add(this Predicate s, T e)
{
return x => x.Equals(e) || s(x);
}因此,运行以下代码:
Console.WriteLine("Is 7 in {{0, 7}}? {0}", Singleton(0).Add(7)(7));
Console.WriteLine("Is 0 in {{1, 0}}? {0}", Singleton(1).Add(0)(0));
Console.WriteLine("Is 7 in {{19, 0}}? {0}", Singleton(19).Add(0)(7));结果如下:

删除
让Remove是从集合中删除元素的操作。此操作是对集合的特征函数的扩展函数,该函数将元素作为参数并将其从集合中移除。
因此,此操作在C#中定义如下:
public static Predicate Remove(this Predicate s, T e)
{
return x => !x.Equals(e) && s(x);
}因此,运行以下代码:
Console.WriteLine("Is 7 in {{}}? {0}", Singleton(0).Remove(0)(7));
Console.WriteLine("Is 0 in {{}}? {0}", Singleton(7).Remove(7)(0));结果如下:

您可以通过函数式编程看到我们在C#中使用集合代数是多么容易。在前面的部分中显示了最基本的定义。但是,如果你想进一步,你可以考虑:
- 关系集
- 抽象代数,如单倍体,群,场,环,K-矢量空间等
- 包含排除原则
- 罗素的悖论
- 康托尔的悖论
- 双向量空间
- 定理和推论
在上一节中,集合的基本概念是在C#中实现的。在本节中,我们将练习在平面点集(欧几里德平面)上实现的概念。
绘制磁盘
磁盘是由圆圈限定的平面的子集。有两种类型的磁盘。封闭的磁盘是包含构成其边界的圆的点的磁盘,而打开的磁盘是不包含构成其边界的圆的点的磁盘。
在本节中,我们将设置特征函数的闭盘,并在WPF应用程序绘制。
要设置特征函数,首先需要一个计算平面中两点之间欧氏距离的函数。该函数实现如下:
public static double EuclidianDistance(Point point1, Point point2)
{
return Math.Sqrt(Math.Pow(point1.X - point2.X, 2) + Math.Pow(point1.Y - point2.Y, 2));
}其中Point是在System.Windows命名空间中定义的struct。这个公式是基于毕达哥拉斯定理。
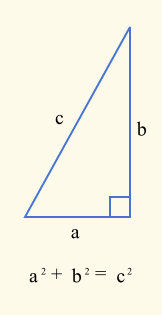
其中c是欧几里德距离,a²是(point1.X - point2.X)²和b²是(point1.Y - point2.Y)²。
让Disk是特征函数的闭盘。在集合的代数中,实数集中的闭盘的定义如下:
![]()
其中a和b是中心和R半径的坐标。
因此,Disk在C#中的实现如下:
public static Predicate Disk(Point center, double radius)
{
return p => EuclidianDistance(center, p) lowerThan ? p.Y = y;
}因此,运行以下代码:
Plan.HorizontalHalfPlane(0, true).Draw(plan);结果如下:
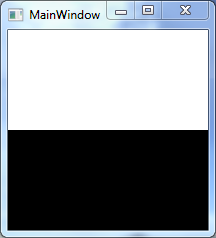
让VerticalHalfPlane是垂直半平面的特征函数。VerticalHalfPlanE在C#中的实现如下:
public static Predicate VerticalHalfPlane(double x, bool lowerThan)
{
return p => lowerThan ? p.X = x;
}因此,运行以下代码:
Plan.VerticalHalfPlane(0, false).Draw(plan);结果如下:
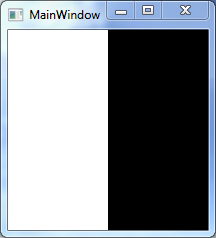
在本文的第一部分中,我们在集合上设置了基本的二元操作。因此,通过组合disk和half-plane的交集,我们可以绘制半磁盘子集。
因此,运行以下示例:
Plan.VerticalHalfPlane(0, false).Intersection(Plan.Disk(new Point(0, 0), 20)).Draw(plan);结果如下:
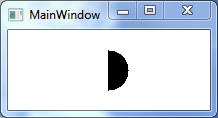
本节介绍欧几里德平面上的集合的函数。
转变
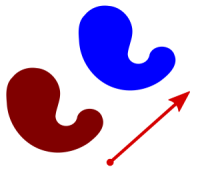
让Translate是转变在平面上的点的函数。在欧几里德几何中,Translate 是一个将给定点在指定方向上移动恒定距离的函数。因此,C#中的实现如下:
public static Func Translate(double deltax, double deltay)
{
return p => new Point(p.X + deltax, p.Y + deltay);
}其中(deltax, deltay)是转变的常量向量。
让TranslateSet是转化平面中集合的函数。此函数在C#中简单实现如下:
public static Predicate TranslateSet(this Predicate set,
double deltax, double deltay)
{
return x => set(Translate(-deltax, -deltay)(x));
}TranslateSet是集合上的扩展函数。它以deltax作为参数,deltax是第一个欧几里得维度中的delta距离,deltay是第二个欧几里得维度中的delta距离。如果点P(x,y)在集合S中被转变,则其坐标将变为(x',y')=(x + delatx,y + deltay)。因此,点(X ' - delatx,Y' - DELTAY)将始终属于集合S。在集合代数中,TranslateSet称为同构,换句话说,所有转变的集合形成转变组T,其与空间本身同构。这解释了函数的主要逻辑。
因此,在我们的WPF应用程序中运行以下代码:
TranslateDiskAnimation();其中TranslateDiskAnimation描述如下:
private const double Delta = 50;
private double _diskDeltay;
private readonly Predicate _disk = Plan.Disk(new Point(0, -170), 80);
private void TranslateDiskAnimation()
{
DispatcherTimer diskTimer = new DispatcherTimer { Interval = new TimeSpan(0, 0, 0, 1, 0) };
diskTimer.Tick += TranslateTimer_Tick;
diskTimer.Start();
}
private void TranslateTimer_Tick(object sender, EventArgs e)
{
_diskDeltay = _diskDeltay set(Scale(-deltax / lambdax, -deltay / lambday, 1 / lambdax, 1 / lambday)(x));
}ScaleSet是集合上的扩展函数。它以deltax作为参数,deltax是第一个欧几里得维度中的delta距离deltay是第二个欧几里得维度中的delta距离,以及(lambdax, lambday)是常数因子向量?如果点P(x,y)在集合S中通过ScaleSet转换,则其坐标将更改为(x',y')=(lambdax*x+delatx,lambday*y+deltay)。因此,点((x’-delatx)/lambdax,(y’-deltay)/lambday)将始终属于集合S,如果?当然,与向量0不同。在集合代数中,ScaleSet称为同构,换句话说,所有同构的集合形成同构群H,同构于空间本身。这解释了函数的主要逻辑。
因此,在我们的WPF应用程序中运行以下代码:
ScaleDiskAnimation();其中ScaleDiskAnimation描述如下:
private const double Delta = 50;
private double _lambdaFactor = 1;
private double _diskScaleDeltay;
private readonly Predicate _disk2 = Plan.Disk(new Point(0, -230), 20);
private void ScaleDiskAnimation()
{
DispatcherTimer scaleTimer = new DispatcherTimer { Interval = new TimeSpan(0, 0, 0, 1, 0) };
scaleTimer.Tick += ScaleTimer_Tick;
scaleTimer.Start();
}
private void ScaleTimer_Tick(object sender, EventArgs e)
{
_diskScaleDeltay = _diskScaleDeltay z * z * z - 2 * z + 2;
}为了能够绘制复数,我需要更新Draw函数。因此,我创建了一个使用ColorMap和ClorTriplet类的Draw函数的重载。下面是C#中的实现。
public static void Draw(this Func fractal, Image plan)
{
var bitmap = new Bitmap((int) plan.Width, (int) plan.Height);
const double reMin = -3.0;
const double reMax = +3.0;
const double imMin = -3.0;
const double imMax = +3.0;
for (int x = 0; x < plan.Width; x++)
{
double re = reMin + x*(reMax - reMin)/plan.Width;
for (int y = 0; y < plan.Height; y++)
{
double im = imMax - y*(imMax - imMin)/plan.Height;
var z = new Complex(re, im);
Complex fz = fractal(z);
if (Double.IsInfinity(fz.Re) || Double.IsNaN(fz.Re) || Double.IsInfinity(fz.Im) ||
Double.IsNaN(fz.Im))
{
continue;
}
ColorTriplet hsv = ColorMap.ComplexToHsv(fz);
ColorTriplet rgb = ColorMap.HsvToRgb(hsv);
var r = (int) Math.Truncate(255.0*rgb.X);
var g = (int) Math.Truncate(255.0*rgb.Y);
var b = (int) Math.Truncate(255.0*rgb.Z);
Color color = Color.FromArgb(r, g, b);
bitmap.SetPixel(x, y, color);
}
}
plan.Source = Imaging.CreateBitmapSourceFromHBitmap(
bitmap.GetHbitmap(),
IntPtr.Zero,
Int32Rect.Empty,
BitmapSizeOptions.FromWidthAndHeight(bitmap.Width, bitmap.Height));
}因此,运行以下代码:
Plan.NewtonFractal().Draw(plan);结果如下:
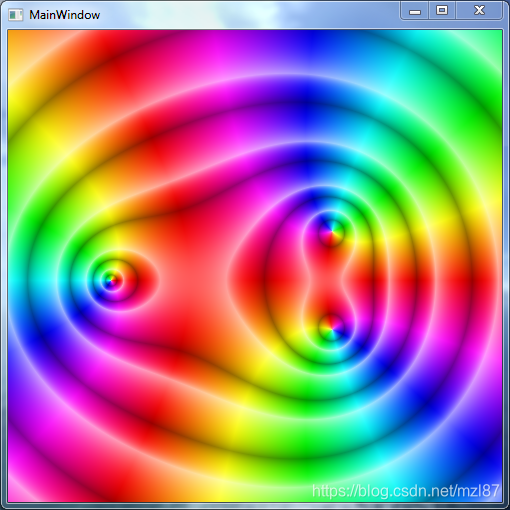
对于那些想要更进一步的人,你可以探索这些:
- Mandelbrot分形
- 朱莉娅分形
- 其他牛顿分形
- 其他分形
在本节中,我们将看到如何从.NET Framework 3.5版开始创建一个Lazy类型。
延迟评估是一种评估策略,它将表达式的评估延迟到需要它的值,并且还避免重复评估。与其他非严格的评估策略(如按名称调用)相比,共享可以通过指数因子减少某些函数的运行时间。下面列出了延迟评估的好处。
- 通过避免不必要的计算以及评估复合表达式的错误条件来提高性能
- 构造潜在无限数据结构的能力:我们可以轻松地创建一个无限的整数集,例如通过一个函数(参见集合部分中素数的例子)
- 将控制流(结构)定义为抽象而不是基元的能力
我们来看看下面的代码:
public class MyLazy
{
#region Fields
private readonly Func _f;
private bool _hasValue;
private T _value;
#endregion
#region Constructors
public MyLazy(Func f)
{
_f = f;
}
#endregion
#region Operators
//
// Use objects of type MyLazy as objects of type T
// through implicit keyword
//
public static implicit operator T(MyLazy lazy)
{
if (!lazy._hasValue)
{
lazy._value = lazy._f();
lazy._hasValue = true;
}
return lazy._value;
}
#endregion
}MyLazy是一个包含以下字段的泛型类:
- _f:延迟评估的函数,返回T类型值
- _value:T类型的值(冻结值)
- _hasValue:一个布尔值,指示是否已计算该值
为了使用类型MyLazy的对象作为类型T的对象,使用implicit关键字。评估在类型铸造时完成,此操作称为解冻。
因此,运行以下代码:
var myLazyRandom = new MyLazy(GetRandomNumber);
double myRandomX = myLazyRandom;
Console.WriteLine("\n Random with MyLazy: {0}", myRandomX);其中GetRandomNumber返回随机double如下:
static double GetRandomNumber()
{
Random r = new Random();
return r.NextDouble();
}给出以下输出:

.NET Framework 4引入了一个用于延迟评估的类System.Lazy。此类通过属性Value返回值。运行以下代码:
var lazyRandom = new Lazy(GetRandomNumber);
double randomX = lazyRandom;给出编译错误,因为类型Lazy与类型double不同。
要使用类System.Lazy的值,必须按如下方式使用该属性Value:
var lazyRandom = new Lazy(GetRandomNumber);
double randomX = lazyRandom.Value;
Console.WriteLine("\n Random with System.Lazy.Value: {0}", randomX);输出如下:

.NET Framework 4还为延迟评估推出了ThreadLocal和LazyInitializer。



