【正点原子STM32连载】第五十章 照相机实验 摘自【正点原子】MiniPro STM32H750 开发指南_V1.1

1）实验平台：正点原子MiniPro H750开发板 2）平台购买地址：https://detail.tmall.com/item.htm?id=677017430560 3）全套实验源码+手册+视频下载地址：http://www.openedv.com/thread-336836-1-1.html 4）对正点原子STM32感兴趣的同学可以加群讨论：879133275

第五十三章 DSP测试实验

上一章，我们测试了STM32H750的硬件FPU。STM32H750除了集成硬件FPU外，还支持多种DSP指令集。同时ST还提供了一整套DSP库方便我们工程中开发应用。 本章，我们将指导大家入门STM32H750的DSP，手把手教大家搭建DSP库测试环境，同时通过对DSP库中的几个基本数学功能函数和FFT快速傅里叶变换函数的测试，让大家对STM32H750的DSP库有个基本的了解。 本章分为如下几个小节： 53.1 DSP简介与环境搭建 53.2 硬件设计 53.3 程序设计 53.4 下载验证

53.1 DSP简介与环境搭建 本节将分两个部分：1，STM32H750 DSP简介；2，DSP库运行环境搭建。 53.1.1 STM32H750 DSP简介 STM32H750采用Cortex-M7内核，相比Cortex-M3系列除了内置硬件FPU单元，在数字信号处理方面还增加了DSP指令集，支持诸如单周期乘加指令（MAC），优化的单指令多数据指令（SIMD），饱和算数等多种数字信号处理指令集。相比Cortex-M3，Cortex-M7在数字信号处理能力方面得到了大大的提升。Cortex-M7执行所有的DSP指令集都可以在单周期内完成，而Cortex-M3需要多个指令和多个周期才能完成同样的功能。 接下来来介绍Cortex-M7的两个DSP指令：MAC指令（32位乘法累加）和SIMD指令。 32位乘法累加（MAC）单元包括新的指令集，能够在单周期内完成一个 32×32+ 64 64 的操作或两个16×16 的操作，其计算能力，如表53.1.1.1所示：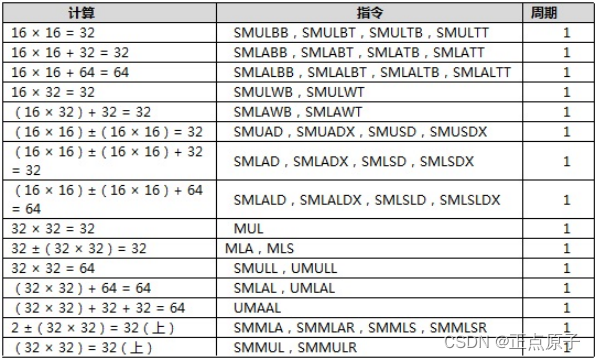

图53.1.1.1 32位乘法累加（MAC）单元的计算能力 Cortex-M7支持SIMD指令集，这在Cortex-M3/M0系列是不可用的。上述表中的指令，有的属于SIMD指令。与硬件乘法器一起工作（MAC），使所有这些指令都能在单个周期内执行。受益于SIMD指令的支持，Cortex-M4处理器能在单周期内完成高达32×32+6464的运算，为其他任务释放处理器的带宽，而不是被乘法和加法消耗运算资源。 比如一个比较复杂的运算：两个16×16乘法加上一个32位加法，如图53.1.1.2所示：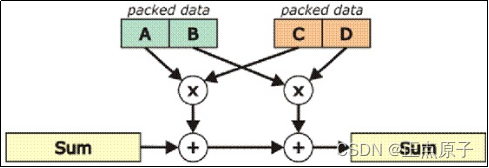

图53.1.1.2 SUM运算过程 以上图片所示的运算，即：SUM = SUM +（A* C）+（B *D），在STM32H750上面，可以被编译成由一条单周期指令完成。 上面我们简单的介绍了Cortex-M7的DSP指令，接下来我们来介绍一下STM32H7的DSP库。STM32H7的DSP库源码和测试实例在ST提供的HAL库：en.stm32cubeh7.zip里面就有（该文件可以在www.st.com网站下载，搜索STM32CubeH7即可找到最新版本），该文件在：光盘 8，STM32参考资料1，STM32CubeH7固件包文件夹里面，解压该文件，即可找到ST提供的DSP库，详细路径为：光盘8，STM32参考资料 1，STM32CubeH7固件包 STM32Cube_FW_H7_V1.6.0 DriversCMSISDSP，该文件夹下目录结构如图53.1.1.3所示：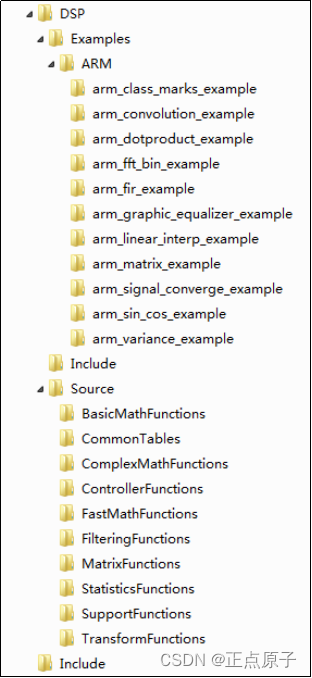

图53.1.1.3 DSP目录结构 DSP源码包的Source文件夹是所有DSP库的源码，Examples文件夹是相对应的一些测试实例。这些测试实例都是带main函数的，也就是拿到工程中可以直接使用。接下来我们一一讲解一下Source源码文件夹下面的子文件夹包含的DSP库的功能。 BasicMathFunctions 基本数学函数：提供浮点数的各种基本运算函数，如向量加减乘除等运算。 CommonTables arm_common_tables.c文件提供位翻转或相关参数表。arm_const_structs.c文件提供一些常用的常量结构体，方便用户使用。 ComplexMathFunctions 复数学功能，如向量处理，求模运算。 ControllerFunctions 控制功能函数。包括正弦余弦，PID电机控制，矢量Clarke变换，矢量Clarke逆变换。 FastMathFunctions 快速数学功能函数。提供了一种快速的近似正弦，余弦和平方根等相比CMSIS计算库要快的数学函数。 FilteringFunctions 滤波函数功能，主要为FIR和LMS（最小均方根）等滤波函数。 MatrixFunctions 矩阵处理函数。包括矩阵加法、矩阵初始化、矩阵反、矩阵乘法、矩阵规模、矩阵减法、矩阵转置等函数。 StatisticsFunctions 统计功能函数。如求平均值、最大值、最小值、计算均方根RMS、计算方差/标准差等。 SupportFunctions 支持功能函数，如数据拷贝，Q格式和浮点格式相互转换，Q任意格式相互转换。 TransformFunctions 变换功能。包括复数FFT（CFFT）/复数FFT逆运算（CIFFT）、实数FFT（RFFT）/实数FFT逆运算（RIFFT）、和DCT（离散余弦变换）和配套的初始化函数。 所有这些DSP库代码合在一起是比较多的，因此，ST为我们提了.lib格式的文件，方便使用。这些.lib文件就是由Source文件夹下的源码编译生成的，如果想看某个函数的源码，大家可以在Source文件夹下面查找。.lib格式文件HAL库包路径：DriversCMSISLibARM，针对M7的总共有6个.lib文件，如下： ① arm_cortexM7b_math.lib (Cortex-M7大端模式) ② arm_cortexM7l_math.lib (Cortex-M7小端模式) ③ arm_cortexM7bfdp_math.lib (双精度浮点Cortex-M7大端模式) ④arm_cortexM7lfdp_math.lib (双精度浮点Cortex-M7小端模式) ⑤arm_cortexM7bfsp_math.lib (单精度浮点Cortex-M7大端模式) ⑥arm_cortexM7lfsp_math.lib (单精度浮点Cortex-M7小端模式) 我们得根据所用MCU内核类型以及端模式来选择符合要求的.lib文件，本章我们所用的STM32H7属于CortexM7F内核，双精度浮点小端模式，应选择： arm_cortexM7lfdp_math.lib (双精度浮点Cortex-M7小端模式)。 对于DSP的子文件夹Examples下面存放的文件，是ST官方提供的一些DSP测试代码，提供简短的测试程序，方便上手，有兴趣的朋友可以根据需要自行测试。 53.1.2 DSP库运行环境搭建 本节我们将讲解怎么搭建DSP库运行环境，只要运行环境搭建好了，使用DSP库里面的函数来做相关处理就非常简单了。本节，我们将以上一章例程（实验40_1）为基础，搭建DSP运行环境。 在MDK里面搭建STM32H750的DSP运行环境(使用.lib方式)是很简单的，分为3个步骤： 1、添加文件。 首先，我们在实验41_1 DSP BasicMath测试实验\Drivers\CMSIS目录下新建：DSP和Lib文件夹，然后把官方的相应文件拉到我们的工程的相应位置：arm_cortexM7lfdp_math.lib和相关头文件，再把没用到的文件删除，如图53.1.2.1和图53.1.2.2所示：

图53.1.2.1 DSP_LIB文件夹添加文件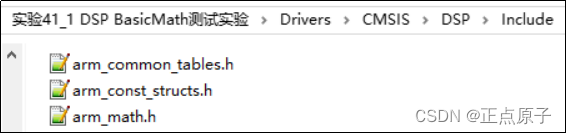

图53.1.2.2 DSP_LIB文件夹添加文件 这个步骤具体请参考工程源码文件，arm_cortexM7lfdp_math.lib文件在53.1.1节已经介绍过了。Include文件夹里面包含了我们可能要用到的相关头文件，所以要添加到工程中。 然后，打开工程，新建Drivers/CMSIS分组，并将arm_cortexM7lfdp_math.lib添加到工程里面，如图53.1.2.3所示：

图53.1.2.3 添加.lib文件 这样，添加文件就结束了（就添加了一个.lib文件）。 2、添加头文件包含路径 添加好.lib文件后，我们要添加头文件包含路径，这个我们工程都统一添加好了，所以不用额外再操作，这里是提醒一下大家要添加头文件包含路径，如图53.1.2.4所示：

图53.1.2.4 添加相关头文件包含路径 3、添加全局宏定义 最后，为了使用DSP库的所有功能，我们还需要添加几个全局宏定义： 1，__FPU_USED 2，__FPU_PRESENT 3，ARM_MATH_CM7 4，__CC_ARM 5，ARM_MATH_MATRIX_CHECK 6，ARM_MATH_ROUNDING 添加方法：点击C/C++选项卡，然后在Define里面进行设置，如图53.1.2.5所示：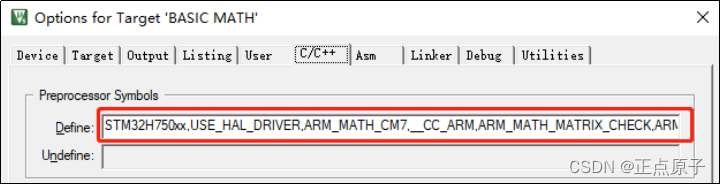

图53.1.2.5 DSP库支持全局宏定义设置 这里，两个宏之间用“,”隔开。并且，上面的全局宏里面，我们没有添加__FPU_USED和__FPU_PRESENT，因为在Target选项卡设置Floating Point Hardware的时候（上一章有介绍），只要我们选择了：Double Precision（如果没有设置Double Precision，则必须设置），MDK就会自动添加这两个全局宏，因此不需要我们手动添加了。这样，在Define处要输入的所有宏为：STM32H750xx,USE_HAL_DRIVER,ARM_MATH_CM7,__CC_ARM,ARM_MATH_MATRIX_CHECK,ARM_MATH_ROUNDING等共6个。 至此，STM32H750的DSP库运行环境就搭建完成了。 特别注意，为了方便调试，本章例程我们将MDK的优化设置为-O0优化，以得到最好的调试效果。 53.2 硬件设计

1. 例程功能 本例程包含2个源码：实验41_1 DSP BasicMath测试实验和实验41_2 DSP FFT测试实验，他们除了main.c里面内容不一样外，其他源码完全一模一样（包括MDK配置）。 实验41_1 DSP BasicMath测试实验功能简介：测试STM32H750的DSP库基础数学函数：arm_cos_f32和arm_sin_f32和标准库基础数学函数：cosf和sinf的速度差别，并在LCD屏幕上面显示两者计算所用时间。LED0闪烁，提示程序运行。 实验41_2 DSP FFT测试实验功能简介：测试STM32H750的DSP 库的FFT函数，程序运行后，自动生成1024点测试序列，然后，每当KEY0按下后，调用DSP库的FFT算法（基4法）执行FFT运算，在LCD屏幕上面显示运算时间，同时将FFT结果输出到串口。LED0闪烁，提示程序运行。
2. 硬件资源 1）RGB灯 RED ：LED0 - PB4 2）串口1(PA9/PA10连接在板载USB转串口芯片CH340上面) 3）正点原子2.8/3.5/4.3/7/10寸TFTLCD模块(仅限MCU屏，16位8080并口驱动) 4）独立按键 ：KEY0 - PA1 5）FPU(浮点计算单元) 6）定时器6 53.3 程序设计 本章代码，分成两个工程：1，实验52_1 DSP BasicMath测试；2，实验52_2 DSP FFT测试，接下来我们分别介绍。 53.3.1 DSP BasicMath测试 这是我们使用STM32H750的DSP库进行基础数学函数测试的一个例程。使用大家耳熟能详的公式进行计算： sin(x)2+cos(x)2=1 这里我们用到的就是sin和cos函数，不过实现方式不同。MDK的标准库（math.h）提供我们：sin、cos、sinf和cosf等4个函数，带f的表示单精度浮点型运算，即float型，而不带f的表示双精度浮点型，即double。 STM32H750的DSP库，则提供我们另外两个函数：arm_sin_f32和arm_cos_f32（注意：需要添加：arm_math.h头文件才可使用），这两个函数也是单精度浮点型的，用法同sinf和cosf一模一样。 本例程就是测试：arm_sin_f32& arm_cos_f32 同sinf&cosf的速度差别。 因为53.1.2节已经搭建好DSP库运行环境了，所以我们这里直接只需要修改main.c里面的代码即可，main.c代码如下：

#define DELTA   0.0001f         /* 误差值 */

/**
 * @brief       sin cos 测试
 * @param       angle : 起始角度
 * @param       times : 运算次数
 * @param       mode  : 是否使用DSP库
 *   @arg       0 , 不使用DSP库;
 *   @arg       1 , 使用DSP库;
 *
 * @retval      无
 */
uint8_t sin_cos_test(float angle, uint32_t times, uint8_t mode)
{
    float sinx, cosx;
    float result;
    uint32_t i = 0;
    if (mode == 0)
    {
        for (i = 0; i  DELTA)return 0XFF;      	/* 判断失败 */
            angle += 0.001f;    					/* 角度自增 */
        }
    }
    else
    {
        for (i = 0; i  DELTA)return 0XFF;      	/* 判断失败 */
            angle += 0.001f;    					/* 角度自增 */
        }
    }
    return 0;   /* 任务完成 */
}

uint8_t g_timeout;

int main(void)
{
    float time;
    char buf[50];
    uint8_t res;

    sys_cache_enable();                    	/* 打开L1-Cache */
    HAL_Init();                              	/* 初始化HAL库 */
    sys_stm32_clock_init(240, 2, 2, 4); 	/* 设置时钟, 480Mhz */
    delay_init(480);                        	/* 延时初始化 */
    usart_init(115200);                    	/* 串口初始化为115200 */
    mpu_memory_protection();              	/* 保护相关存储区域 */
    led_init();                              	/* 初始化LED */
    lcd_init();                              	/* 初始化LCD */
    btim_timx_int_init(65535, 24000 - 1);   /* 10Khz计数频率,最大计时6.5秒超出 */

    lcd_show_string(30, 50, 200, 16, 16, "STM32", RED);
    lcd_show_string(30, 70, 200, 16, 16, "DSP BasicMath TEST", RED);
    lcd_show_string(30, 90, 200, 16, 16, "ATOM@ALIENTEK", RED);
    lcd_show_string(30, 120, 200, 16, 16, "No DSP runtime:", RED);/*显示提示信息*/
    lcd_show_string(30, 150, 200, 16, 16, "Use DSP runtime:", RED);
    while (1)
    {
        /* 不使用DSP优化 */
        BTIM_TIMX_INT->CNT = 0; /* 重设TIM3定时器的计数器值 */
        g_timeout = 0;
        res = sin_cos_test(PI / 6, 1000000, 0);
        time = BTIM_TIMX_INT->CNT + (uint32_t)g_timeout * 65536;
        sprintf(buf, "%0.1fms\r\n", time / 10);

        if (res == 0)
        {
/* 显示运行时间 */
            lcd_show_string(30 + 16 * 8, 120, 100, 16, 16, buf, BLUE);      
        }
        else
        {
/* 显示当前运行情况 */
            lcd_show_string(30 + 16 * 8, 120, 100, 16, 16, "error！", BLUE); 
        }
        /* 使用DSP优化 */
        BTIM_TIMX_INT->CNT = 0; /* 重设TIM3定时器的计数器值 */
        g_timeout = 0;
        res = sin_cos_test(PI / 6, 1000000, 1);
        time = BTIM_TIMX_INT->CNT + (uint32_t)g_timeout * 65536;
        sprintf(buf, "%0.1fms\r\n", time / 10);
        if (res == 0)
        {
/* 显示运行时间 */
            lcd_show_string(30 + 16 * 8, 150, 100, 16, 16, buf, BLUE);      
        }
        else
        {
/* 显示错误 */
            lcd_show_string(30 + 16 * 8, 150, 100, 16, 16, "error！", BLUE); 
        }
        LED0_TOGGLE();
    }
}

这里包括2个函数：sin_cos_test和main函数，sin_cos_test函数用于根据给定参数，执行sin(x)2+cos(x)2=1的计算。计算完后，计算结果同给定的误差值（DELTA）对比，如果不大于误差值，则认为计算成功，否则计算失败。该函数可以根据给定的模式参数(mode)来决定使用哪个基础数学函数执行运算，从而得出对比。 main函数则比较简单，这里我们通过定时器3来统计sin_cos_test运行时间，从而得出对比数据。主循环里面，每次循环都会两次调用sin_cos_test函数，首先采用不使用DSP库方式计算，然后采用使用DSP库方式计算，并得出两次计算的时间，显示在LCD上面。 DSP基础数学函数测试的程序设计就讲解到这里。 53.3.2 DSP FFT测试 这是我们使用STM32H750的DSP库进行FFT函数测试的一个例程。 首先，我们简单介绍下FFT：FFT即快速傅里叶变换，可以将一个时域信号变换到频域。因为有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了，这就是很多信号分析采用FFT变换的原因。另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。简而言之，FFT就是将一个信号从时域变换到频域方便我们分析处理。 在实际应用中，一般的处理过程是先对一个信号在时域进行采集，比如我们通过ADC，按照一定大小采样频率F去采集信号，采集N个点，那么通过对这N个点进行FFT运算，就可以得到这个信号的频谱特性。 这里还涉及到一个采样定理的概念：在进行模拟/数字信号的转换过程中，当采样频率F大于信号中最高频率fmax的2倍时(F>2fmax)，采样之后的数字信号完整地保留了原始信号中的信息，采样定理又称奈奎斯特定理。举个简单的例子：比如我们正常人发声，频率范围一般在8KHz以内，那么我们要通过采样之后的数据来恢复声音，我们的采样频率必须为8KHz的2倍以上，也就是必须大于16KHz才行。 模拟信号经过ADC采样之后，就变成了数字信号，采样得到的数字信号，就可以做FFT变换了。N个采样点数据，在经过FFT之后，就可以得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。 假设采样频率为F，对一个信号采样，采样点数为N，那么FFT之后结果就是一个N点的复数，每一个点就对应着一个频率点（以基波频率为单位递增），这个点的模值（sqrt(实部2+虚部2)）就是该频点频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍，而第一个点就是直流分量，它的模值就是直流分量的N倍。 这里还有个基波频率，也叫频率分辨率的概念，就是如果我们按照F的采样频率去采集一个信号，一共采集N个点，那么基波频率（频率分辨率）就是fk=F/N。这样，第n个点对应信号频率为：F(n-1)/N；其中n≥1，当n=1时为直流分量。 关于FFT我们就介绍到这。 如果我们要自己实现FFT算法，对于不懂数字信号处理的朋友来说，是比较难的，不过，ST提供的STM32H750 DSP库里面就有FFT函数给我们调用，因此我们只需要知道如何使用这些函数，就可以迅速的完成FFT计算，而不需要自己学习数字信号处理，去编写代码了，大大方便了我们的开发。 STM32H750的DSP库里面，提供了定点和浮点 FFT实现方式，并且有基4的也有基2的，大家可以根据需要自由选择实现方式。注意：对于基4的FFT输入点数必须是4n，而基2的FFT输入点数则必须是2n，并且基4的FFT算法要比基2的快。 本章我们将采用DSP库里面的基4浮点FFT算法来实现FFT变换，并计算每个点的模值，所用到的函数有：

/* Deprecated */
arm_status arm_cfft_radix4_init_f32(arm_cfft_radix4_instance_f32 * S,
                    uint16_t fftLen,  uint8_t ifftFlag,  uint8_t bitReverseFlag);

/* Deprecated */
void arm_cfft_radix4_f32(const arm_cfft_radix4_instance_f32 * S,  
float32_t * pSrc);

/**
 * @brief  Floating-point complex magnitude
 * @param[in]  pSrc        points to the complex input vector
 * @param[out] pDst        points to the real output vector
 * @param[in]  numSamples  number of complex samples in the input vector
 */
void arm_cmplx_mag_f32(float32_t * pSrc, float32_t * pDst,uint32_t numSamples);

第一个函数arm_cfft_radix4_init_f32，用于初始化FFT运算相关参数，其中：fftLen用于指定FFT长度（16/64/256/1024/4096），本章设置为1024；ifftFlag用于指定是傅里叶变换(0)还是反傅里叶变换(1)，本章设置为0；bitReverseFlag用于设置是否按位取反，本章设置为1；最后，所有这些参数存储在一个arm_cfft_radix4_instance_f32结构体指针S里面。
第二个函数arm_cfft_radix4_f32就是执行基4浮点FFT运算的，pSrc传入采集到的输入信号数据（实部+虚部形式），同时FFT变换后的数据，也按顺序存放在pSrc里面，pSrc必须大于等于2倍fftLen长度。另外，S结构体指针参数是先由arm_cfft_radix4_init_f32函数设置好，然后传入该函数的。
第三个函数arm_cmplx_mag_f32用于计算复数模值，可以对FFT变换后的结果数据，执行取模操作。pSrc为复数输入数组（大小为2*numSamples）指针，指向FFT变换后的结果；pDst为输出数组（大小为numSamples）指针，存储取模后的值；numSamples就是总共有多少个数据需要取模。
通过这三个函数，我们便可以完成FFT计算，并取模值。本节例程（实验41_2 DSP FFT测试实验）同样是在53.1.2节已经搭建好DSP库运行环境上面修改代码，只需要修改main.c里面的代码即可，本例程main.c代码如下：   

/* FFT长度，默认是1024点FFT 
 * 可选范围为: 16, 64, 256, 1024.
 */
#define FFT_LENGTH      1024

float fft_inputbuf[FFT_LENGTH * 2];     /* FFT输入数组 */
float fft_outputbuf[FFT_LENGTH];        	/* FFT输出数组 */

uint8_t g_timeout;

int main(void)
{
    float time;
    char buf[50];
    arm_cfft_radix4_instance_f32 scfft;
    uint8_t key, t = 0;
    uint16_t i;

    sys_cache_enable();                    /* 打开L1-Cache */
    HAL_Init();                             	/* 初始化HAL库 */
    sys_stm32_clock_init(240, 2, 2, 4);	/* 设置时钟, 480Mhz */
    delay_init(480);                       	/* 延时初始化 */
    usart_init(115200);                   	/* 串口初始化为115200 */
    mpu_memory_protection();             	/* 保护相关存储区域 */
    led_init();                             	/* 初始化LED */
    lcd_init();                             	/* 初始化LCD */
    key_init();                             	/* 初始化按键 */
    btim_timx_int_init(65535, 24000 - 1);  /* 10Khz计数频率,最大计时6.5秒超出 */

    lcd_show_string(30, 50, 200, 16, 16, "STM32", RED);
    lcd_show_string(30, 70, 200, 16, 16, "DSP FFT TEST", RED);
    lcd_show_string(30, 90, 200, 16, 16, "ATOM@ALIENTEK", RED);
    lcd_show_string(30, 130, 200, 16, 16, "KEY0:Run FFT", RED); /* 显示提示信息 */
    lcd_show_string(30, 160, 200, 16, 16, "FFT runtime:", RED); /* 显示提示信息 */
/* 初始化scfft结构体，设定FFT相关参数 */
    arm_cfft_radix4_init_f32(&scfft, FFT_LENGTH, 0, 1); 

    while (1)
    {
        key = key_scan(0);
        if (key == KEY0_PRES)
        {
            for (i = 0; i CNT = 0;; /* 重设BTIM_TIMX_INT定时器的计数器值 */
            g_timeout = 0;
            
            arm_cfft_radix4_f32(&scfft, fft_inputbuf);      /* FFT计算（基4） */
            /* 计算所用时间 */
            time = BTIM_TIMX_INT->CNT + (uint32_t)g_timeout * 65536; 
            sprintf((char *)buf, "%0.3fms\r\n", time / 1000);
/* 显示运行时间 */
            lcd_show_string(30 + 12 * 8, 160, 100, 16, 16, buf, BLUE);      
            /* 把运算结果复数求模得幅值 */
            arm_cmplx_mag_f32(fft_inputbuf, fft_outputbuf, FFT_LENGTH);     
            
            printf("\r\n%d point FFT runtime:%0.3fms\r\n", FFT_LENGTH,
 time / 1000);
            printf("FFT Result:\r\n");

            for (i = 0; i