【数据结构与算法】线索化二叉树的介绍和程序实现

1. 为什么有线索化二叉树

二叉树的遍历是用递归来实现的，效率相对来说会低一些。为了提高遍历的效率，就有了线索化二叉树

2. 线索化二叉树的介绍

现在我们看线索化二叉树是如何提高遍历的效率的。先将数列{1, 3, 6, 8, 10, 14}构建成一颗二叉树，如下所示：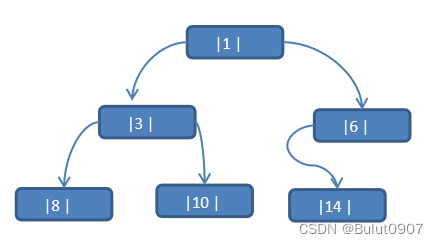

可以看到6, 8, 10, 14这几个节点的左右指针是空指针域，得出n个结点的二叉树中含有n+1【公式2n-(n-1)=n+1】个空指针域。以空间换时间的思想，将二叉树中的左空指针域，指向该节点前序/中序/后序遍历下的前一个节点(前驱节点)，将二叉树中的右空指针域，指向该节点前序/中序/后序遍历下的后一个节点(后继节点)。这种附加的指针称为线索，加上线索的二叉树称为线索化二叉树(Threaded BinaryTree)

所以一个节点的左右指针域可能指向的是左右子树，也可能指向的是前驱节点/后继节点

3. 中序线索化二叉树的程序实现

需求：将上面的二叉树，修改为中序线索化二叉树，然后进行遍历

中序线索化二叉树的实现思路： 上面的二叉树的中序遍历结果为：{8, 3, 10, 1, 14, 6}，则修改为中序线索化二叉树的结果如下：

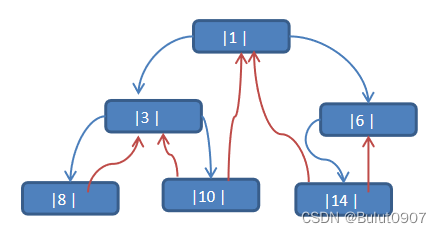遍历中序线索化二叉树思路：

因为线索化后，各个结点指向发生变化，无需使用递归方式进行遍历，各个节点可以通过线型方式遍历。提高了遍历的效率。遍历中序线索二叉树和遍历中序二叉树的结果一样

程序如下：

public class ThreadedBinaryTreeDemo {

    public static void main(String[] args) {
        // 创建一颗线索化二叉树
        ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();

        // // 创建需要的节点
        Node root = new Node(1, "node1");
        Node node2 = new Node(3, "node3");
        Node node3 = new Node(6, "node6");
        Node node4 = new Node(8, "node8");
        Node node5 = new Node(10, "node10");
        Node node6 = new Node(14, "node14");

        // 各个节点形成子树
        root.left = node2;
        root.right = node3;
        node2.left = node4;
        node2.right = node5;
        node3.left = node6;

        // 将root节点添加到线索化二叉树
        threadedBinaryTree.setRoot(root);

        // 对中序线索化二叉树的初始二叉树进行中序线索化
        threadedBinaryTree.infixThreaded();

        // 以id为10的node5进行测试
        Node leftNode = node5.left;
        Node rightNode = node5.right;
        System.out.println("id为10的node5节点的前驱结点是 = " + leftNode);
        System.out.println("id为10的node5节点的后继结点是 = " + rightNode);

        // 遍历线索化二叉树
        System.out.println("使用线索化的方式遍历中序线索化二叉树: ");
        threadedBinaryTree.infixThreadedShow();
    }

}


// 树的Node节点
class Node {
    public int id;
    public String name;
    // 默认为null
    public Node left;
    // 默认为null
    public Node right;
    // leftType等于0表示指向的是左子树, 等于1表示指向前驱节点
    // rightType等于0表示指向是右子树, 等于1表示指向后继节点
    public int leftType;
    public int rightType;

    public Node(int id, String name) {
        this.id = id;
        this.name = name;
    }

    @Override
    public String toString() {
        return "Node [id = " + id + ", name = " + name + "]";
    }


}


// ThreadedBinaryTree线索化二叉树
class ThreadedBinaryTree {
    private Node root;

    // 为了实现线索化，创建一个变量指向当前结点的前驱结点
    // 当前节点变化，preNode同步变化
    private Node preNode = null;

    public void setRoot(Node root) {
        this.root = root;
    }


    // 重载infixThreaded方法
    public void infixThreaded() {
        this.infixThreaded(root);
    }


    // 对二叉树进行中序线索化
    // 重点：其实就是进行一次二叉树的中序遍历，在这个过程中，
    //      对每个节点的左空指针域赋值为前驱节点，对每个节点的右空指针域赋值为后继节点
    public void infixThreaded(Node node) {
        // 如果node==null, 不能线索化
        if (node == null) {
            return;
        } else {
            // 先线索化左子树
            infixThreaded(node.left);


            // >>>>>>开始线索化当前结点>>>>>>
            // 如果当前节点的left为空指针域，则将左空指针域赋值为前驱节点
            // 对于中序遍历的第一个节点，前驱节点可能为null
            if (node.left == null) {
                node.left = preNode;
                node.leftType = 1;
            }

            // 重点：因为当前节点目前并不知道它的后继节点是哪个，所以只能递归到下一轮线索化时，
            //      通过preNode设置node

            // 如果preNode的right为空指针域，则将右空指针域赋值为后继节点
            // 对于中序遍历的最后一个节点，不会递归到下一轮线索化
            if (preNode != null && preNode.right == null) {
                preNode.right = node;
                preNode.rightType = 1;
            }
            // 将当前节点是下一个节点的前驱节点，便于后续的线索化
            preNode = node;
            // >>>>>>结束线索化当前结点>>>>>>

            // 线索化右子树
            infixThreaded(node.right);
        }


    }


    // 遍历中序线索化二叉树的方法
    public void infixThreadedShow() {
        Node currentNode = root;
        while (currentNode != null) {

            // 向左循环找到leftType == 1的结点，即线索化的节点
            while (currentNode.leftType == 0) {
                // 因为线索化二叉树的所有节点都有left，只有第一个线索化的节点left = null，但leftType = 1
                // 所以leftType == 0时, left不会为null
                currentNode = currentNode.left;
            }

            // 然后打印线索化的节点
            System.out.println(currentNode);

            // 如果后面的节点是线索化的节点，则循环输出
            while (currentNode.rightType == 1) {
                // 因为线索化二叉树除了最后一个节点，都有right, 但最后一个节点的right为null，rightType = 0
                // 所有当rightType == 1时, right不会为null
                currentNode = currentNode.right;
                System.out.println(currentNode);
            }
            // 如果后面的节点不是线索化的节点，而是右子树，则跳到右子树，循环处理
            currentNode = currentNode.right;
        }
    }


}

运行程序，结果如下：

id为10的node5节点的前驱结点是 = Node [id = 3, name = node3]
id为10的node5节点的后继结点是 = Node [id = 1, name = node1]
使用线索化的方式遍历中序线索化二叉树: 
Node [id = 8, name = node8]
Node [id = 3, name = node3]
Node [id = 10, name = node10]
Node [id = 1, name = node1]
Node [id = 14, name = node14]
Node [id = 6, name = node6]