【第六周：统计学】7周成为数据分析师

本课程共七个章节，课程地址：7周成为数据分析师（完结）_哔哩哔哩_bilibili

1. 数据分析思维
2. 业务知识
3. Excel
4. 数据可视化
5. SQL
6. 统计学
7. Python 

第六周：统计学（P77-P85） 

1. 描述统计学
2. 概率（推断统计学）

目录

第六周：统计学（P77-P85） 

一、描述统计学

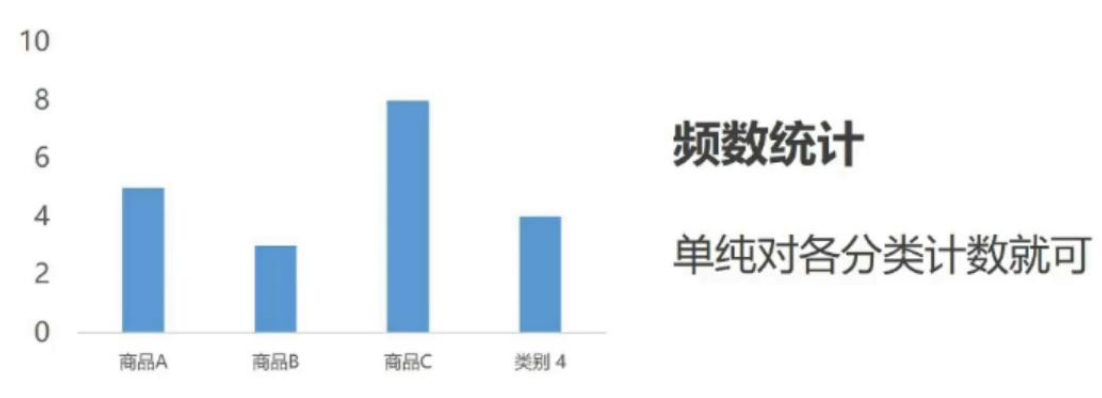
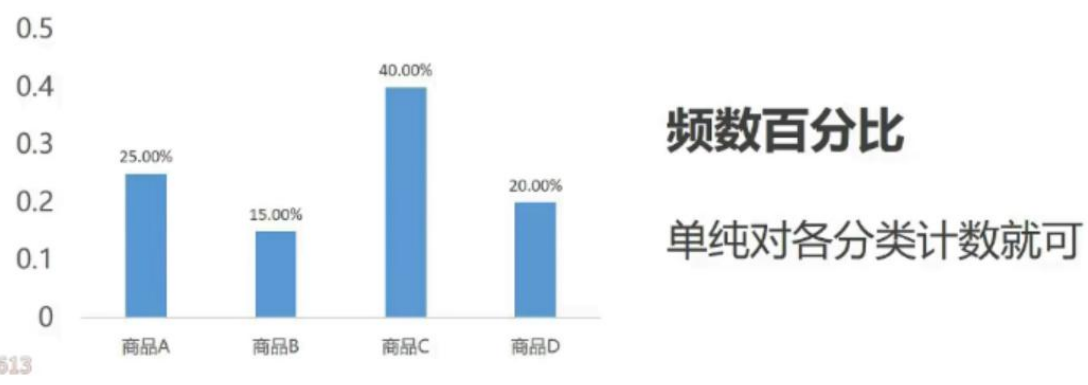
（一）分类数据描述统计

• 频数统计
• 频数百分比

（二）数值数据描述统计 

• 统计度量：平均数（AVERAGE()函数）、中位数（MEDIAN()函数）、众数（MODE()函数）、分位数（QUARTILE()函数）、方差（VAR.P()函数）、标准差（STDEV.P()函数）、数据标准化（Z-Score）、权重预估、切比雪夫定理
• 图形（可视化）：箱线图、直方图、偏度、直方图中的标准型分布/正态分布、切比雪夫定理V2.0

二、概率（推断统计学） 

（一）概率 

（二）贝叶斯定理  

一、描述统计学

• 针对业务分析和商业分析
• 描述和推断

一般把数据分为两类，两者是可以相互换算的：

• 数值数据：直接进行加减乘除运算的数据（int / float）
• 分类数据：类别、文本数据，不能进行数值运算

（一）分类数据描述统计

 

（二）数值数据描述统计 

1. 统计度量

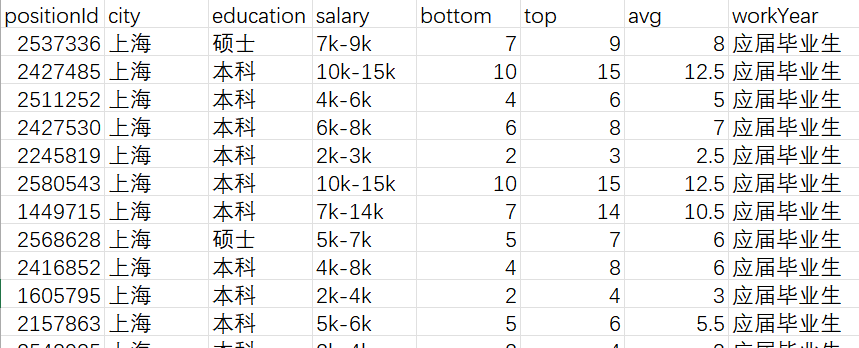
• 平均数（AVERAGE()函数）：数据分布不均匀时使用平均数是非常不靠谱的
• 中位数（MEDIAN()函数）：把一个数字从大到小进行排列，排在中间的数，或排在中间的两个数的平均数

当平均数>中位数时，说明数字不太均衡，且往较大值偏移；两者差的越多，说明数字越不均衡 

• 众数（MODE()函数）：出现频率最高的那个数字
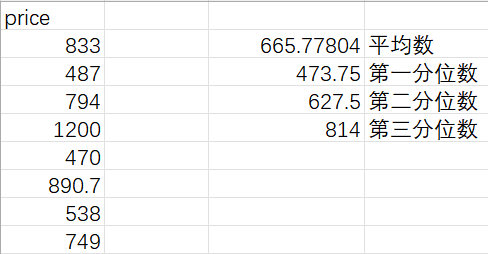
• 分位数（以四分位数为例，QUARTILE()函数）：将一组数据从小到大排列好，均匀地四等分

 

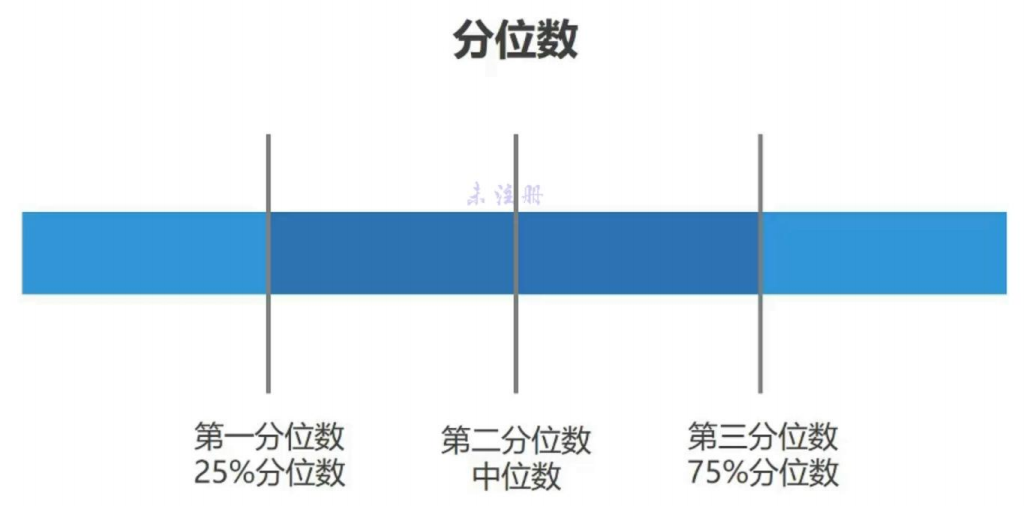
二八法则：可以跟分位数结合使用。对于20%的分位数来说，占了80%的贡献 

例：对用户消费按照四分位法来进行分析

由于数据量太大，只取20%

 

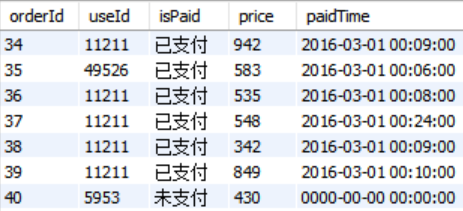
SELECT price FROM data.orderinfo
where right(useId,1) in (0,1)   # 从右截取useId一位，即取useId最右边数字为0或1的记录

导出为 test.csv

• 方差（VAR.P()函数）：描述数据的离散程度/波动性/稳定性。方差越大，波动性越强，数据也就越离散 

 

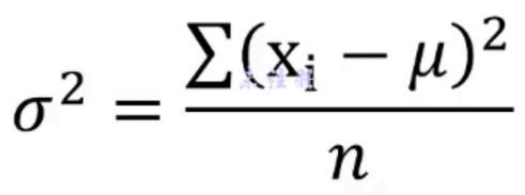
方差会抹消掉数据的单位，失去了业务的含义。故引入标准差，异常的单位也变得正常，跟业务更贴合，故更常用 

• 标准差（STDEV.P()函数）：对方差加个根号（SQRT()函数）

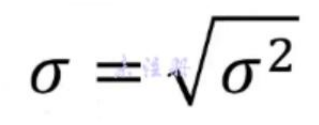
上下限：（平均值－标准差，平均值＋标准差）

注：大部分数据在该范围内波动，但不是囊括所有数据

• 数据标准化（Z-Score）：数据的量纲/单位不一致时。将两组不能直接对比的数据标准化后，数据能直接进行对比，趋势更加清晰明了

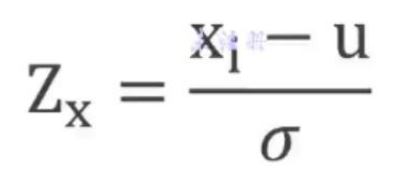
例：求出所有订单量，按日统计 

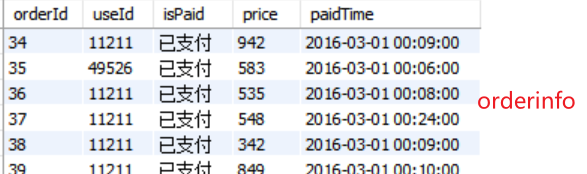
SELECT date(paidTime), count(orderId) FROM data.orderinfo
where paidTime > '0000-00-00'
group by date(paidTime)

把结果导出为 test1.csv，如下： 

 

 

 

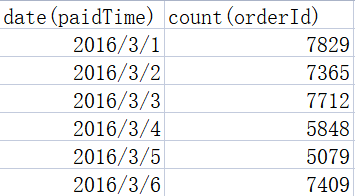
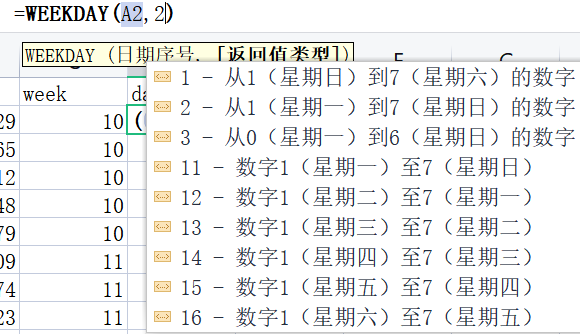
如下：

 

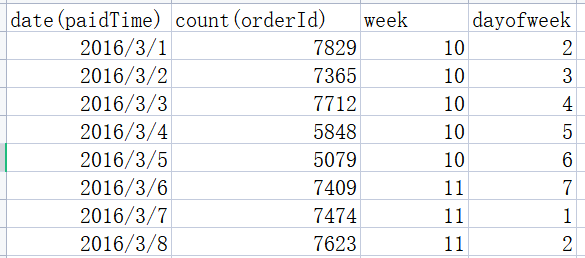
对其插入数据透视表：

• 行：week
• 列：dayofweek
• 值：求和项:count(orderId) 

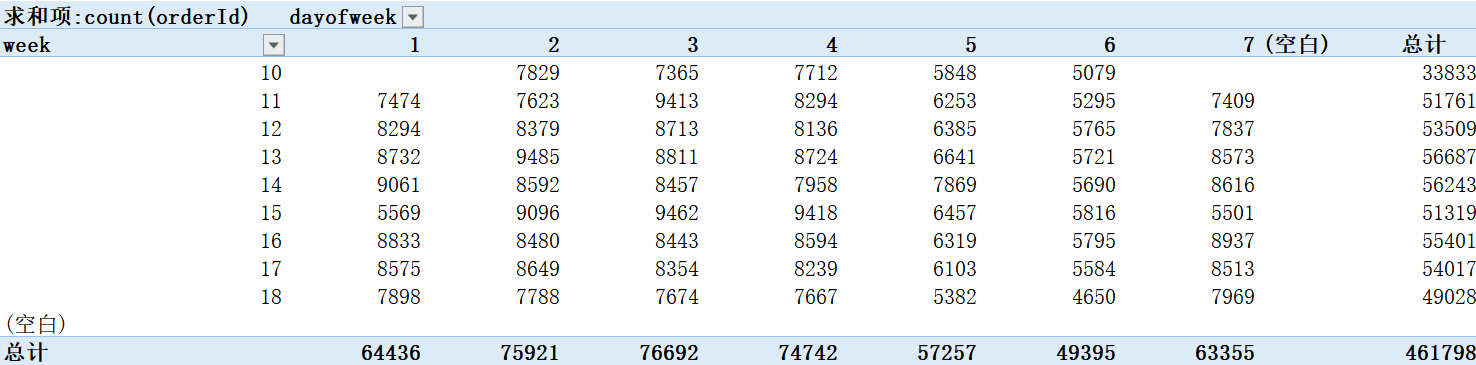
对上表进行标准化（标准化之后数据的可视化更加清晰明了）：

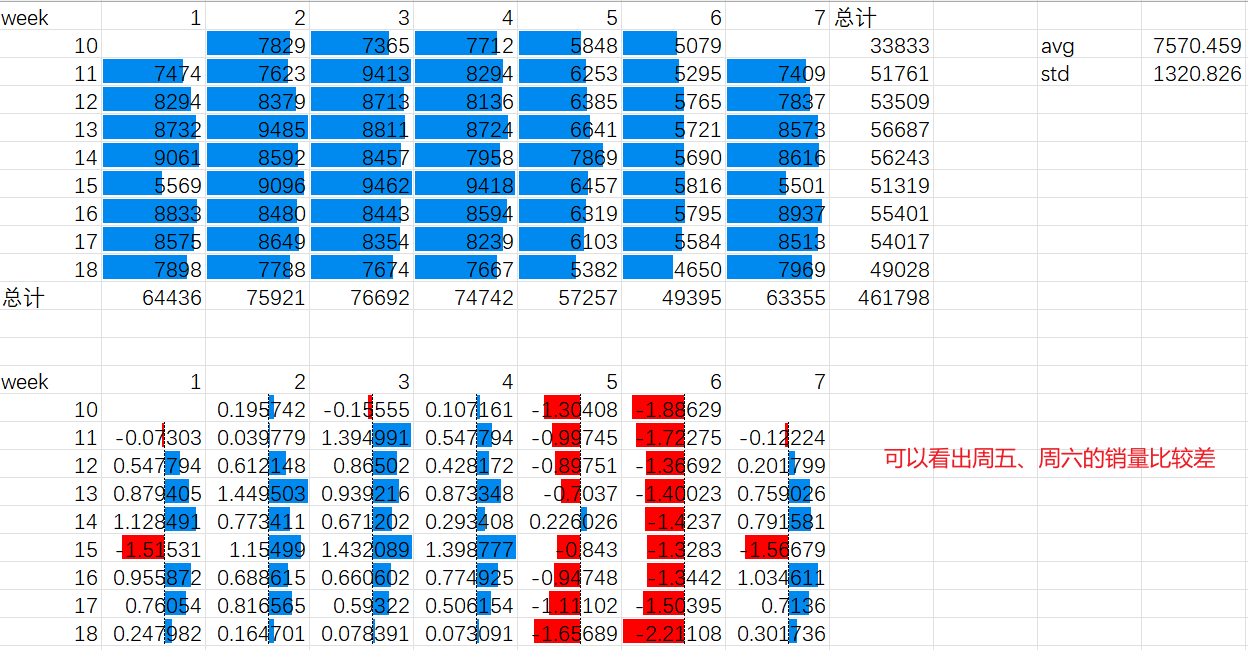
注：要使某个单元格的值在拖动的时候固定不变，要在该单元格前加$符号

如，单元格L3 ——> $L$3  

• 权重预估 

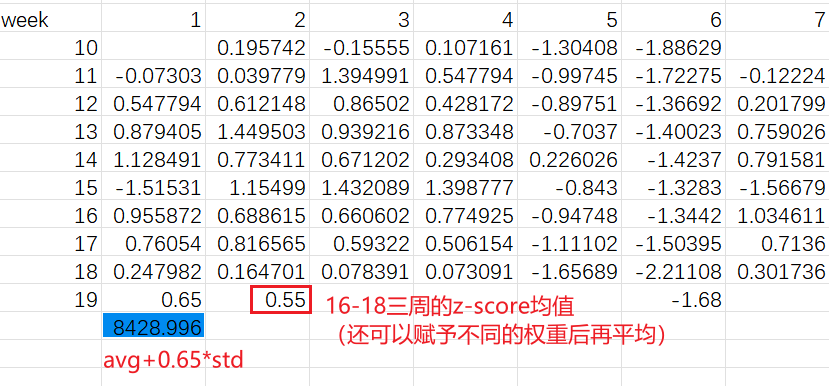
可以用16-18周的数据（可以直接均值，或每周分配不同权重后再求平均）来预估19周的数据（比平均值高出多少个标准差）

 

外卖订单销量 VS 温度：将两者都标准化后再对比分析（散点图等），比较容易较快看出规律

• 切比雪夫定理：确定数据范围、异常值检测

例：渠道推广

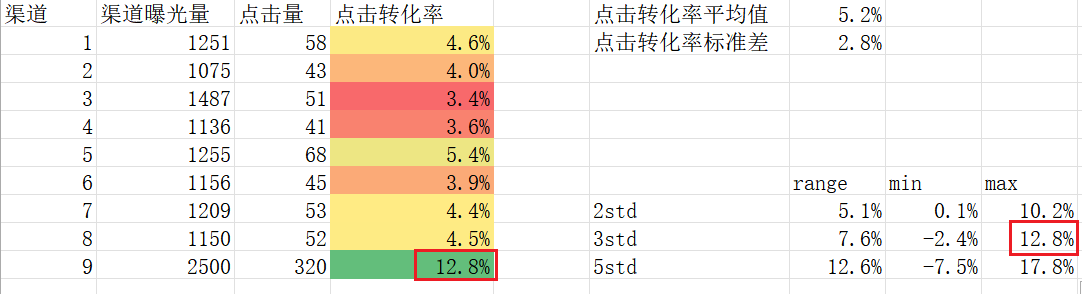
故该值（12.8%）不算极端异常值 

2. 图形（可视化）

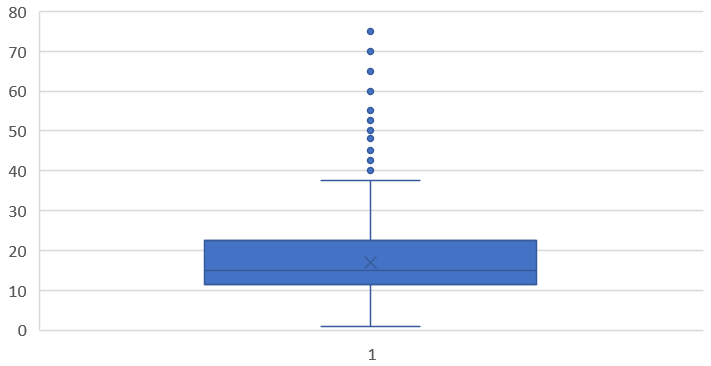
• 箱线图：与分位数息息相关，描述一组数据的分布

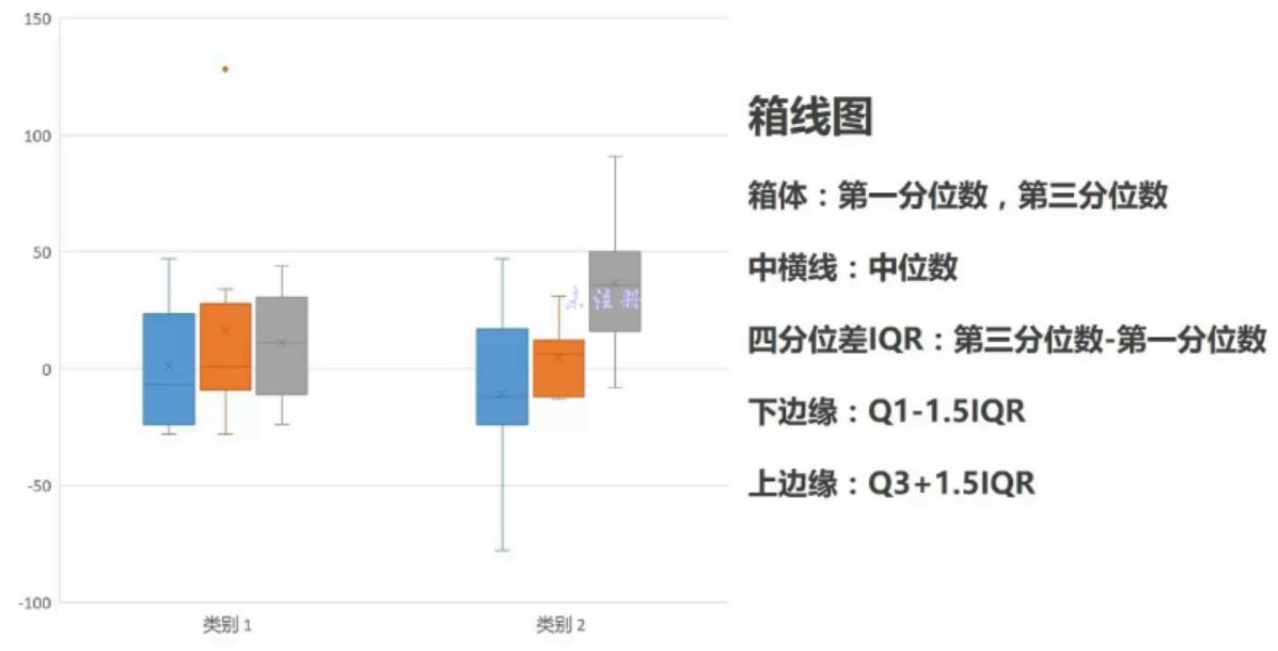
上下边缘可以用来估计异常值

在Excel中画箱线图：插入 - 推荐的图表 - 所有图表 - 箱形图

对avg列画箱线图：

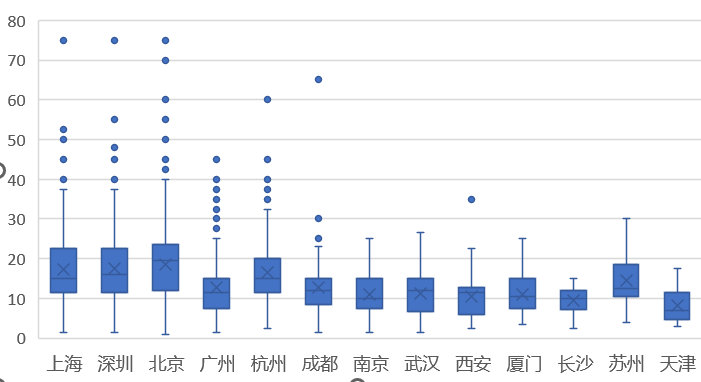
对avg列和city列画箱线图：

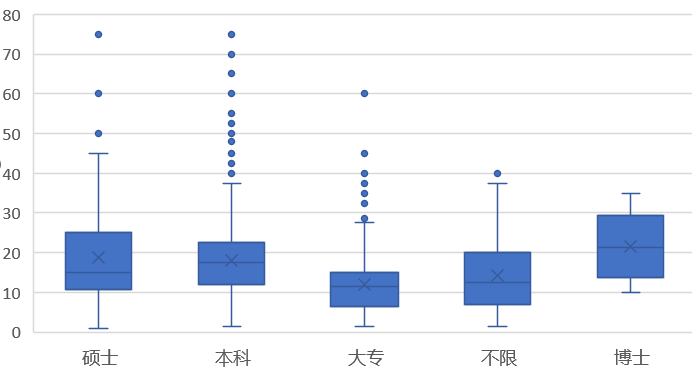
对avg列和education列画箱线图： 

 

• 直方图：特殊的柱形图，描述类别数据

 在Excel中画直方图：插入 - 直方图

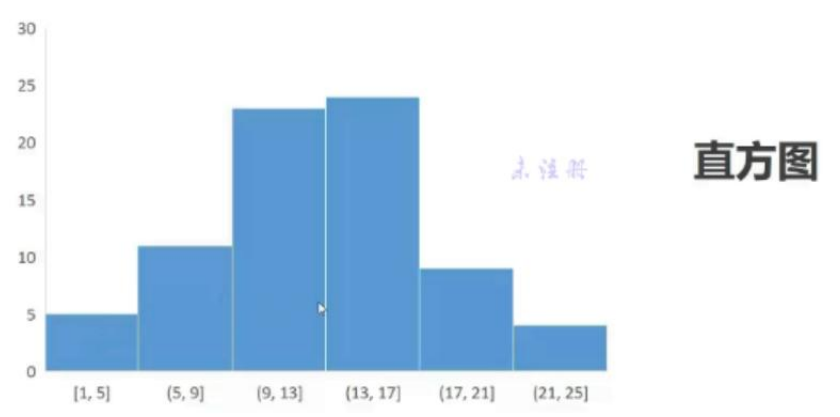
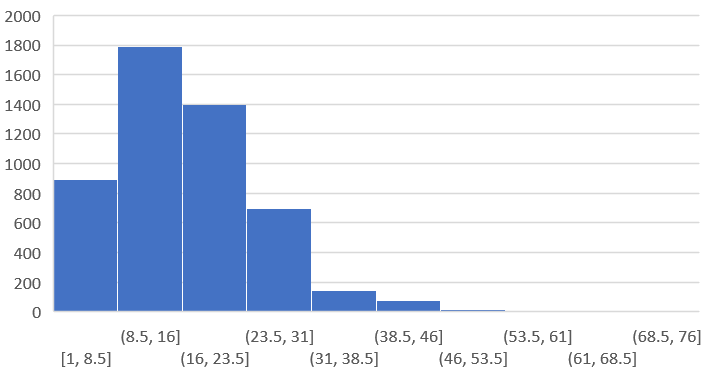
对avg列画直方图： 

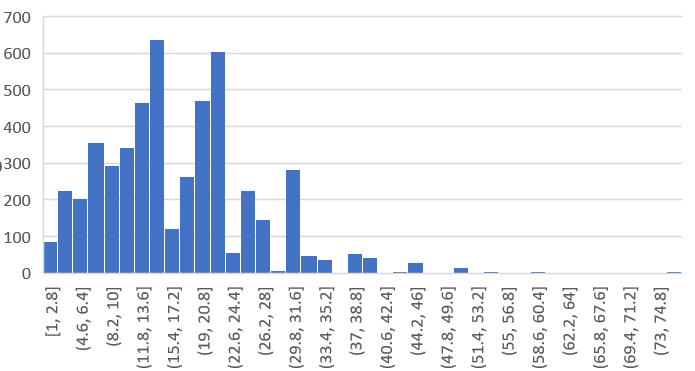
右键 - 设置坐标轴格式 - 箱宽度（设置为7.5） & 箱数（均匀地把数据进行几等分，设置为10） 

 

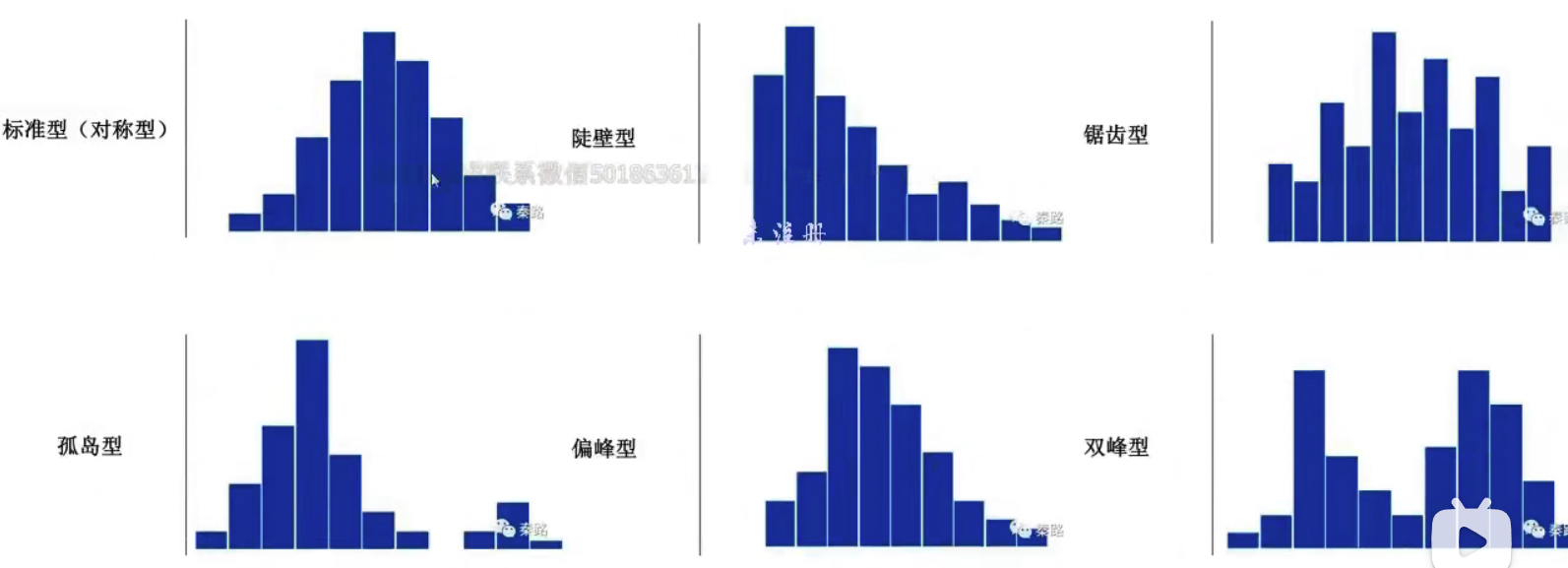
• 陡壁型：容易出现在消费领域
• 锯齿型：薪资数据，说明数据不够稳定，数据采集时有来源的偏差
• 孤岛型： 一批异常值
• 偏峰型：会有一边是长尾
• 双峰型：两个数据源混合

• 偏度：数据是往左偏（负值，长尾在左）还是往右偏（正值，长尾在右）

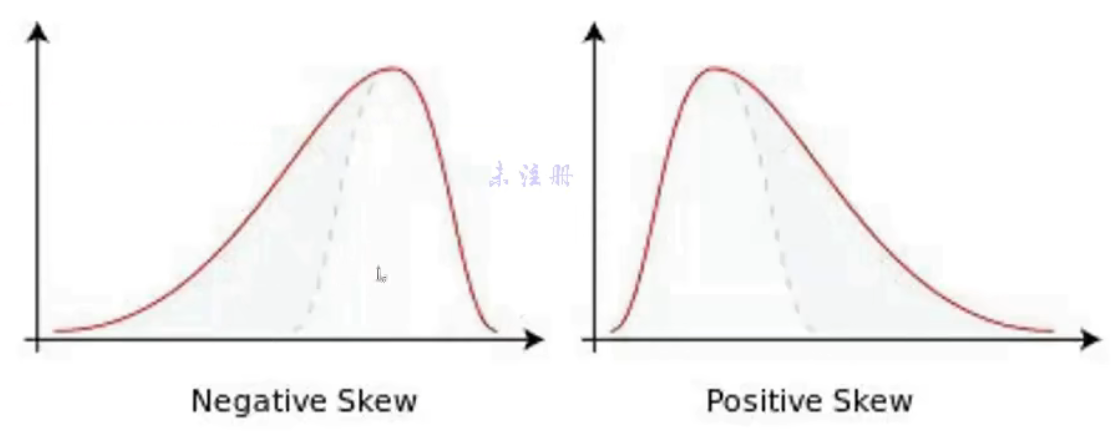
• 直方图中的标准型分布（正态分布）/ 切比雪夫定理V2.0 

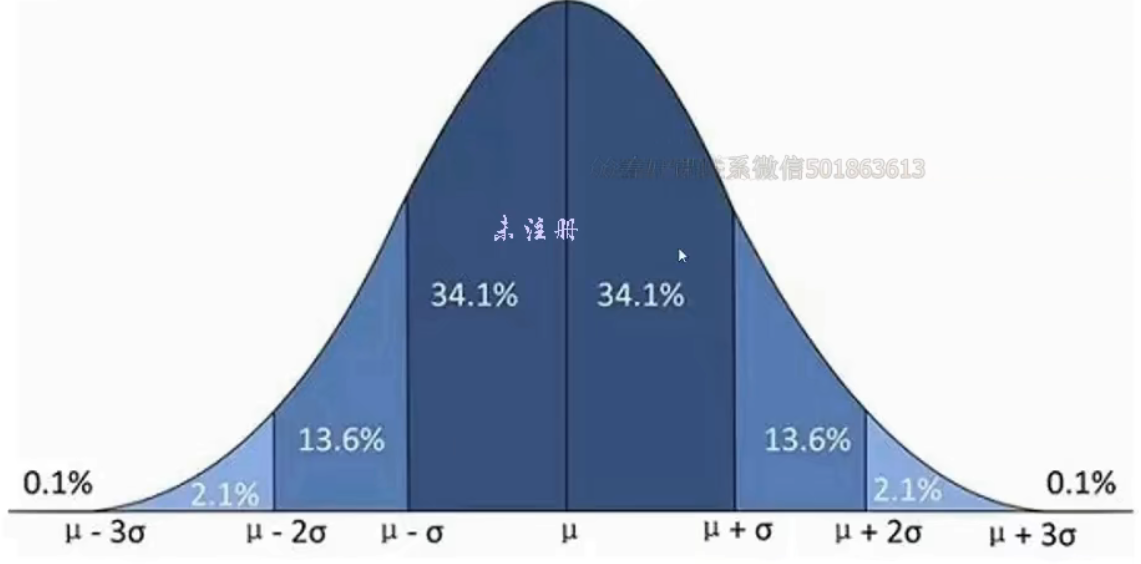
例：综合练习

数据 - 数据分析 - 描述统计

 

 

二、概率（推断统计学）  （一）概率 

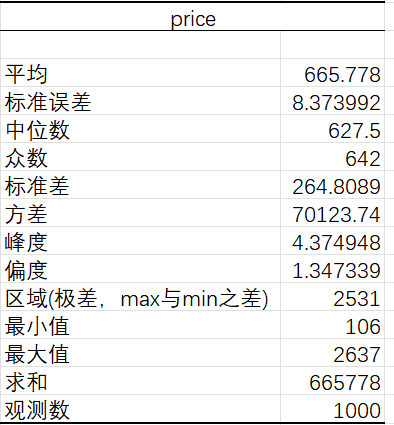
• 75%
• 25%
• 25%
• 75% 

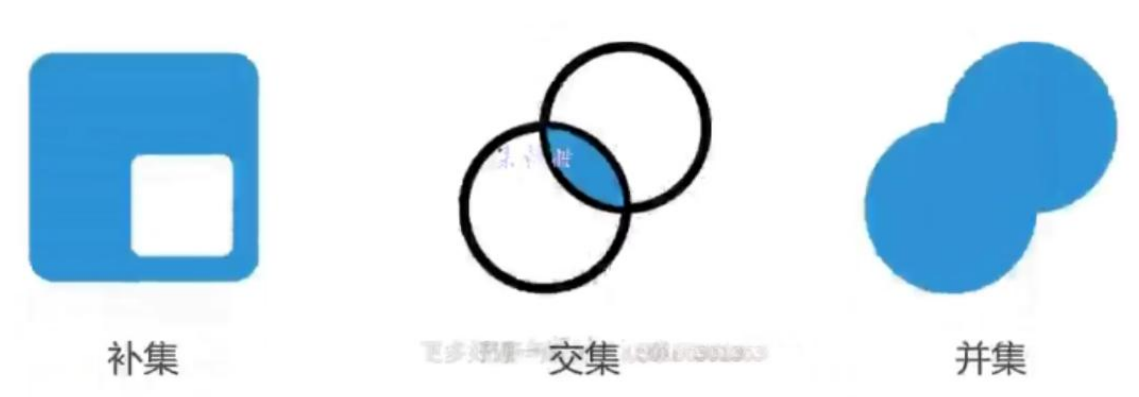
• 事件A的补集：所有不属于事件A的样本组成的事件，A的补集 = 1 - A
• 交集（SQL里的inner join）：既属于A，又属于B 
• 并集（或者）

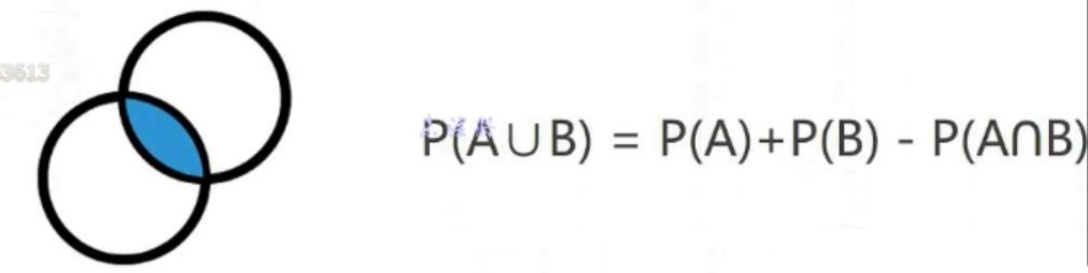
• 条件概率：在某个已知条件发生的情况下， 考虑一个事件发生的可能性
• 独立事件

（二）贝叶斯定理 

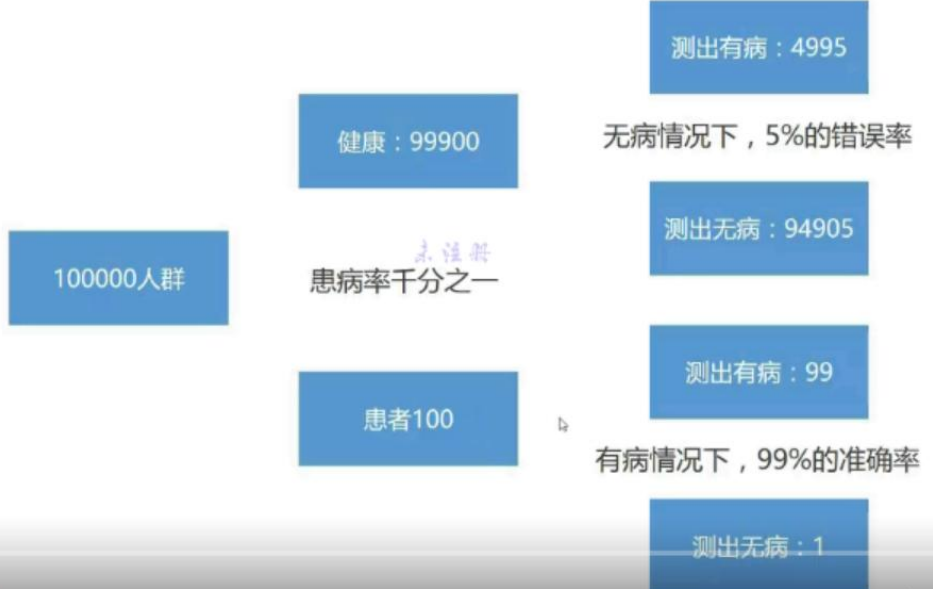
• 真的得病：99
• 试纸说一个患者得病：4995+99 = 5094
• 概率：99/5094 = 0.019 = 1.9%

 

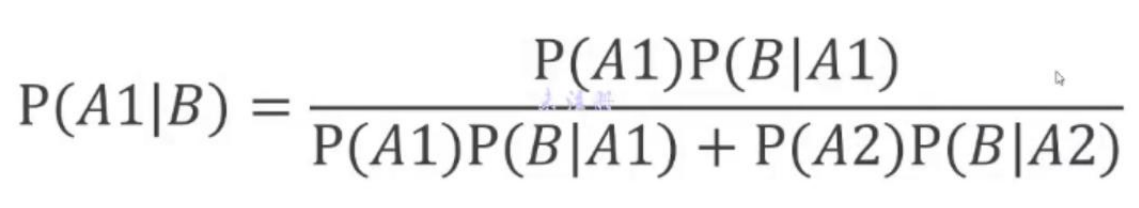
贝叶斯定理通用公式（知道结果A已经发生了，想要反过来推导结果发生的原因造成的可能性有多大）：

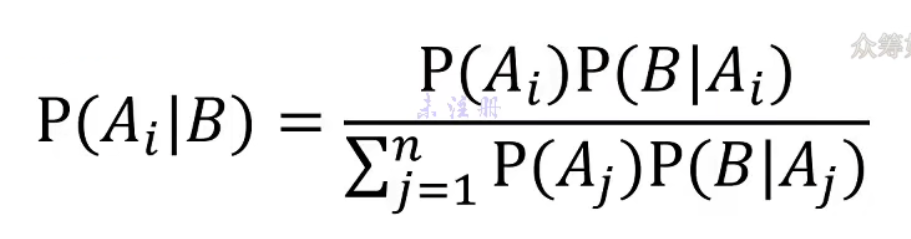
例1：

• 不能说明，女性只有30%是一个结果
• 一开始推广的目标人群中女性的比例有多少？（先验条件） 
• 不能通过结果判定结果，而是要通过结果反推原因发生的可能性 

例2：

0.8*0.15 / (0.8*0.15 + 0.2*0.85) = 41.38%

贝叶斯公式和全概率公式的关系 - 知乎 

例3：

• 1000条正常短信中，包含澳门赌场的短信有2条：2/1000 = 0.2%
• 1000条垃圾短信中，包含澳门赌场的短信有400条：400/1000 = 40%
• P(垃圾短信 | 包含澳门赌场) = P(既是垃圾短信又包含澳门赌场) / P(包含澳门赌场) = 50%*40% / (50%*40% + 50%*0.2%) = 99.5%

数据分析--统计分析和概率相关 - 知乎

06概率的世界 - 知乎

模型：朴素贝叶斯