贤鱼的刷题日常---【c++图论】洛谷 P3366最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 N,MN,M，表示该图共有 NN 个结点和 MM 条无向边。

接下来 MM 行每行包含三个整数 X_i,Y_i,Z_iXi​,Yi​,Zi​，表示有一条长度为 Z_iZi​ 的无向边连接结点 X_i,Y_iXi​,Yi​。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

输入输出样例

输入 #1复制

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出 #1复制

7

说明/提示

数据规模：

对于 20\%20% 的数据，N\le 5N≤5，M\le 20M≤20。

对于 40\%40% 的数据，N\le 50N≤50，M\le 2500M≤2500。

对于 70\%70% 的数据，N\le 500N≤500，M\le 10^4M≤104。

对于 100\%100% 的数据：1\le N\le 50001≤N≤5000，1\le M\le 2\times 10^51≤M≤2×105，1\le Z_i \le 10^41≤Zi​≤104。

样例解释：

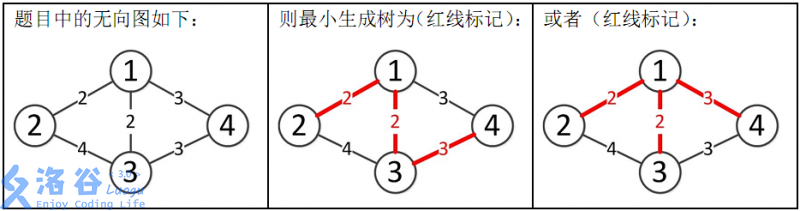
所以最小生成树的总边权为 2+2+3=72+2+3=7。

 具体做法：（如有问题可以私信，还请各位多多包含）

#include
#include
#include
#include
#include
using namespace std;
struct node{
	int u,v,w,next;

	bool operator < (const node &a)const{
		return wn>>m;
	for(int i=1;ie[i].u>>e[i].v>>e[i].w;
/*
这里建议单独开一个函数；
将输入改成int a,b,c;
cin>>a>>b>>c;
addedge(a,b,c);
在上方写一个函数(此题暂时不需要e[].next)
开始加边；
int ecnt=0;记录边数
void addedge(int u,int v,int w){
       e[++ecnt].u=u;
        e[ecnt].v=v;
        e[ecnt].w=w;
}
*/
	}
	int x=kruskal();
	if(x==-1) 
		cout