Householder矩阵定义如下：
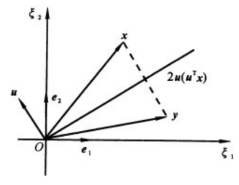
Q = I − 2 u u T (1) Q=I-2 uu^T\tag{1} Q=I−2uuT(1) 其中 u \mathbf{u} u为单位向量。对某一向量左乘 Q Q Q即对其进行Householder变换。其具体物理意义如下图所示：
Q
x
=
x
−
2
u
u
T
x
=
y
Qx = x - 2uu^T\mathbf{x}=\mathbf{y}
Qx=x−2uuTx=y 也即，该Householder变换就是对
x
x
x进行了镜面反射，该镜面与
u
\mathbf{u}
u垂直。
那么，如果想将任意向量 x x x变换到方向 e 1 = [ 1 0 ⋯ 0 ] e_1=\left[\begin{array}{llll}1 & 0 & \cdots & 0\end{array}\right] e1=[10⋯0]上，就可以通过Householder变换实现。 如下图所示：
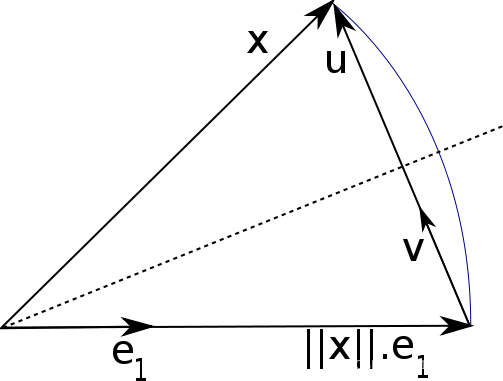由于是镜面反射，因此虚线势必是角平分线，且与
u
\mathbf{u}
u垂直，因此这是个等腰三角形。 故镜面反射后得到的结果应该为
∥
x
∥
e
1
\|x\|{e}_1
∥x∥e1，因此，有：
u
=
x
−
α
e
1
v
=
u
∥
u
∥
Q
=
I
−
2
v
v
⊤
\begin{aligned} &\mathbf{u}=\mathbf{x}-\alpha \mathbf{e}_{1} \\ &\mathbf{v}=\frac{\mathbf{u}}{\|\mathbf{u}\|} \\ &Q=I-2 \mathbf{v} \mathbf{v}^{\top} \end{aligned}
u=x−αe1v=∥u∥uQ=I−2vv⊤
注意到，很容易验证， Householder matrix是一个酉阵，且共轭对称。利用这一变换，我们可以实现对 A A A矩阵的QR分解。 首先，对于 A A A的第一列 a 1 a_1 a1，我们可以找到 Q 1 Q_1 Q1，满足： Q 1 a 1 = [ α 1 0 ⋮ 0 ] Q_1 a_1=\left[\begin{array}{c} \alpha_1 \\ 0 \\ \vdots \\ 0 \end{array}\right] Q1a1=⎣⎢⎢⎢⎡α10⋮0⎦⎥⎥⎥⎤ 即通过Householder变换到 e 1 e_1 e1方向上。此时， Q 1 A Q_1A Q1A可写为： Q 1 A = [ α 1 ⋆ ⋯ ⋆ 0 ⋮ A ′ 0 ] Q_{1} A=\left[\begin{array}{cccc} \alpha_{1} & \star & \cdots & \star \\ 0 & & & \\ \vdots & & & A^{\prime} \\ 0 & & & \end{array}\right] Q1A=⎣⎢⎢⎢⎡α10⋮0⋆⋯⋆A′⎦⎥⎥⎥⎤ 也即我们将第一列中除了第一行元素外的所有元素变为了0. 我们的目的是将矩阵 A A A变换为一个上三角矩阵。因此，接下来不用再管第一行，只需对右下角矩阵进行类似变换， 即对于矩阵 A ′ A^{\prime} A′，也可以找到一个对应的矩阵 Q 2 ′ Q_2^\prime Q2′使得 Q 2 ′ A ′ Q_2^\prime A^{\prime} Q2′A′的第一列除了第一个元素外的全部元素归0.为使得维度一致，我们可以定义： Q k = [ I k − 1 0 0 Q k ′ ] Q_{k}=\left[\begin{array}{cc} I_{k-1} & 0 \\ 0 & Q_{k}^{\prime} \end{array}\right] Qk=[Ik−100Qk′] 这样 Q k Q_k Qk是与 Q 1 Q_1 Q1维度一致的正交矩阵，且能使第 k k k列第 k k k行下方的元素全部归 0 0 0。因此，通过找寻多个这样的 Q Q Q矩阵，我们有： R = Q t ⋯ Q 2 Q 1 A R=Q_{t} \cdots Q_{2} Q_{1} A R=Qt⋯Q2Q1A 那么令 Q = Q t ⋯ Q 2 Q 1 Q=Q_{t} \cdots Q_{2} Q_{1} Q=Qt⋯Q2Q1，这是个正交矩阵。 即可得到QR分解 A = Q R A=QR A=QR。
总结一下，通过Householder变换可以将某个向量变换到 e 1 e_1 e1方向上，从而达到将该向量变成只有1个非零元素的向量，以构造出上三角矩阵。
Givens旋转(变换)另一个非常常用的变换是Givens旋转。Givens旋转矩阵定义如下： G ( i , j , θ ) = [ 1 ⋯ 0 ⋯ 0 ⋯ 0 ⋮ ⋱ ⋮ ⋮ ⋮ 0 ⋯ c ⋯ − s ⋯ 0 ⋮ ⋮ ⋱ ⋮ ⋮ 0 ⋯ s ⋯ c ⋯ 0 ⋮ ⋮ ⋮ ⋱ ⋮ 0 ⋯ 0 ⋯ 0 ⋯ 1 ] G(i, j, \theta)=\left[\begin{array}{ccccccc} 1 & \cdots & 0 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & & \vdots & & \vdots \\ 0 & \cdots & c & \cdots & -s & \cdots & 0 \\ \vdots & & \vdots & \ddots & \vdots & & \vdots \\ 0 & \cdots & s & \cdots & c & \cdots & 0 \\ \vdots & & \vdots & & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & \cdots & 0 & \cdots & 1 \end{array}\right] G(i,j,θ)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1⋮0⋮0⋮0⋯⋱⋯⋯⋯0⋮c⋮s⋮0⋯⋯⋱⋯⋯0⋮−s⋮c⋮0⋯⋯⋯⋱⋯0⋮0⋮0⋮1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤ 对一个矩阵进行Givens变换就是对其左乘 G G G。我们看着这个 G G G矩阵非常吓人，其实完全是纸老虎。不着急，先将 G G G的定义明确，其为: g k k = 1 for k ≠ i , j g k k = c for k = i , j g j i = − g i j = − s \begin{aligned} g_{k k} &=1 & \text { for } k \neq i, j \\ g_{k k} &=c & \text { for } k=i, j \\ g_{j i} &=-g_{i j} =-s \end{aligned} gkkgkkgji=1=c=−gij=−s for k=i,j for k=i,j 注意到， G G G相关的三个参量 i , j , θ i,j,\theta i,j,θ决定了 G G G的具体值。我们可以轻易观察到， G G G其实就是对单位阵进行了4个元素的修改。 具体而言， 给定两个参数 i , j i,j i,j，假设 i > j i>j i>j， 首先将第 i i i个和第 j j j个对角元素值由 1 1 1改为 c c c，然后将第 i i i行 j j j列和第 j j j行 i i i列的元素分别改为 s s s和 − s -s −s。 s s s和 c c c的具体取值则由 θ \theta θ决定，而 θ \theta θ则取决于我们的旋转目的，接下来将详述。
首先注意到，尽管 G G G矩阵的维度很大，但我们不难发现，对矩阵 A A A左乘 G G G，其实只对 A A A矩阵中的第 i i i行和第 j j j行的元素进行了改动，而其他元素都是不变的。 而Givens旋转的意义就在于可以将其中一个元素变为 0 0 0. 具体而言，假如我们期望将第 i i i行的第一个元素变为0， 那么，即： [ c − s s c ] [ a b ] = [ r 0 ] \left[\begin{array}{cc} c & -s \\ s & c \end{array}\right]\left[\begin{array}{l} a \\ b \end{array}\right]=\left[\begin{array}{l} r \\ 0 \end{array}\right] [cs−sc][ab]=[r0] 其中 a a a为第 j j j行的第一个元素， b b b为第 i i i行的第一个元素。因此，我们可以取： r = a 2 + b 2 r=\sqrt{a^{2}+b^{2}} r=a2+b2 和 c ← a / r s ← − b / r \begin{aligned} &c \leftarrow a / r \\ &s \leftarrow-b / r \end{aligned} c←a/rs←−b/r 就可以实现。 我们首先思考一下Givens旋转对应的物理意义：相当于将一个向量(a,b)，旋转到了(r,0)。而 c c c和 − s -s −s分别对应于 cos θ = a / r \cos\theta=a / r cosθ=a/r 和 sin θ = b / r \sin\theta = b / r sinθ=b/r。
因此，我们可以认为Givens旋转是对矩阵中某个 2 × 1 2\times 1 2×1的向量进行角度为 θ \theta θ的旋转，最常用的场景就是将其旋转到 x x x轴上，即使得向量的第二个元素为 0 0 0。
注意到， Givens旋转矩阵 G G G也是正交矩阵。
Givens旋转与QR分解接下来，结合QR分解，通过一个例子来说明Givens旋转的工作方式以加深理解。对于一个给定的 3 × 3 3\times 3 3×3的矩阵如下： A 1 = [ 6 5 0 5 1 4 0 4 3 ] A_{1}=\left[\begin{array}{lll} 6 & 5 & 0 \\ 5 & 1 & 4 \\ 0 & 4 & 3 \end{array}\right] A1=⎣⎡650514043⎦⎤ 我们试图通过Givens旋转将其转化为一个上三角矩阵，从而实现QR分解。 为此，我们需要将(2,1)和(3,2)位置的元素 5 5 5和 4 4 4都化为 0 0 0。 我们首先对 ( 2 , 1 ) (2,1) (2,1)元素进行操作。为此，我们可以取Givens矩阵如下： G 1 = [ c − s 0 s c 0 0 0 1 ] G_{1}=\left[\begin{array}{ccc} c & -s & 0 \\ s & c & 0 \\ 0 & 0 & 1 \end{array}\right] G1=⎣⎡cs0−sc0001⎦⎤ 根据上面的介绍，这里 c c c和 s s s取值分别可以为： r = 6 2 + 5 2 ≈ 7.8102 c = 6 / r ≈ 0.7682 s = − 5 / r ≈ − 0.6402 \begin{aligned} &r=\sqrt{6^{2}+5^{2}} \approx 7.8102 \\ &c=6 / r \approx 0.7682 \\ &s=-5 / r \approx-0.6402 \end{aligned} r=62+52 ≈7.8102c=6/r≈0.7682s=−5/r≈−0.6402 则有： A 2 = G 1 A 1 ≈ [ 7.8102 4.4813 2.5607 0 − 2.4327 3.0729 0 4 3 ] A_2 = G_1A_1\approx\left[\begin{array}{ccc} 7.8102 & 4.4813 & 2.5607 \\ 0 & -2.4327 & 3.0729 \\ 0 & 4 & 3 \end{array}\right] A2=G1A1≈⎣⎡7.8102004.4813−2.432742.56073.07293⎦⎤ 可以看到其实第二列第三列的数字也是变化了的，这是因为Givens旋转是对两行一起生效的。 进一步地，对(3,2)元素的操作，可以选择Given矩阵： G 2 = [ 1 0 0 0 c − s 0 s c ] G_{2}=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & c & -s \\ 0 & s & c \end{array}\right] G2=⎣⎡1000cs0−sc⎦⎤ 其中 r ≈ ( − 2.4327 ) 2 + 4 2 ≈ 4.6817 c ≈ − 2.4327 / r ≈ − 0.5196 s ≈ − 4 / r ≈ − 0.8544. \begin{aligned} &r \approx \sqrt{(-2.4327)^{2}+4^{2}} \approx 4.6817 \\ &c \approx-2.4327 / r \approx-0.5196 \\ &s \approx-4 / r \approx-0.8544 . \end{aligned} r≈(−2.4327)2+42 ≈4.6817c≈−2.4327/r≈−0.5196s≈−4/r≈−0.8544. 可以得到： A 3 = G 2 A 2 ≈ [ 7.8102 4.4813 2.5607 0 4.6817 0.9664 0 0 − 4.1843 ] A_{3} =G_2A_2\approx\left[\begin{array}{ccc} 7.8102 & 4.4813 & 2.5607 \\ 0 & 4.6817 & 0.9664 \\ 0 & 0 & -4.1843 \end{array}\right] A3=G2A2≈⎣⎡7.8102004.48134.681702.56070.9664−4.1843⎦⎤ 因此，我们有： A 3 = G 2 G 1 A 1 → A 1 = G 1 − 1 G 2 − 1 A 3 = G 1 T G 2 T A 3 A_3 = G_2G_1A_1 \rightarrow A_1=G_1^{-1} G_2^{-1}A_3=G_1^TG_2^TA_3 A3=G2G1A1→A1=G1−1G2−1A3=G1TG2TA3
也即， A 1 A_1 A1矩阵的QR分解为， Q = G 1 T G 2 T Q=G_1^TG_2^T Q=G1TG2T, R = A 3 R=A_3 R=A3.
