- 前言
- AOE网
- 事件 V k V_k Vk 的最早发生时间 V e ( K ) Ve(K) Ve(K)
- 事件 V k V_k Vk 的最迟发生事件 V l ( K ) Vl(K) Vl(K)
- 活动 a i a_i ai 的最早开始时间 e ( i ) e(i) e(i)
- 活动 a i a_i ai 的最迟开始时间 l ( i ) l(i) l(i)
- 活动的差额d
- 原理
- 代码实现
在带权有向图中, 以顶点表示 事件 ,以 有向边 表示 活动 ,以 边上的权值 表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动的网络,简称 A O E AOE AOE 网
A O E AOE AOE 网和 A O V AOV AOV 网都是有向无环图,不同之处在于, A O E AOE AOE 网的边有权值,而 A O V AOV AOV 网无权值,仅表示顶点之间的前后关系, A O E AOE AOE 网的两个性质如下:
- ①只有在 某顶点所代表的事件发生后 ,从该顶点出发的各有向边所代表的活动才能开始
- ②只有在进入某顶点的各 有向边 所代表的 活动 都已 结束 时,该顶点所代表的事件才能发生。
注意
- 在 A O E AOE AOE 网中,有些活动是可以并行进行的
- 从源点到汇点的有向路径可能有多条, 并且这些 路径长度 可能不同,因此从源点到汇点中 最大路径长度(即最大边权和) 的路径称为 关键路径 ,关键路径上的活动称为 关键活动 ,显然这个关键路径可能有多条
- 只有 所有路径的活动 都完成,整个工程才算结束
它是指从源点 V 1 V_1 V1 到顶点 V k V_k Vk 的最长路径长度。事件 V k V_k Vk 的最早发生时间决定了所有从 V k V_k Vk 开始的 活动能够开工的 最早时间 。 可用下面的边推公式来计算:
- V e ( 源点 ) = 0 Ve(源点)=0 Ve(源点)=0
- V e ( k ) = M a x V e ( j ) + W e i g h t ( V j , V k ) Ve(k) = Max{Ve(j)+Weight(V_j,V_k)} Ve(k)=MaxVe(j)+Weight(Vj,Vk) ,其中的 V k V_k Vk 为 V j V_j Vj 的任意后继结点, W e i g h t ( V j , V k ) Weight(V_j,V_k) Weight(Vj,Vk) 表示 < V j , V k > 边上的权值
简单理解一下,假设我们当前走到了点 j j j ,然后我们将点 j j j 的所有出度点 k k k 的 V e ( k ) Ve(k) Ve(k) 值和当前 j j j 点的 V e ( j ) Ve(j) Ve(j)加边权 < j , k > 进行比较,如果后者大就更新为后者(就是尽可能让 V e ( k ) Ve(k) Ve(k) 更大),看到这个我们很自然想起了拓扑排序,我们可以再拓扑排序的基础上进行计算
这里说一下为什么称为 最早发生时间 ,毕竟刚接触怎么看都是 “最迟” ,想象一下,这个 A O E AOE AOE 网是从源点出发,可能会存在多个活动并行进行的情况,但目的都是到达汇点,那么在这个过程中,可能通过某些活动(弧)早到,有的活动(弧)晚到,其中最晚到的活动(弧)就是关键活动,对于那些能 “早到” 的路径来说就会存在两个情况,是先完成活动再等待那个所谓的关键活动完成,还是先等待关键活动,然后再完成这个活动,这里先完成当前的活动就是最早发生时间,而等待后再来完成就是一个活动开始最迟时间,很显然 在关键路径上的最早发生时间和最迟发生时间是一样的
事件 V k V_k Vk 的最迟发生事件 V l ( K ) Vl(K) Vl(K)它是指在不推迟整个工程完成的前提下, 即保证它的后继事件 V j V_j Vj 在其最迟发生时间 V l ( j ) Vl(j) Vl(j) 能够 发生时,该事件最迟必须发生的时间 。 可用下面的递推公式来计算:
- V l ( 汇点 ) = V e ( 汇点 ) Vl(汇点)=Ve(汇点) Vl(汇点)=Ve(汇点)
- V l ( k ) = M i n V l ( j ) + W e i g h t ( V k , V j ) Vl(k) = Min{Vl(j) + Weight(V_k,V_j)} Vl(k)=MinVl(j)+Weight(Vk,Vj) ,其中点 V k V_k Vk 为 V j V_j Vj 的任意前驱结点, W e i g h t ( V k , V j ) Weight(V_k,V_j) Weight(Vk,Vj) 表示 < V k , V j > 边上的权值
这里其实和上面流程其实是类似的,只不过需要从汇点出发一直到源点,那么这个很显然就是一个逆拓扑排序的操作,然后不断地尽可能最小化 V l ( k ) Vl(k) Vl(k) 的值,当然对于关键路径上的活动的 V l ( k ) Vl(k) Vl(k) 和 V e ( k ) Ve(k) Ve(k) 是相同的
活动 a i a_i ai 的最早开始时间 e ( i ) e(i) e(i)它是指该活动弧的起点所表示的事件的最早发生时间。若边 < V k , V j > <V_k, V_j> <Vk,Vj> 表示活动 a i a_i ai ,则有 e ( i ) = V e ( k ) e(i) =Ve(k) e(i)=Ve(k)
活动 a i a_i ai 的最迟开始时间 l ( i ) l(i) l(i)它是指该活动弧的终点所表示 事件的最迟发生时间 与该 活动所需时间 之差。若边 < V k , V j > <V_k,V_j> <Vk,Vj> 表示活动 a i a_i ai ,则有 l ( i ) = v l ( j ) − W e i g h t ( V k , V j ) l(i) = vl(j) - Weight(V_k,V_j) l(i)=vl(j)−Weight(Vk,Vj)
活动的差额d它是指该活动完成的时间余量,即在 不增加完成整个工程所需总时间 的情况下,活动 a i a_i ai 可以拖延的时间,若一个活动的时间余量为 0 0 0 则说明这个活动必须要如期完成,否则会延长整个工期,换句话说就是 关键活动 d ( i ) = l ( i ) − e ( i ) d(i) = l(i) - e(i) d(i)=l(i)−e(i)
原理求解关键路径的算法步骤大体为五步:
- ①从源点出友,令 V e ( 源点 ) = 0 Ve(源点) = 0 Ve(源点)=0,按拓扑有序求其余顶点的最早发生时间 V e ( i ) Ve(i) Ve(i)
- ②从汇点出友,令 V i ( 汇点 ) = V e ( 汇点 ) Vi(汇点) = Ve(汇点) Vi(汇点)=Ve(汇点) , 按逆拓拓扑有序求其余顶点的最迟发生时间 V l ( i ) Vl(i) Vl(i)
- ③根据各顶点的 v e ( i ) ve(i) ve(i) 值求所有孤的最早开始时间 e ( i ) e(i) e(i)
- ④根据各顶点的 v l ( i ) vl(i) vl(i) 值求所有孤的最早开始时间 l ( i ) l(i) l(i)
- ⑤求 A O E AOE AOE 网 中所有活动的差额 d ( ) d() d(),找出所有 d ( ) = 0 d() = 0 d()=0 的活动构成关键路径(可能不唯一)
举例: 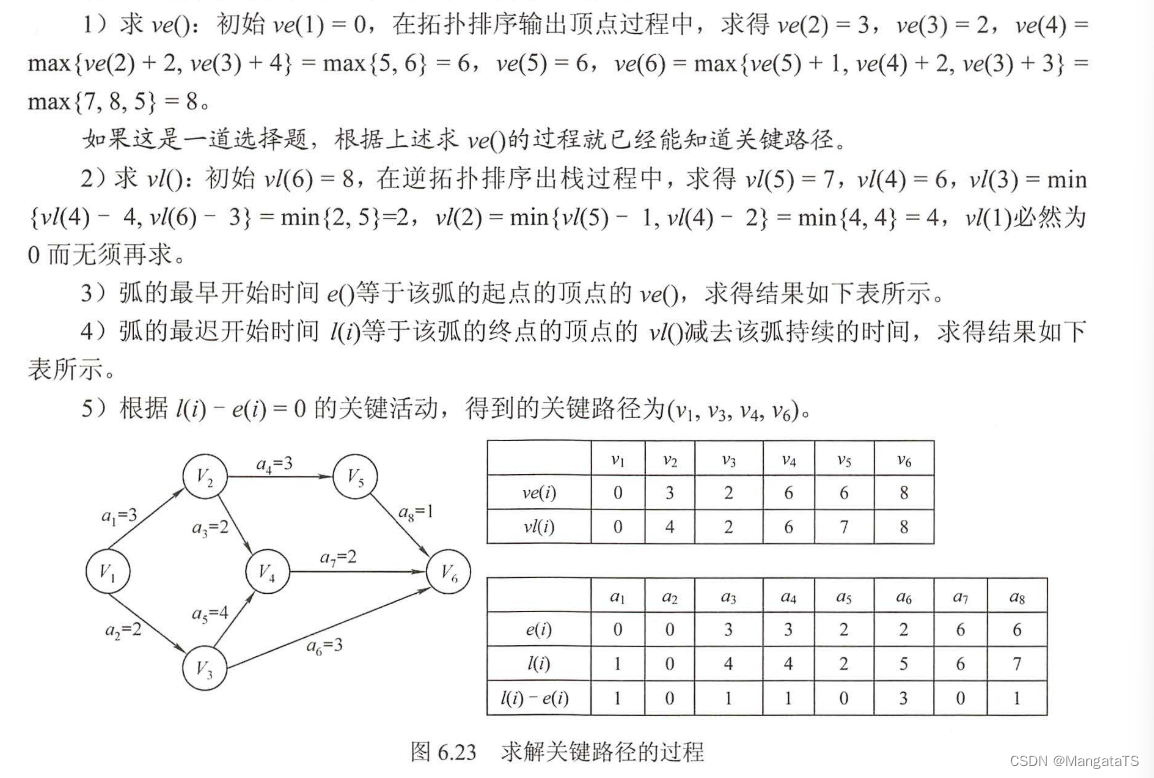
注意: 因为 A O E AOE AOE 网中的关键路径可能不唯一,提高某一个活动的效率可能并不能加快整体工程的效率 关键路径的难点在于理解事件的 最早和最迟时间
代码实现思路较为简单,且未碰到编程类的题目,博主这里就不做实现了,可以参考另一位大佬的实现代码: 博客链接:https://blog.csdn.net/weixin_42638946/article/details/120154312
/*
输出关键路径
input:
9 11
1 2 6
1 3 4
1 4 5
2 5 1
3 5 1
4 6 2
5 7 9
5 8 7
6 8 4
7 9 2
8 9 4
output:
1 2 5 8 9
1 2 5 7 9
*/
#include
#include
#include
using namespace std;
const int N = 1010, M = 100010;
int n, m;
int hs[N], ht[N], e[M], w[M], ne[M], idx; // 顶点表示事件,边表示活动
int ve[N], vl[N]; // 事件允许的最早发生时间, 事件允许的最晚发生时间
// int ee[M], el[M]; // 活动的最早发生时间, 活动的最晚发生时间
int d[N]; // 每个点的入度
int q[N]; // 拓扑排序数组
vector path;
vector res;
void add(int h[], int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void topsort() {
int hh = 0, tt = 0;
q[0] = 1;
while (hh > n >> m;
memset(hs, -1, sizeof hs);
memset(ht, -1, sizeof ht);
for (int i = 0; i > a >> b >> c;
add(hs, a, b, c);
add(ht, b, a, c);
d[b]++;
}
// 输入满足1号点是源点,n号点是汇点
critical_path();
dfs(1);
for (auto &t : res) {
for (int i = 0; i
关注
打赏
最近更新
- 深拷贝和浅拷贝的区别(重点)
- 【Vue】走进Vue框架世界
- 【云服务器】项目部署—搭建网站—vue电商后台管理系统
- 【React介绍】 一文带你深入React
- 【React】React组件实例的三大属性之state,props,refs(你学废了吗)
- 【脚手架VueCLI】从零开始,创建一个VUE项目
- 【React】深入理解React组件生命周期----图文详解(含代码)
- 【React】DOM的Diffing算法是什么?以及DOM中key的作用----经典面试题
- 【React】1_使用React脚手架创建项目步骤--------详解(含项目结构说明)
- 【React】2_如何使用react脚手架写一个简单的页面?



