LeetCode_二叉搜索树_困难_1373.二叉搜索子树的最大键值和

1.题目

给你一棵以 root 为根的 二叉树 ，请你返回任意二叉搜索子树的最大键值和。

二叉搜索树的定义如下： 任意节点的左子树中的键值都小于此节点的键值。 任意节点的右子树中的键值都大于此节点的键值。 任意节点的左子树和右子树都是二叉搜索树。

示例 1：

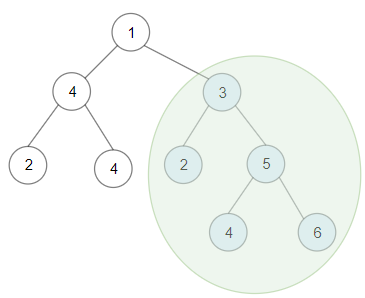
输入：root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6] 输出：20 解释：键值为 3 的子树是和最大的二叉搜索树。

示例 2：

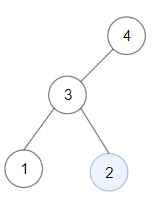
输入：root = [4,3,null,1,2] 输出：2 解释：键值为 2 的单节点子树是和最大的二叉搜索树。

示例 3： 输入：root = [-4,-2,-5] 输出：0 解释：所有节点键值都为负数，和最大的二叉搜索树为空。

示例 4： 输入：root = [2,1,3] 输出：6

示例 5： 输入：root = [5,4,8,3,null,6,3] 输出：7

提示： 每棵树有 1 到 40000 个节点。 每个节点的键值在 [- 4 * 104 , 4 * 104] 之间。

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/maximum-sum-bst-in-binary-tree

2.思路

（1）后序遍历 思路参考美团面试官：你对后序遍历一无所知。

（2）递归 思路参考本题官方题解。

3.代码实现（Java）

//思路1————后序遍历
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

    // res 记录二叉搜索子树的最大键值和
    int maxSum = 0;

    public int maxSumBST(TreeNode root) {
        traverse(root);
        return maxSum;
    }

    /*
        返回值为一个长度为 4 的数组，假设称为 res，其中
        res[0]:记录以 root 为根的二叉树是否是 BST，若为 1 则说明是 BST，否则不是
        res[1]:记录以 root 为根的二叉树所有节点中的最小值
        res[2]:记录以 root 为根的二叉树所有节点中的最大值
        res[3]:记录以 root 为根的二叉树所有节点值之和
    */
    public int[] traverse(TreeNode root) {
        if (root == null) {
            return new int[]{1, Integer.MAX_VALUE, Integer.MIN_VALUE, 0};
        }
        //递归计算左右子树
        int[] left = traverse(root.left);
        int[] right = traverse(root.right);

        int[] res = new int[4];
        //判断以 root 为根的二叉树是否为 BST
        if (left[0] == 1 && right[0] == 1 && root.val > left[2] && root.val  left.maxValue && root.val