- 说在前头
- 证明极限不存在
- 方法
- 格林公式的应用
- 公式形式和条件
- 基本例题1:
- 基本例题2:
- 基本例题3:
- 高斯公式的应用
- 公式形式和条件::
- 基本例题1:
- 基本例题2
- 基本例题3:
- 等比级数
- P级数
- 敛散性的判定
- 区分类型
- 如果是正项级数
- 重要极限:
- 如果是交错级数
- 交错级数收敛的分类
- 绝对收敛
- 条件收敛
- 例题1:
- 例题2:
- 幂级数
- 收敛半径|收敛区间|收敛域
- 幂级数求和函数
- 类型1:
- 类型2:
- 类型3:
[这篇博客的截图全部来自]
如果对于z或者x,y是常数 那么 dx = dy= dz = 0
证明极限不存在(多元函数)
不存在:
若存在两个方向极限不相等则极限不存在
方法取两个满足趋近该点的直线 然后代入看是否相等即可

对于正向的解释,即你绕着边界走 你的左手边要落在区域当中 
最基本的应用没有一点变换
(注意 我们是用 对x偏导 - 对y的偏导 不要弄反)

如果分母 那么我们可以带入进行优化 (这是 点满足在直线上 不深究了 ) 
(添加辅助线计算)
细节1: 最后求积分的时候并没有分 x型y型 而是直接通过二重积分的意义 来直接进行计算了 即m*半圆的面积
细节2: (点在直线上满足直线方程) 所以对于后面计算已经加的曲线的时候直接看出来是0了 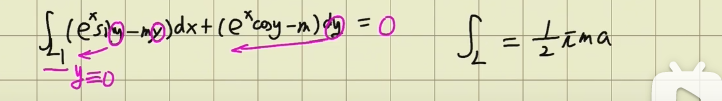 过程图:
过程图:

(用于计算第二类的曲面积分) (每次都是三重积分的计算难到我 了)
公式形式和条件::连续 && 向外流 
转换还是好懂的,但是计算三重积分这里用了 球坐标计算 老师没要求 考不到 算了

添加辅助平面的做法
先计算三重积分
然后再减去原先加上的平面
先将z = 2 带入方程 然后再投影 D 出来
最后判断加的平面方向 是否需要加符号
最后计算即可 
也是加了面 (emm)
这里用的不知道叫什么计算三重积分 但是我会
就是后面单独算这个平面的时候人有点懵
因为他加的这个面是下侧 所以需要加个负号 让我有点没反应过来



先看通向,通向不为0直接发散
区分类型


莱布尼兹法则 递减 -> 则收敛
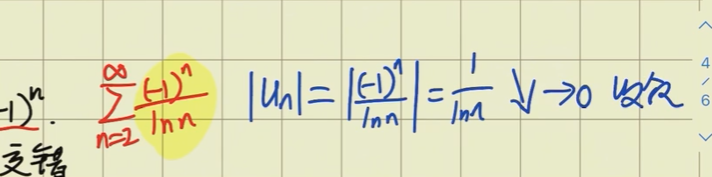
如果|Un|收敛 则Un是绝对收敛的
条件收敛若|Un|发散 但是本身是发散的
例题1:1.打绝对值之后
Un = 1/ln n 发散的
2.但是对于本身
先取绝对值
因为1/ln n 单调 -.> 0
所以本身是收敛的
所以条件收敛 
这里还用了比较审敛法 是我不配了 
R是 收敛半径 收敛区间 是 -R, R 收敛域 要考虑端点 (将端点带入进去 观察是否收敛 收敛则可取) 
(换元法 基本上是将某个看成整体然后直接带入模板里)
类型1: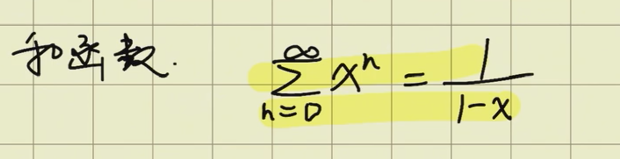
S(x) = -ln(1-x) 、
S= 1/(1-x^2) 



